高数 |
您所在的位置:网站首页 › 对弧长的曲线积分的计算方法证明 › 高数 |
高数
|
前言:本篇讲述第一类曲线积分和第二类曲线积分,以及它们的区别与联系。 目录: 第一类曲线积分——对弧长的曲线积分 1、概念引入 2、定义 3、性质 4、计算 第二类曲线积分——对坐标的曲线积分 1、概念引入 2、定义 3、性质 4、计算 两类曲线积分之间的联系 第一类曲线积分——对弧长的曲线积分 1、概念引入举一个实际生活中的例子: 我们知道有些物体的质量是均匀分布的,比如高中经常用到的“质量均匀分布的小球”这样的理想化模型,但在现实生活中,大部分物体的质量不是均匀分布的。质量不均匀在于密度不均匀,如果物体的密度按照一定的规律变化,就可以将密度的分布情况用函数表示,这样就有了线密度、面密度、体密度等。 对一个弧状的物体(理想化地将其看作一条二维平面上的弧线)而言,算其质量要考虑其线密度。 首先,将一段线密度为f(x,y)的弧分割成n小段。然后用微元的思想,每一小段的密度都是均匀的,所以第i段的质量就为
然后近似求和:
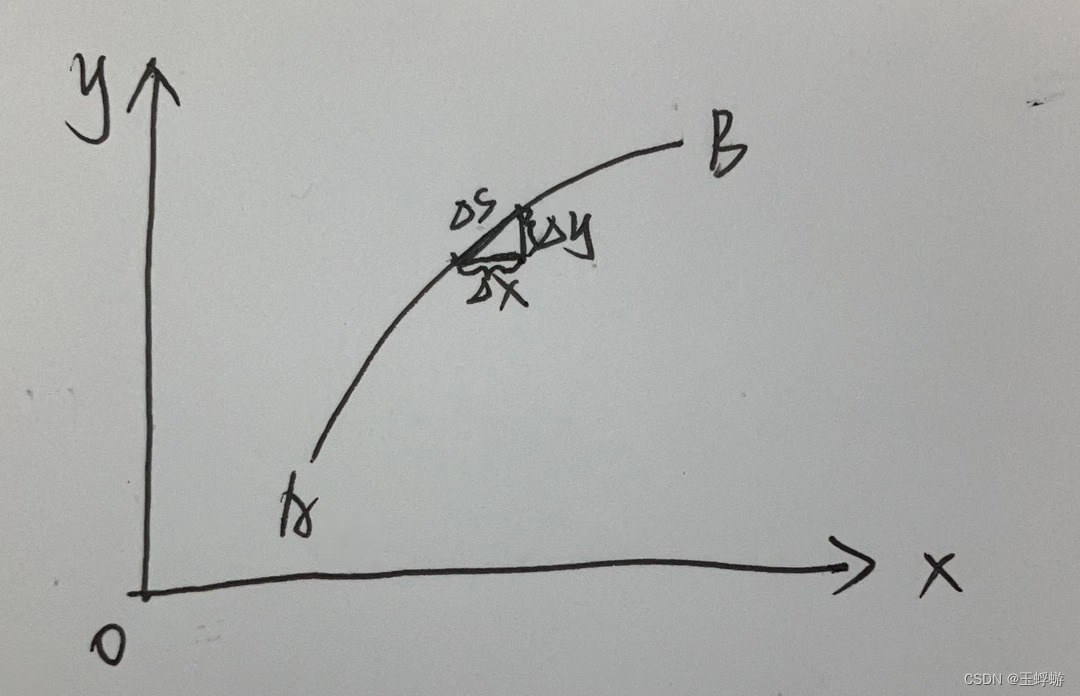
其中,f(x,y)为被积函数,L为积分弧段。即f在一段平面弧上的积分,ds为弧长元素。 类似地,平面弧可以推广到空间弧,设函数为f(x,y,z),曲线弧为Γ,那么函数在空间曲线弧上的积分为 满足线性性,可加性,被积函数为1时几何意义为弧长,保号性,保序性,估值性,中值定理这7个性质,具体的证明就不再多说了。 4、计算不按课本上复杂的证明来理解,这里给出一种较为简单直观的方法。 重点在弧长元素ds,当ds→0时,由微分的思想化曲为直,即一段很小的弧就是一小段直线。为了便于计算,通常将弧向x轴和y轴作垂线,即构成了一个小直角三角形,如图: 即将难以表示的Δs转换成立易于表示的Δx和Δy,即 所以弧长的曲线积分常转化为参数形式来计算,即当参数t由α变为β时
|
【本文地址】
今日新闻 |
推荐新闻 |
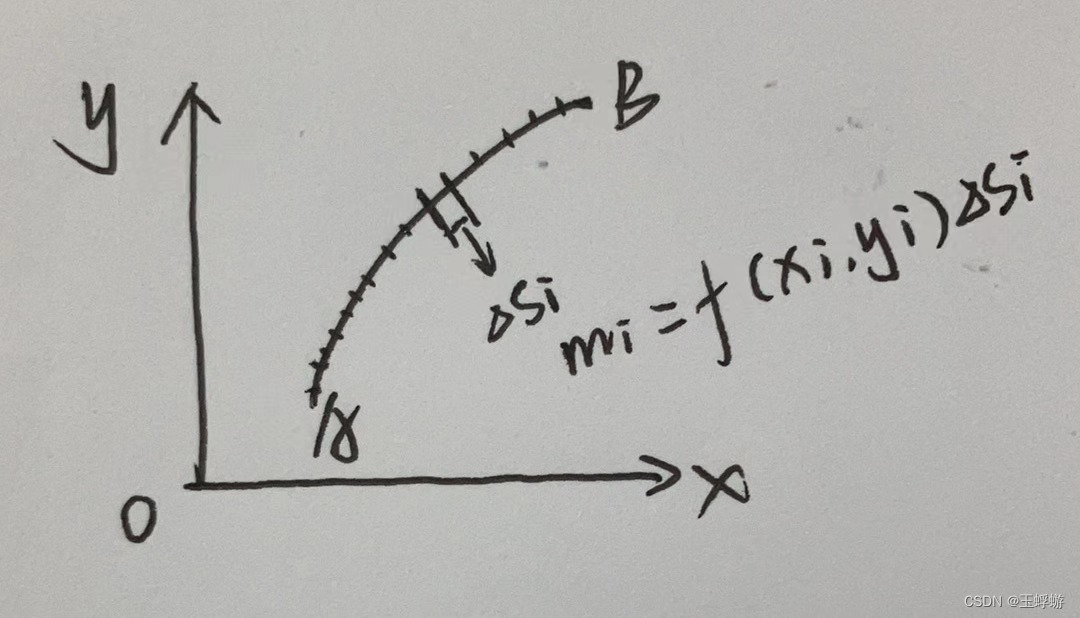
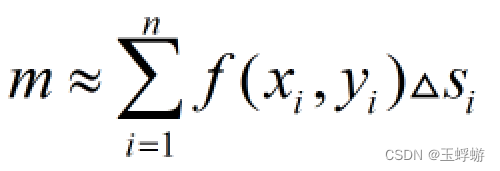 ,最后取极限:取λ为Δsi的最小值,当λ→0,也即每一段弧都趋近于0时,
,最后取极限:取λ为Δsi的最小值,当λ→0,也即每一段弧都趋近于0时,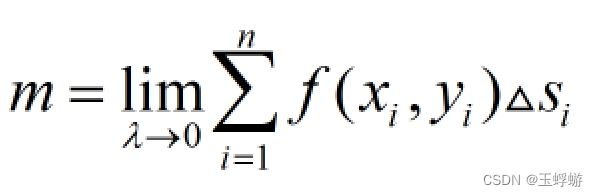 。
。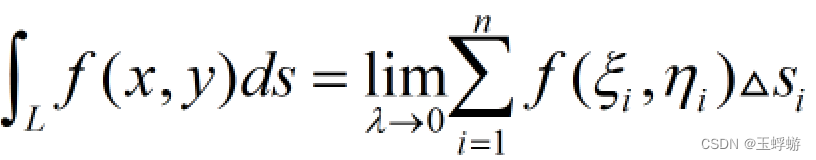
 。
。