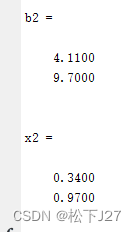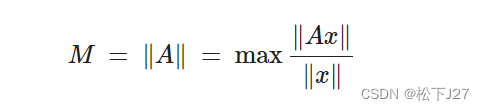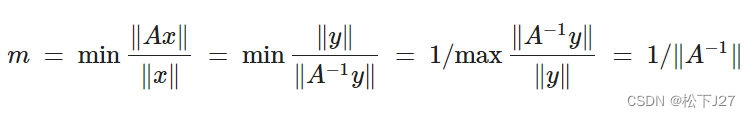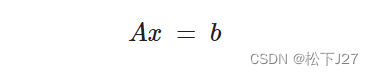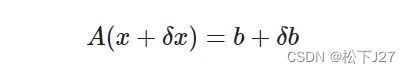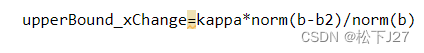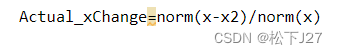在很长的一段时间里，我们判断一个矩阵是否可逆，都是根据矩阵的行列式det是否为0，来判断的。如果行列式的值为0，则我们认定该矩阵为奇异矩阵，即不可逆矩阵。如果行列式的值不为0，则认为该矩阵可逆。

        可实际上，我们在计算机中求矩阵的行列式时，更多时候不太会得到一个标准的0，而是一个很小很小的数，我们会把它当作0，并判断该矩阵不可逆。

        现在我们介绍一种全新的判断矩阵是否可逆的方法，英文叫condition number，中文翻译为条件数。这也是我在matlab里面看到的一个方法，在matlab中的命令为cond(A)。它是方程组Ax=b中右端b的变换对于解x的影响的一个度量值，用希腊字母表示。

我们一起来看下面的这个例子：

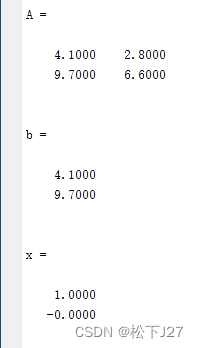
        对于上述方程组Ax=b而言，很明显，等式右端b正好等于A中的第一例。方程有解，说明b在A的列空间中，b等于A中各列的线性组合，x=[1 0]。  

 Matlab code:

 Result:

      现在我们把等式右端b中的第一个值修改0.01，从b=[4.1 9.7]改成b=[4.11 9.7]，然后再重新求解方程。

          奇怪！原来的b等于A的第一例，现在只不过是把b中的第一个数改了0.01，凭直觉，我觉得解x大概率是在[0.99 0]到[1.01 0]之间徘徊吧。因为，毕竟b是A中各列的线性组合，只改了那么一丁点，A中第一列对b的贡献好歹也有99%吧。可是实际结果却让人大跌眼镜，跟我预先的估计完全不一样。（有没有觉得特别像气象学中的蝴蝶效应？）

 Matlab code:

Result:

 引入Condition number条件数(希腊字母kappa)：

         科学家们觉得b的改变对解x的影响存在着一定的关系，并且专门研究了一套度量方法，用于衡量相对于b的改变，方程组的解x的敏感程度(sensitivity)。换句话说就是在研究等式右端b的变化与解x的变化之间的联系，科学家们把这个能够衡量敏感程度的指标用希腊字母表示，它基于对矩阵A的计算，即(A)，MATLAB中的命令为cond(A)。

        在这里，我们先简单的介绍一下如何计算向量的范数，准确的说是计算向量欧几里得范数Euclidean norm或二阶范数2- norm。计算公式为：

  熟悉线性代数的朋友应该发现了，这所谓向量的范数(模)就是n维空间中向量的长度。

        而对于线性方程组Ax=b而言，我们同样也需要考虑矩阵A的范数。矩阵A的范数表示的是矩阵A对向量x的长度改变程度。(友情提示：向量的范数和矩阵的范数的计算方式不同，矩阵的 2-范数为最大奇异值。）

        一方面我们要看看矩阵A最大能把向量x拉的有多长？定义这个最大的拉伸率为M(max)，他等于矩阵A的范数（当A为对称正定矩阵（特征值全为正的对称矩阵），它等于矩阵A的最大特征值，）且有：

        另一方面，我们也要看看矩阵A究竟能把向量x缩的有多小？并定义它为m(min)，即最小拉伸率，它等于矩阵A的逆矩阵的范数的倒数（当A为对称正定矩阵（特征值全为正的对称矩阵），它等于矩阵A的最小特征值的倒数，1/），即：

对于奇异矩阵而言，矩阵不可逆，m=0。

也就是说，如果把Ax看成矩阵A对x的操作，并把b看成A对x操作的结果。那么，根据对于M和m的定义，A对x的操作结果b，也就是向量b的模的变化相对于向量x的变换，最大不会超过M，最小不会小于m。

现在我们可以定义条件数了，它等于矩阵A的最大拉伸率和最小拉伸率的比值：

或

对于第二个式子而言，如果A为奇异矩阵，则他的条件数为无穷大。

若A为对称正定矩阵（特征值全为正的对称矩阵），则：

回到线性方程组的讨论：

        现在我们就详细的考察一下b的变化与x的变化的相对联系，即delta b对delta x的影响。

原方程组为：

结合矩阵A的最大拉伸率M的定义，他代表了矩阵A拉伸\放大一个向量的能力上限。也就是说无论矩阵A对x怎么操作即Ax(在这里是拉伸、放大)，最终得到的结果向量Ax的长度，即||Ax||，不会大于||A||乘以x的长度，即||A|||x||：

也就是说，||A|||x||决定了A对x操作的上限。

又因为Ax=b，Ax的长度等于b的长度：

又最大拉伸率M等于A的模，即M=||A||，所以有：

修改b后的对应方程组为：

        其中就表示b的改变量，而表示的就是相对于原来的解x，当b改变以后，x的变化。用这个方程减去原方程有：

继而有：

或

        再来，结合矩阵A的最小拉伸率m的定义，他代表了矩阵A拉伸\放大一个向量的能力下限。也就是说无论A的逆矩阵对怎么操作即，最终得到的结果向量的长度，即||||，不会小于||||乘以的长度，即|||||||：

 也就是说，|||||b||决定了对b操作的下限。

又因为=，所以有：

又因为最小拉伸率m等于A的逆矩阵的模的倒数，即m=1/||||，所以有：

无论是基于

     和   

还是基于

   和   

利用不等式的同向正值不等式可乘性：如果a>b>0，m>n>0，那么am>bn 

再加上：                                  或  

最终得到：

不等式左边的||δb||/||b||表示的正是方程组右端b的相对变化，不等式右边的||δx||/||x||所表示的也正好是修改b后，方程组的解的相对变化。这个不等式表明： 等式右侧b的相对变化乘以矩阵的条件数(A)为方程组解x的变化的上限。

下面我看看MATLAB的实际情况：

首先我们先来计算条件数，按照定义条件数(A)等于A的范数乘以A的逆的范数.

Matlab code:

 Result:

 又因为A为对称正定矩阵（特征值全为正的对称矩阵），则我们还可以用另外一种基于特征值的算法计算条件数：

Matlab code:

 Result:

首先尝试对矩阵A做Cholesky分解，如果分解失败，则矩阵不是对称正定矩阵。

然后对矩阵A做奇异值分解，然后再用最大特征值除以最小特征值，同样能够算出正确的条件数。

当然你还可以用matlab自带的条件数函数cond(A)来计算条件数，得到的结果和上述两种方法算出来的是一样的：

Matlab code:

 Result: 

其次，根据不等式右边条件数乘以b的相对变换量，得到解x的变换上限：

Matlab code:

 Result:

 然后，我们再看看x相对于b的实际变化：

Matlab code:

  Result:

        可见，x的这一实际改变1.1732基本上也接近了前面算出来的x的变化的上限1.5412。这也正好符合或者说很好的解释了前面的疑惑，为什么b中的一个元素的小小的0.01的改变，彻底的改变了原始方程组的解x。

        总结：b的一小步，x的一大步。x的变化之巨，直接逼近了x的变化上限1.5412，而这一变化上限是基于条件数算出来的，他反应了x对于b的变化的敏感程度。在Matlab的算法中，条件数接近 1 则表示该矩阵为良态矩阵，而条件数越大则说明该矩阵越有可能是病态矩阵，当条件数接近无穷大时Inf时，该矩阵为奇异矩阵。

 （全文完）

作者 --- 松下J27

参考文献（鸣谢）：

1，What is the Condition Number of a Matrix? » Cleve’s Corner: Cleve Moler on Mathematics and Computing - MATLAB & Simulink

2，向量范数和矩阵范数 - MATLAB norm- MathWorks 中国

3，逆运算的条件数 - MATLAB cond- MathWorks 中国

格言摘抄：

有罪的人哪，要洁净你们的手！心怀二意的人哪，要清洁你们的心！-----《圣经，雅各书4章8节》

 （配图与本文无关）

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27