|
目录
前言:
共轭方向法:
共轭方向及其性质:
共轭梯度法:
定理1:
定理2:
收敛性分析:
FR共轭梯度法:
算法步骤:
例题分析:
算法代码:
简便代码:
总结:
前言:
为了克服最速下降法在最优解附近收敛速度变慢和Newton法不具有整体收敛性以及需要计算Hesse矩阵的缺点,一种介于两者之间的方法被提出,这就是共轭方向法。这种方法不仅克服了上述缺点之外,还能保持上述两种方法各自的优点,即收敛性较好,并且可以在有限布内使二次函数达到最优,即具有二次终止性。
共轭方向法:
基本原理:假设 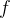 是 n 元正定二次函数 是 n 元正定二次函数  , A 正定,如果按最速下降法,则会发生锯齿现象。希望下次迭代就得到最优解,如果能够选定这样的搜索方向,那么对于二元二次函数,只需沿搜索方向 , A 正定,如果按最速下降法,则会发生锯齿现象。希望下次迭代就得到最优解,如果能够选定这样的搜索方向,那么对于二元二次函数,只需沿搜索方向  进行精确一维搜索就可以求到极小点 进行精确一维搜索就可以求到极小点 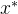 ,即 ,即  。 。
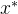 是 是 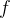 的极小点,故 的极小点,故 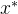 是 是 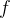 的驻点, 的驻点,




等式两边同时左乘  ,有: ,有:

由于  相互正交,所以相乘为 0, 相互正交,所以相乘为 0,

 是 A 的共轭矩阵 是 A 的共轭矩阵
共轭方向及其性质:
性质1: 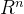 中与 n 个线性无关的向量都正交的一定是零向量。 中与 n 个线性无关的向量都正交的一定是零向量。
性质2: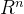 中 A 共轭的非零向量组 中 A 共轭的非零向量组  是线性无关的。 是线性无关的。
性质3: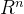 中互相共轭的非零向量的个数不超过 n 。 中互相共轭的非零向量的个数不超过 n 。
性质4:给定 n 元函数  , , 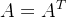 正定,设 n 维非零向量组 正定,设 n 维非零向量组 是 A 共轭向量组,从任意点 是 A 共轭向量组,从任意点 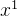 出发,依次以 出发,依次以  为搜索方向进行精确一维搜索,则 为搜索方向进行精确一维搜索,则
(1) 与 与  正交。 正交。
(2)最多 n 次迭代必达到二次函数 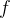 的极小点。 的极小点。
ok,了解了什么是共轭方向法,那接下来我们来看看什么是共轭梯度法!
共轭梯度法:
令 , , 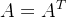 正定, 正定,
(1)从任取初始点 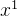 出发,沿负梯度方向进行精确一维搜索: 出发,沿负梯度方向进行精确一维搜索:

(2)若  ,停止,否则在 ,停止,否则在  和 和 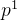 张成的正交锥中找一个向量 张成的正交锥中找一个向量  ,即令 ,即令  ,使得 ,使得


(3)在 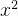 处沿 处沿  方向进行精确一维搜索: 方向进行精确一维搜索:

(4)以此类推;
(5)若  ,停止,否则在 ,停止,否则在  和 和 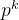 张成的正交锥中找一个向量 张成的正交锥中找一个向量  ,即令 ,即令  ,使得 ,使得 


这样就构造了一组向量组  ,为A的共轭向量组。 ,为A的共轭向量组。
由此,可引申出以下定理。
定理1:
设向量组  是由上述方法产生的向量组,向量组 是由上述方法产生的向量组,向量组  是由各点的梯度生成的向量组 ( 是由各点的梯度生成的向量组 ( ) ,则 ) ,则
(1) 是正交向量组; 是正交向量组;
(2) 是 A 的共轭向量组。 是 A 的共轭向量组。
(注:为保证方向的共轭性,初始方向取负梯度方向)
定理2:
令 , , 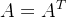 正定,向量组 正定,向量组  是由上述方法构造的 A 的共轭向量组, 是由上述方法构造的 A 的共轭向量组, ,则以下几个计算公式等价: ,则以下几个计算公式等价:
(1) (Daniel共轭梯度法) (Daniel共轭梯度法)
(2) (SW共轭梯度法) (SW共轭梯度法)
(3) (DM共轭梯度法) (DM共轭梯度法)
(4) (FR共轭梯度法) (FR共轭梯度法)
(5) (PPR共轭梯度法) (PPR共轭梯度法)
下面可以用一个反例来理解:
例题:用共轭方向法求下列问题的极值。
 ,已知初始点 ,已知初始点  , , . .
解:
由于初始方向为下降方向,但不是负梯度方向,所得出的  并不是 A 的共轭向量组,导致 n 元二次函数最多 n 次迭代即可达到极小点的结论不成立。 并不是 A 的共轭向量组,导致 n 元二次函数最多 n 次迭代即可达到极小点的结论不成立。
收敛性分析:
设 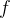 : : 具有一阶连续偏导数, 具有一阶连续偏导数, ,记 ,记  ,假设水平集 ,假设水平集  有界,令 { 有界,令 { } 是由最速下降法产生的点列,则: } 是由最速下降法产生的点列,则:
(1)当 { } 是有穷点列时,其中最后一个点是 } 是有穷点列时,其中最后一个点是 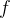 的驻点; 的驻点;
(2)当 { } 是无穷点列时,它必有极限点,并且任一极限点都是 } 是无穷点列时,它必有极限点,并且任一极限点都是 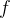 的驻点。 的驻点。
FR共轭梯度法:
FR共轭梯度法是共轭梯度法中最为常见,也是用的最多的一个,那么,下面我们就来展开谈谈FR共轭梯度法的具体做法。
算法步骤:
步骤1:选定初始点 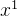
步骤2:如果  ,算法停止, ,算法停止, ,否则转步骤3. ,否则转步骤3.
步骤3:取
步骤4:精确一维搜索找最佳步长 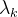 ,令 ,令  . .
步骤5:如果  ,算法停止, ,算法停止, ,否则转步骤6. ,否则转步骤6.
步骤6:如果 k=n ,令 ,转步骤4;否则转步骤7. ,转步骤4;否则转步骤7.
步骤7:计算 , , ,k=k+1,转步骤4. ,k=k+1,转步骤4.
(注:计算过程中存在一定的误差,会使 n 步迭代得不到正定二次函数的极小点,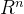 中共轭方向最多有 n 个,n 步后构造的搜索方向不再是共轭的,会大大降低收敛速度,故需要重新开始,将 中共轭方向最多有 n 个,n 步后构造的搜索方向不再是共轭的,会大大降低收敛速度,故需要重新开始,将  作为新的 作为新的 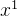 。) 。)
例题分析:
同样的,我们来用一道例题加深对该算法的理解
例题:用 FR 共轭梯度法求  的极小点,已知初始点 的极小点,已知初始点 ,迭代精度 ,迭代精度 =0.001. =0.001.
解:
1)第一次迭代:沿负梯度方向搜索
 , ,


令 


不满足精度,继续迭代。
2)第二次迭代:沿负梯度方向搜索
 , ,


令 


 ,得到最优解 ,得到最优解 
算法代码:
'''
FR共轭方向算法(二元二次函数)
2023.10.20
'''
import numpy as np
from sympy import symbols, diff, solve
x1 = symbols("x1")
x2 = symbols("x2")
λ = symbols("λ")
f = x1 ** 2 + 2 * x2 ** 2 - 4 * x1 - 2 * x1 * x2
def fletcher_reeves(x1_init, x2_init, ε):
# 一阶求导
grad_1 = diff(f, x1)
grad_2 = diff(f, x2)
x1_curr = x1_init
x2_curr = x2_init
first_grad_1_value = grad_1.subs({x1: x1_curr, x2: x2_curr})
first_grad_2_value = grad_2.subs({x1: x1_curr, x2: x2_curr})
g1 = np.array([first_grad_1_value, first_grad_2_value], dtype=float)
norm_result_1 = np.linalg.norm(g1, ord=2, axis=0)
if norm_result_1 |