ベッセルの不等式とその詳しい証明 |
您所在的位置:网站首页 › bessel不等式和parseval等式的区别 › ベッセルの不等式とその詳しい証明 |
ベッセルの不等式とその詳しい証明
|
内積空間におけるベッセルの不等式 (Bessel’s inequality) は, \sum_{n=1}^\infty |\langle x, e_n\rangle |^2\le \| x\| という不等式のことです。それぞれの意味をきちんと説明し,さらにベッセルの不等式を証明しましょう。 ベッセルの不等式とその詳しい証明発展~パーセバルの等式~関連する記事ベッセルの不等式とその詳しい証明以下で, \{ e_n\} が正規直交系 (orthonormal system) であるとは, \langle e_n,e_m\rangle = \begin{cases} 1 & n=m, \\ 0 & n\ne m \end{cases} すなわち,互いに直交する大きさ 1 のベクトルの集まりということです(→正規直交系・正規直交基底)。 定理1(ベッセルの不等式; Bessel’s inequality) X を内積空間, \{e_n\}_{n=1}^\infty\subset X を正規直交系とする。このとき,任意の x\in X に対して, \color{red} \Large \sum_{n=1}^\infty |\langle x, e_n\rangle |^2\le \| x\|が成り立つ。 なお,本定理は \sum_{n=1}^m |\langle x, e_n\rangle |^2\le \| x\| のように左辺が有限和であっても全く同様に成立します。 証明を添付しておきましょう。内積が扱えれば,多くの知識なしで証明可能です。 証明 任意の整数 m\ge 1 に対して, \begin{aligned}0&\le \Bigl\| x-\sum_{n=1}^m \langle x, x_n\rangle e_n \Bigr\|^2 \\ & =\|x\|^2-\Bigl\langle x,\sum_{n=1}^m \langle x, e_n\rangle e_n\Bigr\rangle \\ & \quad -\Bigl\langle \sum_{n=1}^m \langle x, e_n\rangle e_n, x\Bigr\rangle+\Bigl\|\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\| ^2\end{aligned}である。ここで, \begin{aligned}\Bigl\langle x,\sum_{n=1}^m \langle x, e_n\rangle e_n\Bigr\rangle &=\overline{\sum_{n=1}^m \langle x, e_n\rangle } \langle x, e_n\rangle \\ &= \sum_{n=1}^m |\langle x, e_n\rangle|^2,\\ \Bigl\langle \sum_{n=1}^m \langle x, e_n\rangle e_n, x\Bigr\rangle&= \sum_{n=1}^m \langle x,e_n\rangle \langle e_n, x\rangle \\ &= \sum_{n=1}^m |\langle x, e_n\rangle|^2, \\ \Bigl\|\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\| &=\sum_{n=1}^m |\langle x, e_n\rangle|^2 \end{aligned}なので,結局,最初の式は \begin{aligned}0&\le \Bigl\| x-\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\|^2 \\ &= \|x\|^2-\sum_{n=1}^m |\langle x,e_n\rangle|^2 \end{aligned}となる。したがって, \sum_{n=1}^m |\langle x,e_n\rangle|^2\le \|x\|^2 であり,m\to\infty とすることで, \sum_{n=1}^\infty |\langle x,e_n\rangle|^2\le \|x\|^2 である。 証明終 発展~パーセバルの等式~完備な内積空間であるヒルベルト空間においては,もう一段「強い」定理が成立します。以下で, \{ e_n\} が正規直交基底 (orthonormal basis) であるとは, \{e_n\} が正規直交系かつ \overline{\operatorname{Span} \{e_n\}} が空間全体となることを言います(→正規直交系・正規直交基底)。 定理2(パーセバルの等式; Parseval’s equality) H をヒルベルト空間, \{e_n\}_{n=1}^\infty\subset H を正規直交基底とする。このとき,任意の x\in H に対して, \color{red} \Large \sum_{n=1}^\infty |\langle x, e_n\rangle |^2= \| x\|が成り立つ。 これは,三平方の定理(ピタゴラスの定理)の無限次元バージョンということができます。 この定理の証明は,ヒルベルト空間における正射影の話が必要であり,難易度が少々上がります。証明は以下で行っています。 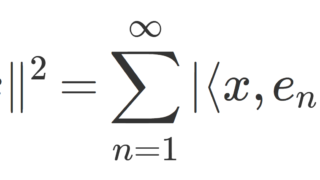 パーセバルの等式とその周辺パーセバルの等式 (Parseval's identity) とは,無限次元のピタゴラスの定理(三平方の定理)といえる定理です。パーセバルの等式について,その形とその証明を行います。また,フーリエ級数におけるパーセバルの等式はよく使われるため,最後に紹介します。 パーセバルの等式とその周辺パーセバルの等式 (Parseval's identity) とは,無限次元のピタゴラスの定理(三平方の定理)といえる定理です。パーセバルの等式について,その形とその証明を行います。また,フーリエ級数におけるパーセバルの等式はよく使われるため,最後に紹介します。ただ,この定理と正射影の話を既知とすると,ヒルベルト空間におけるベッセルの不等式はパーセバルの等式の劣化版ともいえる公式です。実際,正規直交系 \{e_n\} のなす閉部分空間 を L=\overline{\operatorname{Span}\{e_n\}} とし, x\in H の L への正射影を x_L とかくとすると, \begin{equation}\|x_L\|\le \|x\| \end{equation}ですが,パーセバルの等式より, \|x_L\| = \sum_{n=1}^\infty |\langle x, e_n\rangle |^2 なので,結局ベッセルの不等式 \sum_{n=1}^\infty |\langle x, e_n\rangle |^2\le \|x\|が証明できたことになります。結局,ベッセルの不等式は,単に正射影したベクトルのノルムの方が,元のノルムより小さいよ( (1) 式で解釈)と言っているに過ぎません。 ただし,パーセバルの等式の証明には,ベッセルの不等式が必要ですから,「ベッセルの不等式が要らない定理だ」というわけではありません。 関連する記事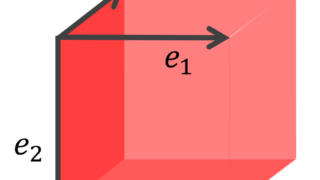 正規直交系・正規直交基底正規直交系とは,大きさが1であり,互いに直交するベクトルの集まりを指します。また,正規直交基底(完全正規直交系)とは,正規直交系で,かつ全てのベクトルがそれらを用いて表現可能なことをいいます。正規直交系・正規直交基底について,定義と具体例を見ていきましょう。 正規直交系・正規直交基底正規直交系とは,大きさが1であり,互いに直交するベクトルの集まりを指します。また,正規直交基底(完全正規直交系)とは,正規直交系で,かつ全てのベクトルがそれらを用いて表現可能なことをいいます。正規直交系・正規直交基底について,定義と具体例を見ていきましょう。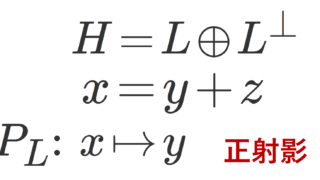 ヒルベルト空間における正射影・正射影作用素ヒルベルト空間における正射影(projection)あるいは直交射影について,その定義を紹介し,関連して正規直交系が与えられた部分空間上への射影について考えましょう。 ヒルベルト空間における正射影・正射影作用素ヒルベルト空間における正射影(projection)あるいは直交射影について,その定義を紹介し,関連して正規直交系が与えられた部分空間上への射影について考えましょう。 |
【本文地址】