数学建模(4):动态规划 |
您所在的位置:网站首页 › 规划求解数学建模步骤 › 数学建模(4):动态规划 |
数学建模(4):动态规划
|
动态规划本身并不是类似前三篇文章所说明的一样,是一种规定的算法,而更像是考察问题的一种途径。自问世以来,它在经济管理、生产调度、工程技术和优控制等方面得到了广泛的应用。例如短路线、库存管理、资源分配、设备更新、排序、装载等问题,用动态规划方法比用其它方法求解更为方便。 §1 动态规划模型的要素动态规划模型的要素是对问题解决的抽象,其可分为: 阶段。指对问题进行解决的自然划分。例如:在最短线路问题中,每进行走一步的决策就是一个阶段。状态。指一个阶段开始时的自然状况。例如:在最短线路问题中,每进行走一步后,对所走的点进行标注。决策。当一个阶段的状态确定后,作出选择从而演变到下一阶段的某个状态的选择手段称为决策,在优控制问题中也称为控制。策略。由决策组成的序列称为策略。由第k到第j阶段的策略可记作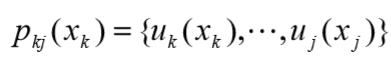 状态转移。 状态转移。  指标函数。用以衡量过程的优劣。 指标函数。用以衡量过程的优劣。  最优策略。对于使指标函数Vk,n达到最优值的策略,我们称之为子过程的最优策略。同样的,我们还有全程的最优策略。递归方程。每一次最优化的求解都是相同原理的机械过程,我们利用计算机辅助计算时可以视其为递归过程。其中: 最优策略。对于使指标函数Vk,n达到最优值的策略,我们称之为子过程的最优策略。同样的,我们还有全程的最优策略。递归方程。每一次最优化的求解都是相同原理的机械过程,我们利用计算机辅助计算时可以视其为递归过程。其中: 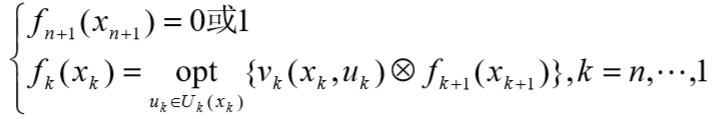 为递归方程。 为递归方程。
纵上所述,如果一个问题能用动态规划方法求解,那么,我们可以按下列步骤,建立起动态规划的数学模型: 1.将过程划分成恰当的阶段 2.正确选择状态变量,使它既能描述过程的状态,又满足无后效性,同时确定允许状态集合 3.选择决策变量 k u 4.写出状态转移方程。 5.确定阶段指标及指标函数的形式(阶段指标之和,阶段指标之积,阶段指标之极大或极小等) 6.写出基本方程即优值函数满足的递归方程,以及端点条件 例如最短线路问题可以使用lingo建模并给出解答 model: Title Dynamic Programming; sets: vertex/A,B1,B2,C1,C2,C3,C4,D1,D2,D3,E1,E2,E3,F1,F2,G/:L; road(vertex,vertex)/A B1,A B2,B1 C1,B1 C2,B1 c3,B2 C2,B2 C3,B2 C4, C1 D1,C1 D2,C2 D1,C2 D2,C3 D2,C3 D3, C4 D2,C4 D3, D1 E1,D1 E2,D2 E2,D2 E3, D3 E2,D3 E3, E1 F1,E1 F2,E2 F1,E2 F2, E3 F1,E3 F2,F1 G,F2 G/:D; endsets data: D=5 3 1 3 6 8 7 6 6 8 3 5 3 3 8 4 2 2 1 2 3 3 3 5 5 2 6 6 4 3; L=0,,,,,,,,,,,,,,,; enddata @for(vertex(i)|i#GT#1:L(i)=@min(road(j,i):L(j)+D(j,i))); end §2 动态规划与静态规划之间的关系动态规划可以看作求决策使指标函数达到最优 (大或小)的极值问题,状态转移方程、端点条件以及允许状态集、允许决策集等是约束条件,原则上可以用非线性规划方法求解。 一些静态规划只要适当引入阶段变量、状态、决策等就可以用动态规划方法求解。 下面用例子说明。 状态转移方程为: 状态转移方程为:
|
【本文地址】
今日新闻 |
推荐新闻 |

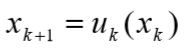 阶段指标为两点距离,指标函数为走过的总距离,最优值函数为由起点到终点的最短距离,且为:
阶段指标为两点距离,指标函数为走过的总距离,最优值函数为由起点到终点的最短距离,且为: 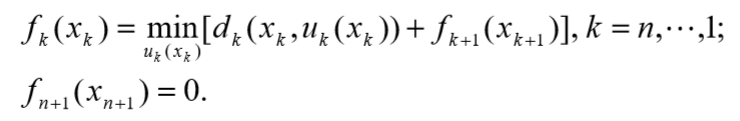
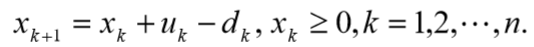 阶段指标为阶段的生产成本和储存费之和
阶段指标为阶段的生产成本和储存费之和 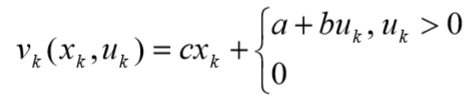 指标函数为阶段指标之和,最优值函数为由起点至完成既定目标的最小费用,且为:
指标函数为阶段指标之和,最优值函数为由起点至完成既定目标的最小费用,且为: