数学建模之规划2 |
您所在的位置：网站首页 › 01规划数学建模经典例题 › 数学建模之规划2 |
数学建模之规划2
|
术语解释
整数规划：规划中的变量（全部或部分）限制为整数，称为整数规划。（很多的单位是不能拆分成小数的）0-1规划：决策变量仅取值0或1的异类特殊的整数规划。（决策变量要么取0，要么取1）（可以解决快递员问题、协作效率最优化问题、解决流程化问题效果很多好）非线性规划：目标函数或约束条件中至少有一个是非线性函数的最优化问题。多目标规划：研究多于一个目标函数在给定区域上的最优化。动态规划：是运筹学的一个分支，是求解决策过程最优化的数学方法。
整数规划及0-1规划模型
概述
首先0-1其实也是整数规划。整数规划指的是决策变量为非负整数值的一类线性规划。在实际问题的应用中，整数规划模型对应着大量的生产计划或活动安排等决策问题，整数规划的解法主要有分枝定界解法及割平面解法。在整数规划问题中，0-1型整数规划则是其中较为特殊的一类情况，它要求决策变量的取值仅为0或1，在实际问题的讨论中，0-1型整数规划模型也对应着大量的最优决策的活动与安排讨论，我们将列举一些模型范例，以说明这个事实。
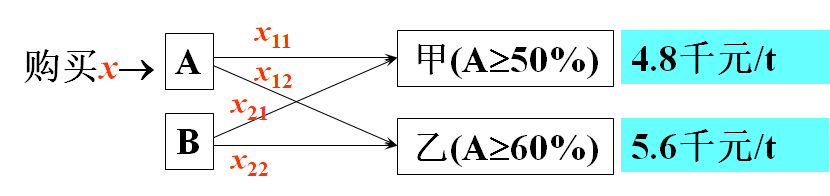
例题1：原油采购与加工
M
a
x
=
4.8
(
x
11
+
x
21
)
+
5.6
(
x
12
+
x
22
)
−
c
(
x
)
Max \space \space = 4.8(x_{11}+x_{21})+5.6(x_{12}+x_{22})-c(x)
Max =4.8(x11+x21)+5.6(x12+x22)−c(x)c(x)~购买原油A的支出
c
(
x
)
=
{
10
x
(
0
≤
x
≤
500
)
8
x
+
1000
(
500
≤
x
≤
1000
)
6
x
+
3000
(
1000
≤
x
≤
1500
)
c(x) = \begin{cases} 10x;(0\leq x\leq 500)\\8x+1000;(500\leq x\leq 1000)\\ 6x+3000;(1000\leq x \leq 1500)\end{cases}
c(x)=⎩⎪⎨⎪⎧10x8x+10006x+3000(0≤x≤500)(500≤x≤1000)(1000≤x≤1500)原油供应
x
11
+
x
12
≤
500
+
x
x_{11}+x_{12}\leq 500+x
x11+x12≤500+x 库存500t
x
21
+
x
22
≤
1000
x_{21}+x_{22}\leq 1000
x21+x22≤1000 库存1000t
x
≤
1500
x\leq 1500
x≤1500不能卖超过1500
x
11
x
11
+
x
21
≥
0.5
\frac{x_{11}}{x_{11}+x_{21}}\geq 0.5
x11+x21x11≥0.5，A要大于50%。
x
12
x
12
+
x
22
≥
0.6
\frac{x_{12}}{x_{12}+x_{22}}\geq 0.6
x12+x22x12≥0.6，B要大于60%。目标函数c(x)不是线性函数，是非线性规划。对于用分段函数定义的c(x)，一般的非线性规划软件也难以输入和求解。
模型求解
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3以价格10，8，6（千元/t）采购A的吨数。这对于任何一种情况都成立。于是有
x
=
x
1
+
x
2
+
x
3
,
c
(
x
)
=
10
x
1
+
8
x
2
+
6
x
3
x = x_1+x_2+x_3,\space c(x) = 10x_1+8x_2+6x_3
x=x1+x2+x3, c(x)=10x1+8x2+6x3
M
a
x
=
4.8
(
x
11
+
x
21
)
+
5.6
(
x
12
+
x
22
)
−
10
x
1
+
8
x
2
+
6
x
3
Max \space \space = 4.8(x_{11}+x_{21})+5.6(x_{12}+x_{22})-10x_1+8x_2+6x_3
Max =4.8(x11+x21)+5.6(x12+x22)−10x1+8x2+6x3然而只有当
x
1
=
500
x_1 = 500
x1=500的时候，
x
2
x_2
x2才能有值，同理当
x
1
+
x
2
≥
1000
x
2
=
500
x_1+x_2\geq 1000 x_2=500
x1+x2≥1000x2=500时，
x
3
x_3
x3才能有值所以约束等价于
(
x
1
−
500
)
∗
x
2
=
0
(x_1-500)*x_2 = 0
(x1−500)∗x2=0【这个太牛逼了】同理
(
x
2
−
500
)
x
3
=
0
(x_2-500)x_3 = 0
(x2−500)x3=0
0
≤
x
1
,
x
2
,
x
3
≤
500
0\leq x_1,x_2, x_3\leq 500
0≤x1,x2,x3≤500
求解代码
Model:
Max= 4.8*x11 + 4.8*x21 + 5.6*x12 + 5.6*x22 - 10*x1 - 8*x2 - 6*x3;
x11+x12 < x + 500;
x21+x22 < 1000;
x11 - x21 > 0;
2*x12 - 3*x22 > 0;
x=x1+x2+x3;
(x1 - 500) * x2=0;
(x2 - 500) * x3=0;
x1 < 500;
x2 < 500;
x3 < 500;
end
最终结果
Local optimal solution found.
Objective value: 4800.000
Total solver iterations: 14
Variable Value Reduced Cost
X11 500.0000 0.000000
X21 500.0000 0.000000
X12 0.000000 0.2666667
X22 0.000000 0.000000
X1 0.000000 0.4000000
X2 0.000000 0.000000
X3 0.000000 0.000000
X 0.000000 0.000000
这里分段函数的处理非常经典，需要反复仔细看。 分派问题（0-1规划） 若干项任务分给一些候选人来完成，每人的专长不同,完成每项任务取得的效益或需要的资源不同，如何分派任务使获得的总效益最大，或付出的总资源最少?若干种策略供选择，不同的策略得到的收益或付出的成本不同，各个策略之间有相互制约关系，如何在满足一定条件下作出抉择，使得收益最大或成本最小?指派(Assignment)问题：有若干项任务, 每项任务必有且只能有一人承担，每人只能承担一项，不同人员承担不同任务的效益(或成本)不同，怎样分派各项任务使总效益最大(或总成本最小)?一般情况分为三种 人员数量与任务数量相等人员数量大于任务数量(本例)人员数量小于任务数量 ? 0-1规划数学模型M a x ( M i n ) z = c 1 x 1 + x 2 x 2 + . . . . . + c n x n Max(Min)z = c_1x_1+x_2x_2+.....+c_nx_n Max(Min)z=c1x1+x2x2+.....+cnxn { a 11 x 1 + a 12 x 2 + . . . a 1 n x n ≤ ( ≥ , = ) b 1 a 21 x 1 + a 22 x 2 + . . . a 2 n x n ≤ ( ≥ , = ) b 2 . . . . . . . . . . . . . . a m 1 x 1 + a m 2 x 2 + . . . a m n x n ≤ ( ≥ , = ) b 2 x 1 , x 2 , . . . . . . , x n = 0 ∣ 1 \begin{cases} a_{11}x_1+a_{12}x_2+...a_{1n}x_n\leq (\geq ,=)b_1 \\a_{21}x_1+a_{22}x_2+...a_{2n}x_n\leq (\geq ,=)b_2 \\.............. \\a_{m1}x_1+a_{m2}x_2+...a_{mn}x_n\leq (\geq ,=)b_2 \\x_1,x_2,......,x_n = 0|1\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧a11x1+a12x2+...a1nxn≤(≥,=)b1a21x1+a22x2+...a2nxn≤(≥,=)b2..............am1x1+am2x2+...amnxn≤(≥,=)b2x1,x2,......,xn=0∣1 案例：混合泳接力队的选拔
 若选择队员i参加泳姿j的比赛，记
x
i
j
=
1
x_{ij} = 1
xij=1，否则记
x
i
j
=
0
x_{ij} = 0
xij=0。这里面的约束相当复杂，队员只能游一种泳姿，并且每种泳姿也只能由一名队员游。目标函数：
m
i
n
Z
=
∑
j
=
1
4
∑
i
=
1
5
c
i
j
x
i
j
min\space Z = \sum^4_{j=1}\sum^5_{i=1}c_{ij}x_{ij}
min Z=j=1∑4i=1∑5cijxij约束条件：
∑
j
=
1
4
x
i
j
≤
1
,
i
=
1
,
.
.
.
,
5
（
1
）
\sum^4_{j=1}x_{ij}\leq 1,i = 1,...,5 \space \space \space \space \space \space \space \space \space \space \space \space \space （1）
j=1∑4xij≤1,i=1,...,5 （1）
∑
i
=
1
5
x
i
j
=
1
,
j
=
1
,
.
.
.
,
4
（
2
）
\sum^5_{i=1}x_{ij} = 1,j = 1,...,4\space \space \space \space \space \space \space \space \space \space \space \space \space （2）
i=1∑5xij=1,j=1,...,4 （2）一式：每人最多入选泳姿。二式：每种泳姿有且只有一个人。
模型求解代码Lingo
MODEL:
sets:
person/1..5/;
position/1..4/;
link(person,position): c, x;
endsets
data:
c= 66.8, 75.6, 87, 58.6,
57.2, 66, 66.4, 53,
78, 67.8, 84.6, 59.4,
70, 74.2, 69.6, 57.2,
67.4, 71, 83.8, 62.4;
enddata
min=@sum(link: c*x);
@for(person(i):
@sum(position(j):x(i,j)) |
目标：你现在要使收益最大，如何安排原油的采购和加工。
【本文地址】
今日新闻 |
推荐新闻 |