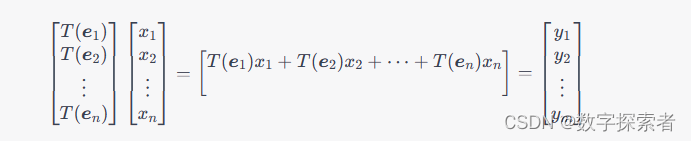线性代数基础

2024-05-24 15:19| 来源: 网络整理| 查看: 265

一、向量的基本概念 A. 向量的定义

向量是数学中的一个基本概念，它表示在空间中具有大小和方向的量。向量可以用箭头来表示，箭头的长度表示向量的大小（模），箭头的方向表示向量的方向。

在坐标系中，向量通常表示为有序数对 ( x , y ) (x,y) (x,y) 或有序三元组 ( x , y , z ) (x,y,z) (x,y,z)，其中 x , y , z x, y, z x,y,z 分别表示向量在 x x x 轴、 y y y 轴、 z z z 轴方向上的大小，也称为向量的分量。向量的长度（模）表示为 ∣ v ∣ |\boldsymbol{v}| ∣v∣，其中 v \boldsymbol{v} v 表示向量。

例如，在二维坐标系中，一个向量 v \boldsymbol{v} v 可以表示为 ( x , y ) (x,y) (x,y) 或 v = x i + y j \boldsymbol{v} = x\boldsymbol{i} + y\boldsymbol{j} v=xi+yj，其中 i \boldsymbol{i} i 和 j \boldsymbol{j} j 分别表示 x x x 轴和 y y y 轴正方向的单位向量。

需要注意的是，向量和标量（单个数值）是不同的概念。标量只有大小，而向量有大小和方向。

B. 向量的表示方法

向量有多种表示方法，其中比较常见的有以下几种：

坐标表示法：向量在坐标系中可以表示为一个有序数对、有序三元组等，其中每个分量表示向量在坐标系的各个方向上的大小。箭头表示法：向量可以用箭头来表示，箭头的长度表示向量的大小（模），箭头的方向表示向量的方向。线段表示法：向量也可以表示为起点和终点之间的有向线段，起点表示向量的位置，线段的方向和长度分别表示向量的方向和大小。分解表示法：向量可以分解为若干个基向量的线性组合，其中基向量是指在坐标系中与坐标轴正方向重合的单位向量。矩阵表示法：向量可以表示为一个列向量或行向量的形式，其中列向量是一个 n n n 行 1 1 1 列的矩阵，行向量是一个 1 1 1 行 n n n 列的矩阵。

在机器学习中，通常使用矩阵表示法来表示向量，因为矩阵具有更好的运算性质。同时，基向量的线性组合也是机器学习中常见的概念，例如，多元线性回归中就是使用基向量的线性组合来表示数据。

C. 向量的加法和减法

向量的加法和减法是向量运算中的基本操作，它们的定义如下：

设 a \boldsymbol{a} a 和 b \boldsymbol{b} b 是两个向量，则它们的和 a + b \boldsymbol{a}+\boldsymbol{b} a+b 和差 a − b \boldsymbol{a}-\boldsymbol{b} a−b 分别定义为：

a + b = ( a 1 + b 1 , a 2 + b 2 , ⋯ , a n + b n ) a − b = ( a 1 − b 1 , a 2 − b 2 , ⋯ , a n − b n ) \begin{aligned} \boldsymbol{a}+\boldsymbol{b} &= (a_1+b_1, a_2+b_2, \cdots, a_n+b_n) \\ \boldsymbol{a}-\boldsymbol{b} &= (a_1-b_1, a_2-b_2, \cdots, a_n-b_n) \end{aligned} a+ba−b=(a1+b1,a2+b2,⋯,an+bn)=(a1−b1,a2−b2,⋯,an−bn)

其中 a i a_i ai 和 b i b_i bi 分别表示向量 a \boldsymbol{a} a 和 b \boldsymbol{b} b 在第 i i i 个方向上的分量， n n n 表示向量的维度。需要注意的是，向量加法和减法要求两个向量具有相同的维度。

图示来看，向量加法和减法的几何意义如下：

向量加法：将一个向量平移后叠加在另一个向量上，得到一个新的向量。向量减法：将一个向量平移后以另一个向量的相反方向叠加在另一个向量上，得到一个新的向量。

可以使用坐标表示法或箭头表示法来表示向量加法和减法。例如，在二维坐标系中，设向量 a = ( a 1 , a 2 ) \boldsymbol{a}=(a_1,a_2) a=(a1,a2)，向量 b = ( b 1 , b 2 ) \boldsymbol{b}=(b_1,b_2) b=(b1,b2)，则它们的和可以表示为 a + b = ( a 1 + b 1 , a 2 + b 2 ) \boldsymbol{a}+\boldsymbol{b}=(a_1+b_1, a_2+b_2) a+b=(a1+b1,a2+b2)，在坐标系中表示为将向量 b \boldsymbol{b} b 平移后叠加在向量 a \boldsymbol{a} a 上得到的新向量。向量的减法可以表示为 a − b = a + ( − b ) \boldsymbol{a}-\boldsymbol{b}=\boldsymbol{a}+(-\boldsymbol{b}) a−b=a+(−b)，其中 − b -\boldsymbol{b} −b 表示向量 b \boldsymbol{b} b 的相反向量。

B. 向量的数量积和向量积

向量的数量积和向量积是向量运算中的两种常见操作，它们分别表示为：

向量的数量积：也称为点积或内积，表示为 a ⋅ b \boldsymbol{a}\cdot\boldsymbol{b} a⋅b，定义为：

a ⋅ b = a 1 b 1 + a 2 b 2 + ⋯ + a n b n = ∑ i = 1 n a i b i \boldsymbol{a}\cdot\boldsymbol{b} = a_1b_1+a_2b_2+\cdots+a_nb_n = \sum_{i=1}^na_ib_i a⋅b=a1b1+a2b2+⋯+anbn=i=1∑naibi

其中 a i a_i ai 和 b i b_i bi 分别表示向量 a \boldsymbol{a} a 和 b \boldsymbol{b} b 在第 i i i 个方向上的分量， n n n 表示向量的维度。向量的数量积是一个标量，表示为两个向量在空间中的夹角的余弦值乘上它们的模长之积，即 a ⋅ b = ∣ a ∣ ∣ b ∣ cos ⁡ θ \boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|\cos\theta a⋅b=∣a∣∣b∣cosθ，其中 θ \theta θ 表示 a \boldsymbol{a} a 和 b \boldsymbol{b} b 之间的夹角。

向量的向量积：也称为叉积或外积，表示为 a × b \boldsymbol{a}\times\boldsymbol{b} a×b，定义为：

a × b = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ = ( a 2 b 3 − a 3 b 2 ) i + ( a 3 b 1 − a 1 b 3 ) j + ( a 1 b 2 − a 2 b 1 ) k \boldsymbol{a}\times\boldsymbol{b} = \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{vmatrix} = (a_2b_3-a_3b_2)\boldsymbol{i}+(a_3b_1-a_1b_3)\boldsymbol{j}+(a_1b_2-a_2b_1)\boldsymbol{k} a×b= ia1b1ja2b2ka3b3 =(a2b3−a3b2)i+(a3b1−a1b3)j+(a1b2−a2b1)k

其中 i \boldsymbol{i} i， j \boldsymbol{j} j 和 k \boldsymbol{k} k 分别表示坐标系的三个基向量， a i a_i ai 和 b i b_i bi 分别表示向量 a \boldsymbol{a} a 和 b \boldsymbol{b} b 在第 i i i 个方向上的分量， 3 3 3 表示向量的维度。向量的向量积是一个向量，其方向垂直于向量 a \boldsymbol{a} a 和 b \boldsymbol{b} b 所在的平面，其大小等于两个向量构成的平行四边形的面积。

需要注意的是，向量的数量积和向量积只能在三维及以上的空间中进行定义，而在二维空间中不存在向量的向量积。此外，向量的数量积和向量积的运算法则具有一定的几何意义，在许多应用中都有着重要的作用。

D. 向量的模和方向角

向量的模和方向角是描述向量的两个重要属性，它们分别表示为：

向量的模：向量的模也称为向量的长度，表示为 ∣ a ∣ |\boldsymbol{a}| ∣a∣，定义为：

∣ a ∣ = a 1 2 + a 2 2 + ⋯ + a n 2 = ∑ i = 1 n a i 2 |\boldsymbol{a}| = \sqrt{a_1^2+a_2^2+\cdots+a_n^2} = \sqrt{\sum_{i=1}^na_i^2} ∣a∣=a12+a22+⋯+an2 =i=1∑nai2

其中 a i a_i ai 表示向量 a \boldsymbol{a} a 在第 i i i 个方向上的分量， n n n 表示向量的维度。向量的模是一个标量，表示向量的大小或长度。

向量的方向角：向量的方向角表示向量与某个坐标轴或平面之间的夹角，通常用极角（也称为极角）和方位角（也称为方向角）表示。在二维直角坐标系中，向量的方向角等于向量与 x x x 轴之间的夹角，可以表示为 θ = arctan ⁡ y x \theta=\arctan\frac{y}{x} θ=arctanxy。在三维直角坐标系中，向量的方向角可以用极角和方位角表示。其中，极角表示向量与 z z z 轴之间的夹角，通常用 ϕ \phi ϕ 表示，可以表示为 ϕ = arccos ⁡ a z ∣ a ∣ \phi=\arccos\frac{a_z}{|\boldsymbol{a}|} ϕ=arccos∣a∣az。方位角表示向量在 x − y x-y x−y 平面上的投影与 x x x 轴之间的夹角，通常用 θ \theta θ 表示，可以表示为 θ = arctan ⁡ a y a x \theta=\arctan\frac{a_y}{a_x} θ=arctanaxay。二、矩阵的基本概念 A. 矩阵的定义

矩阵是一个由 m m m 行 n n n 列元素排列成的矩形阵列，可以表示为：

A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn

其中 a i j a_{ij} aij 表示矩阵 A \boldsymbol{A} A 中第 i i i 行第 j j j 列的元素。矩阵的大小为 m × n m\times n m×n，其中 m m m 表示矩阵的行数， n n n 表示矩阵的列数。

矩阵可以用于表示线性变换、解线性方程组、表示多项式等等。在机器学习和深度学习中，矩阵也是非常重要的数据结构之一，常用于表示样本数据和模型参数。

B. 矩阵的运算：加法、数乘和乘法

矩阵的运算包括加法、数乘和乘法，它们的定义如下：

矩阵加法：设有两个 m × n m\times n m×n 的矩阵 A \boldsymbol{A} A 和 B \boldsymbol{B} B，则它们的和 A + B \boldsymbol{A}+\boldsymbol{B} A+B 定义为一个 m × n m\times n m×n 的矩阵，其每个元素都等于相应位置上 A \boldsymbol{A} A 和 B \boldsymbol{B} B 中对应元素的和，即：

( A + B ) i j = a i j + b i j (\boldsymbol{A}+\boldsymbol{B})_{ij} = a_{ij}+b_{ij} (A+B)ij=aij+bij

矩阵数乘：设有一个标量 k k k 和一个 m × n m\times n m×n 的矩阵 A \boldsymbol{A} A，则它们的积 k A k\boldsymbol{A} kA 定义为一个 m × n m\times n m×n 的矩阵，其每个元素都等于相应位置上 A \boldsymbol{A} A 中对应元素乘以 k k k 的结果，即：

( k A ) i j = k a i j (k\boldsymbol{A})_{ij} = ka_{ij} (kA)ij=kaij

矩阵乘法：设有两个矩阵 A \boldsymbol{A} A 和 B \boldsymbol{B} B，如果 A \boldsymbol{A} A 的列数等于 B \boldsymbol{B} B 的行数，则它们的乘积 A B \boldsymbol{A}\boldsymbol{B} AB 定义为一个 m × p m\times p m×p 的矩阵，其中第 i i i 行第 j j j 列的元素为：

( A B ) i j = ∑ k = 1 n a i k b k j (\boldsymbol{A}\boldsymbol{B})_{ij} = \sum_{k=1}^na_{ik}b_{kj} (AB)ij=k=1∑naikbkj

其中 m m m 表示 A \boldsymbol{A} A 的行数， n n n 表示 A \boldsymbol{A} A 的列数， p p p 表示 B \boldsymbol{B} B 的列数。需要注意的是，矩阵乘法不满足交换律，即一般情况下 A B ≠ B A \boldsymbol{A}\boldsymbol{B}\neq\boldsymbol{B}\boldsymbol{A} AB=BA。

矩阵的加法和数乘都是逐个对应元素进行操作，因此也称为元素级别的操作。矩阵乘法可以看做是一种特殊的线性变换，它将一个矩阵映射为另一个矩阵，是线性代数中非常重要的运算。

C. 矩阵的转置和逆

矩阵的转置和逆是矩阵运算中比较重要的概念，它们的定义如下：

矩阵转置：设有一个 m × n m\times n m×n 的矩阵 A \boldsymbol{A} A，则它的转置 A T \boldsymbol{A}^T AT 是一个 n × m n\times m n×m 的矩阵，其每个元素满足：

( A T ) i j = a j i (\boldsymbol{A}^T)_{ij} = a_{ji} (AT)ij=aji

即将矩阵 A \boldsymbol{A} A 的行和列交换，得到的新矩阵就是 A \boldsymbol{A} A 的转置矩阵。

矩阵逆：设有一个 n × n n\times n n×n 的方阵 A \boldsymbol{A} A，如果存在一个 n × n n\times n n×n 的方阵 B \boldsymbol{B} B，满足：

A B = B A = I \boldsymbol{A}\boldsymbol{B} = \boldsymbol{B}\boldsymbol{A} = \boldsymbol{I} AB=BA=I

其中 I \boldsymbol{I} I 是 n × n n\times n n×n 的单位矩阵，则称矩阵 A \boldsymbol{A} A 可逆，并且称矩阵 B \boldsymbol{B} B 是 A \boldsymbol{A} A 的逆矩阵，记作 A − 1 \boldsymbol{A}^{-1} A−1。需要注意的是，只有方阵才有逆矩阵。

矩阵转置和逆矩阵是矩阵运算中非常重要的概念。矩阵转置可以将矩阵行和列的顺序交换，方便进行某些运算。矩阵逆是线性代数中一个非常重要的概念，它可以用来解线性方程组、求解最小二乘问题等等。如果一个矩阵不可逆，则称该矩阵是奇异的。

D. 矩阵的秩和行列式

矩阵的秩和行列式是矩阵运算中比较重要的概念，它们的定义如下：

矩阵秩：设有一个 m × n m\times n m×n 的矩阵 A \boldsymbol{A} A，如果矩阵 A \boldsymbol{A} A 的秩为 r r r，则称 A \boldsymbol{A} A 是一个秩为 r r r 的矩阵，记作 rank ⁡ ( A ) = r \operatorname{rank}(\boldsymbol{A})=r rank(A)=r。矩阵的秩表示矩阵中线性无关的行或列的最大数量。

矩阵行列式：设有一个 n × n n\times n n×n 的方阵 A \boldsymbol{A} A，则它的行列式 det ⁡ ( A ) \det(\boldsymbol{A}) det(A) 是一个标量值，其计算方式如下：

det ⁡ ( A ) = ∑ σ ∈ S n ( − 1 ) sgn ⁡ ( σ ) a 1 σ ( 1 ) a 2 σ ( 2 ) ⋯ a n σ ( n ) \det(\boldsymbol{A}) = \sum_{\sigma\in S_n} (-1)^{\operatorname{sgn}(\sigma)} a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)} det(A)=σ∈Sn∑(−1)sgn(σ)a1σ(1)a2σ(2)⋯anσ(n)

其中 S n S_n Sn 是 n n n 个元素的置换群， σ \sigma σ 是其中的一个置换， sgn ⁡ ( σ ) \operatorname{sgn}(\sigma) sgn(σ) 是置换 σ \sigma σ 的符号（即逆序数的奇偶性）， a i σ ( i ) a_{i\sigma(i)} aiσ(i) 表示矩阵 A \boldsymbol{A} A 中第 i i i 行 σ ( i ) \sigma(i) σ(i) 列的元素。

矩阵秩和行列式是矩阵运算中非常重要的概念。矩阵秩可以用于判断矩阵中行或列的线性无关性，从而帮助我们解决线性方程组的问题。矩阵行列式是一个重要的标量值，可以用于判断矩阵是否可逆，从而帮助我们解决一些与矩阵逆有关的问题。

三、向量空间与线性变换 A. 向量空间的定义和性质

向量空间是一种数学结构，它由一组向量和一些运算构成。向量空间的定义如下：

设 V V V 是一个非空集合， F F F 是一个数域，如果对于 V V V 中的任意两个元素 u \boldsymbol{u} u 和 v \boldsymbol{v} v，以及 F F F 中的任意一个元素 k k k，定义了 V V V 上的加法和数乘两种运算，使得对于任意 u \boldsymbol{u} u， v \boldsymbol{v} v 和 w \boldsymbol{w} w，以及任意 k k k 和 l l l，满足以下八条性质：

加法满足交换律，即 u + v = v + u \boldsymbol{u}+\boldsymbol{v}=\boldsymbol{v}+\boldsymbol{u} u+v=v+u；加法满足结合律，即 ( u + v ) + w = u + ( v + w ) (\boldsymbol{u}+\boldsymbol{v})+\boldsymbol{w}=\boldsymbol{u}+(\boldsymbol{v}+\boldsymbol{w}) (u+v)+w=u+(v+w)；存在一个元素 0 ∈ V \boldsymbol{0}\in V 0∈V，使得对于任意 u ∈ V \boldsymbol{u}\in V u∈V，有 u + 0 = u \boldsymbol{u}+\boldsymbol{0}=\boldsymbol{u} u+0=u；对于任意 u ∈ V \boldsymbol{u}\in V u∈V，存在元素 − u ∈ V -\boldsymbol{u}\in V −u∈V，使得 u + ( − u ) = 0 \boldsymbol{u}+(-\boldsymbol{u})=\boldsymbol{0} u+(−u)=0；数乘满足结合律，即 k ( l u ) = ( k l ) u k(l\boldsymbol{u})=(kl)\boldsymbol{u} k(lu)=(kl)u；数乘满足分配律，即 ( k + l ) u = k u + l u (k+l)\boldsymbol{u}=k\boldsymbol{u}+l\boldsymbol{u} (k+l)u=ku+lu；数乘满足分配律，即 k ( u + v ) = k u + k v k(\boldsymbol{u}+\boldsymbol{v})=k\boldsymbol{u}+k\boldsymbol{v} k(u+v)=ku+kv；对于任意 u ∈ V \boldsymbol{u}\in V u∈V，有 1 u = u 1\boldsymbol{u}=\boldsymbol{u} 1u=u。

则称 V V V 是一个向量空间， F F F 是向量空间 V V V 的数域。

向量空间具有以下基本性质：

向量空间中的元素称为向量；向量空间中的加法满足交换律、结合律和存在加法逆元；向量空间中的数乘满足分配律和结合律；向量空间中的数乘分配于加法，即 k ( u + v ) = k u + k v k(\boldsymbol{u}+\boldsymbol{v})=k\boldsymbol{u}+k\boldsymbol{v} k(u+v)=ku+kv 和 ( k + l ) u = k u + l u (k+l)\boldsymbol{u}=k\boldsymbol{u}+l\boldsymbol{u} (k+l)u=ku+lu；向量空间中有一个零向量，使得对于任何向量 u \boldsymbol{u} u，有 u + 0 = u \boldsymbol{u}+\boldsymbol{0}=\boldsymbol{u} u+0=u；向量空间中的加法和数乘都满足分配律，即 ( k + l ) u = k u + l u (k+l)\boldsymbol{u}=k\boldsymbol{u}+l\boldsymbol{u} (k+l)u=ku+lu 和 k ( u + v ) = k u + k v k(\boldsymbol{u}+\boldsymbol{v})=k\boldsymbol{u}+k\boldsymbol{v} k(u+v)=ku+kv；向量空间中的每个向量都有一个加法逆元素 − u -\boldsymbol{u} −u，使得 u + ( − u ) = 0 \boldsymbol{u}+(-\boldsymbol{u})=\boldsymbol{0} u+(−u)=0；向量空间中的数乘具有单位元，即 1 u = u 1\boldsymbol{u}=\boldsymbol{u} 1u=u；向量空间中的向量可以进行加法和数乘运算。

向量空间是许多数学领域中的重要概念，如线性代数、微积分、拓扑学等。

B. 线性变换的定义和性质

线性变换是一种将一个向量空间映射到另一个向量空间的映射，它满足以下两个条件：

对于任意向量 u , v \boldsymbol{u}, \boldsymbol{v} u,v 和标量 k k k，都有 T ( u + v ) = T ( u ) + T ( v ) T(\boldsymbol{u} + \boldsymbol{v}) = T(\boldsymbol{u}) + T(\boldsymbol{v}) T(u+v)=T(u)+T(v) 和 T ( k u ) = k T ( u ) T(k\boldsymbol{u}) = kT(\boldsymbol{u}) T(ku)=kT(u)。线性变换必须将零向量 0 \boldsymbol{0} 0 映射为零向量 0 \boldsymbol{0} 0。

线性变换的性质包括：

线性变换在向量加法和数乘下是保持的。线性变换将原空间的线性相关向量映射到目标空间的线性相关向量，将线性无关向量映射为线性无关向量。线性变换将原空间中的基向量映射为目标空间中的基向量。线性变换将原空间中的任何向量映射为目标空间中的一个向量。

线性变换在许多数学领域中都有广泛应用，如线性代数、微积分、信号处理等。

C. 线性变换的矩阵表示

线性变换可以通过矩阵进行表示。设 T T T 是一个将 n n n 维向量空间 V V V 映射到 m m m 维向量空间 W W W 的线性变换， { e 1 , e 2 , … , e n } \{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\} {e1,e2,…,en} 和 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 是 V V V 和 W W W 中的基向量，则 T T T 可以表示为一个 m × n m \times n m×n 的矩阵 A A A，其中 A A A 的第 j j j 列表示 T ( e j ) T(\boldsymbol{e}_j) T(ej) 在 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标。

具体地，设 v = x 1 e 1 + x 2 e 2 + ⋯ + x n e n \boldsymbol{v} = x_1\boldsymbol{e}_1 + x_2\boldsymbol{e}_2 + \cdots + x_n\boldsymbol{e}_n v=x1e1+x2e2+⋯+xnen 是 V V V 中的一个向量，则 T ( v ) T(\boldsymbol{v}) T(v) 在基 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标是矩阵向量乘积：

在这里插入图片描述

其中 y 1 , y 2 , … , y m y_1,y_2,\dots,y_m y1,y2,…,ym 分别是 T ( v ) T(\boldsymbol{v}) T(v) 在基 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标。

矩阵 A A A 的第 j j j 列就是 T ( e j ) T(\boldsymbol{e}_j) T(ej) 在基 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标，因此有：

A = [ ∣ ∣ ∣ T ( e 1 ) T ( e 2 ) ⋯ T ( e n ) ∣ ∣ ∣ ] f 1 f 2 ⋯ f m A = \begin{bmatrix} \vert & \vert & & \vert \\ T(\boldsymbol{e}_1) & T(\boldsymbol{e}_2) & \cdots & T(\boldsymbol{e}_n) \\ \vert & \vert & & \vert \end{bmatrix} \begin{matrix} \\ \boldsymbol{f}_1 \\ \\ \end{matrix} \begin{matrix} \\ \boldsymbol{f}_2 \\ \\ \end{matrix} \cdots \begin{matrix} \\ \boldsymbol{f}_m \\ \\ \end{matrix} A= ∣T(e1)∣∣T(e2)∣⋯∣T(en)∣ f1f2⋯fm

注意到矩阵 A A A 的第 j j j 列可以看作是将 e j \boldsymbol{e}_j ej 映射为 f 1 , f 2 , … , f m \boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m f1,f2,…,fm 中各个向量的系数，因此矩阵乘法 A x A\boldsymbol{x} Ax 可以看作是将向量 x \boldsymbol{x} x 在基 { e 1 , e 2 , … , e n } \{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\} {e1,e2,…,en} 下的坐标，通过线性变换 T T T 转换为基 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标。

因此，对于任意向量 v \boldsymbol{v} v，都有：

[ T ( v ) ] { f 1 , f 2 , … , f m } = A [ v ] { e 1 , e 2 , … , e n } [T(\boldsymbol{v})]_{\{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\}} = A [\boldsymbol{v}]_{\{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\}} [T(v)]{f1,f2,…,fm}=A[v]{e1,e2,…,en}

其中 [ v ] { e 1 , e 2 , … , e n } [\boldsymbol{v}]_{\{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\}} [v]{e1,e2,…,en} 和 [ T ( v ) ] { f 1 , f 2 , … , f m } [T(\boldsymbol{v})]_{\{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\}} [T(v)]{f1,f2,…,fm} 分别是向量 v \boldsymbol{v} v 在基 { e 1 , e 2 , … , e n } \{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\} {e1,e2,…,en} 和 T ( v ) T(\boldsymbol{v}) T(v) 在基 { f 1 , f 2 , … , f m } \{\boldsymbol{f}_1,\boldsymbol{f}_2,\dots,\boldsymbol{f}_m\} {f1,f2,…,fm} 下的坐标。

因此，矩阵 A A A 也被称为线性变换 T T T 的标准矩阵，表示在基 { e 1 , e 2 , … , e n } \{\boldsymbol{e}_1,\boldsymbol{e}_2,\dots,\boldsymbol{e}_n\} {e1,e2,…,en} 下， T T T 的向量表示的系数矩阵。

D. 线性变换的特征值和特征向量

对于线性变换 T T T，如果存在标量 λ \lambda λ 和非零向量 v \boldsymbol{v} v，满足：

T ( v ) = λ v T(\boldsymbol{v}) = \lambda \boldsymbol{v} T(v)=λv

则称 λ \lambda λ 是线性变换 T T T 的特征值， v \boldsymbol{v} v 是线性变换 T T T 的对应于特征值 λ \lambda λ 的特征向量。

可以证明，对于特征向量 v \boldsymbol{v} v，如果 T ( v ) = λ v T(\boldsymbol{v}) = \lambda \boldsymbol{v} T(v)=λv，那么对于任意实数 k k k，都有 T ( k v ) = λ ( k v ) T(k\boldsymbol{v}) = \lambda (k\boldsymbol{v}) T(kv)=λ(kv)，也就是说， k v k\boldsymbol{v} kv 仍然是 T T T 的特征向量，对应的特征值仍然是 λ \lambda λ。因此，特征向量是由一个特征向量生成的一维向量空间上的所有向量。

特征值和特征向量可以用于矩阵的对角化，即将矩阵表示为对角矩阵的形式，使得矩阵的主对角线上是特征值。具体来说，设 A A A 是一个 n × n n\times n n×n 的矩阵，如果存在一个可逆矩阵 P P P，使得 P − 1 A P P^{-1}AP P−1AP 是一个对角矩阵，那么 P − 1 A P P^{-1}AP P−1AP 的主对角线上的元素就是 A A A 的特征值，对应的 P P P 的列向量就是 A A A 的特征向量。

对角化的一个重要应用是矩阵的幂运算，如果矩阵 A A A 可对角化为 P − 1 A P = d i a g ( λ 1 , λ 2 , … , λ n ) P^{-1}AP=\mathrm{diag}(\lambda_1,\lambda_2,\dots,\lambda_n) P−1AP=diag(λ1,λ2,…,λn)，那么矩阵 A A A 的幂可以写成：

A k = ( P − 1 A P ) k = P − 1 A k P = P − 1 d i a g ( λ 1 k , λ 2 k , … , λ n k ) P A^k = (P^{-1}AP)^k = P^{-1}A^kP = P^{-1}\mathrm{diag}(\lambda_1^k,\lambda_2^k,\dots,\lambda_n^k)P Ak=(P−1AP)k=P−1AkP=P−1diag(λ1k,λ2k,…,λnk)P

这个式子可以更方便地计算矩阵的幂，特别是在计算大矩阵幂时。

四、向量和矩阵在机器学习中的应用 A. 数据的表示：向量和矩阵

向量和矩阵是机器学习中最基础的数据表示方式之一，几乎所有的机器学习算法都是以向量和矩阵为输入和输出的。在机器学习中，数据通常是以向量的形式表示，每个样本用一个特征向量表示，而特征向量中的每个分量则代表一个特征，比如图像数据可以表示成像素强度的向量，文本数据可以表示成词频向量等。在这些向量构成的向量空间中，机器学习算法通过对向量空间的数学操作来对数据进行处理和学习。

而矩阵则更多地用于描述多个样本的特征，比如在神经网络中，多个样本的输入数据可以用一个矩阵表示，其中每行代表一个样本的特征向量。矩阵在机器学习中的应用非常广泛，比如在深度学习中，神经网络的每一层都可以表示为一个矩阵，每个神经元可以看成是一个特定的权重矩阵。此外，矩阵还可以表示协方差矩阵、转移矩阵等。

在机器学习中，向量和矩阵的运算也非常重要。比如，向量的点积、向量的模长、矩阵的转置、矩阵的逆等都是机器学习中经常用到的操作。此外，矩阵的特征值和特征向量也广泛用于机器学习中的降维、聚类等算法中。

总之，向量和矩阵是机器学习中最基础的数据表示方式，它们不仅能够方便地表示数据，而且可以通过向量和矩阵的运算来实现对数据的处理和学习。

B. 线性回归和矩阵求解

在机器学习中，线性回归是一种常用的算法，而向量和矩阵的运算则是线性回归的关键。在线性回归中，我们通常使用向量和矩阵来表示样本和模型参数，并使用矩阵求解来计算模型参数的最优解。

具体来说，在线性回归中，我们用一个向量 x x x表示一个样本的特征，用向量 y y y表示该样本的标签。模型的参数用向量 θ \theta θ表示，模型可以表示为 h θ ( x ) = θ T x h_{\theta}(x)=\theta^Tx hθ(x)=θTx。线性回归的目标是找到一组最优的模型参数 θ \theta θ，使得模型 h θ ( x ) h_{\theta}(x) hθ(x)与真实标签 y y y的误差最小化。

将所有的样本数据表示为矩阵 X X X和标签向量 y y y，则线性回归的最优解可以通过矩阵求解的方式求得。具体来说，我们可以通过最小二乘法来求解最优解，即：

θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy

其中， ( X T X ) − 1 (X^TX)^{-1} (XTX)−1为矩阵 X T X X^TX XTX的逆矩阵， X T X^T XT为矩阵 X X X的转置矩阵。

除了线性回归外，矩阵求解还可以应用于其他机器学习算法中。比如，在深度学习中，反向传播算法中的梯度计算和权重更新都可以通过矩阵求解来实现。此外，在机器学习中，矩阵求解还可以用于矩阵分解、最优化问题等。

因此，向量和矩阵在机器学习中的应用非常广泛，它们不仅能够方便地表示数据和模型参数，而且可以通过矩阵求解等数学方法来实现对数据的处理和学习。

C. 主成分分析（PCA）和特征向量

主成分分析（PCA）是一种常用的降维算法，它的核心就是使用特征向量和矩阵运算来实现数据的降维。具体来说，PCA可以通过以下几个步骤来实现：

去中心化：对数据进行中心化处理，即对每个特征减去该特征的均值。计算协方差矩阵：对去中心化后的数据计算协方差矩阵，该矩阵反映了不同特征之间的关系。特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量。选择主成分：根据特征值的大小，选择前k个特征向量作为新的基向量，将原始数据投影到这个新的子空间中，实现降维。

在PCA算法中，特征向量和特征值起着非常重要的作用。特征向量是一个向量，它在矩阵变换后只发生长度的变化而不发生方向的变化；而特征值则是对应于特征向量的标量，表示矩阵变换在该方向上的伸缩程度。

在PCA算法中，特征向量表示了数据在新的子空间中的基向量，而特征值则表示了每个新的基向量对应的方差大小，即新的子空间中每个维度的重要性大小。通过选择最大的k个特征值对应的特征向量，我们就可以得到一个新的k维子空间，将原始数据投影到这个新的子空间中，从而实现数据的降维。

总的来说，向量和矩阵在机器学习中的应用非常广泛，不仅可以方便地表示数据和模型参数，还可以通过矩阵运算和特征分解等数学方法来实现数据的降维、特征提取、模型优化等任务。

D. 矩阵分解和推荐系统

在机器学习中，矩阵分解是一个非常重要的技术。它可以用于许多任务，包括推荐系统、文本分析、图像处理等。

推荐系统通常使用矩阵分解来预测用户可能喜欢的产品或服务。这可以通过将用户-产品矩阵分解为用户特征和产品特征矩阵来实现。通过这种方式，推荐系统可以预测未被用户评价的产品或服务的评分，并向用户推荐他们可能感兴趣的产品或服务。

另一个使用矩阵分解的示例是文本分析。文本可以表示为单词-文档矩阵，其中每行代表一个单词，每列代表一个文档。这个矩阵可以分解为单词特征和文档特征矩阵。通过这种方式，可以对文档进行分类、聚类或提取主题等。

图像处理也使用了矩阵分解。图像可以表示为像素矩阵，可以通过将像素矩阵分解为基础特征和权重矩阵来实现。这可以用于图像压缩、去噪或增强等。

总之，矩阵分解是一种非常强大的工具，可以应用于许多机器学习任务中，例如推荐系统、文本分析和图像处理等。

【本文地址】

线性代数基础

线性代数基础

今日新闻

推荐新闻