矩阵笔记1:矩阵分析(第三版) |
您所在的位置:网站首页 › 矩阵分析引论第四版答案解析视频讲解 › 矩阵笔记1:矩阵分析(第三版) |
矩阵笔记1:矩阵分析(第三版)
|
文章目录
0 笔记说明1 书本内容1.1 线性空间1.2 基与坐标、坐标变换1.3 线性子空间1.4 线性映射1.5 线性映射的值域、核1.6 线性变换的矩阵与线性变换的运算1.7 n维线性空间的同构1.8 线性变换的特征值与特征向量1.9 线性变换的不变子空间1.10 矩阵的相似对角形
2 听课笔记2.1 线性空间2.2 基与坐标、坐标变换2.3 线性子空间2.4 线性映射2.5 线性映射的值域、核2.6 线性变换的矩阵与线性变换的运算2.7 n维线性空间的同构2.8 线性变换的特征值与特征向量2.9 线性变换的不变子空间2.10 矩阵的相似对角形
0 笔记说明
参考书籍为: 本篇博客是关于第一章的内容,下面开始即为正文。 1 书本内容本篇博客将简要地介绍线性空间,所考虑的数域是实数域(记为R)和复数域(记为C),统称数域F。 1.1 线性空间1、线性空间:设V是一个非空集合,F是一个数域,在集合V的元素之间定义了加法运算,即对于V中任意两个元素α与β,在V中都有唯一的元素v与它们相对应,称之为α与β的和,记为v=α+β,并且加法运算满足下面四条法则: (1)交换律:α+β=β+α; (2)结合律:α+(β+γ)=(α+β)+γ; (3)零元素:在V中有一元素0(称作零元素),对于V中任一元素α都有α+0=α; (4)负元素:对于V中每一个元素α,都有V中的元素β,使得α+β=0。 上面四条法则中,α、β、γ为V中的任意三个元素,α、β、γ∈V。除此之外,在集合V中的元素与数域F中的数之间还定义了一种运算,叫做数乘,即对于V中任一元素α与F中任一数k,在V中有唯一的一个元素η与它们对应,称为k与α的数乘,记为η=k·α=kα,并且数乘运算满足下面四条法则: (1)1·α=α; (2)(kl)α=k(lα); (3)(k+l)α=kα+lα; (4)k(α+β)=kα+kβ。 上面四条法则中,k,l为F中的任意两个数,k、l∈F。则称集合V为数域F上的线性空间。 2、矩阵的核空间/零空间:设A为实数域(或复数域)上的m×n阶矩阵,易证:齐次线性方程组Ax=0的所有解(包括零解)的集合构成实数域(或复数域)上的线性空间。此空间为方程组Ax=0的解空间,也称为矩阵A的核空间或零空间,用N(A)表示。 3、矩阵的值域/列空间:设A为实数域(或复数域)上的m×n阶矩阵,x为n维列向量,则m维列向量集合V={y∈Rm(或Cm) I y=Ax,x∈Rn(或Cn),A∈Rm×n(Cm×n)}构成实数域(或复数域)上的线性空间,称为A的列空间或A的值域,用R(A)表示。 4、线性表示/线性组合:设V是数域F上的线性空间,α1,α2,…,αr是V中的任意一组向量(其中r≥1),k1,k2,…,kr是数域F中的一组数。若向量α可以表示成α=k1α1+k2α2+…+krαr,则称α可由α1,α2,…,αr线性表示或线性表出,同时也可以称α是α1,α2,…,αr的线性组合。 5、线性相关/线性无关:设α1,α2,…,αr是线性空间V中的一组向量(其中r≥1)。如果在数域F中有r个不全为零的数k1,k2,…,kr,使得k1α1+k2α2+…+krαr=0,则称α1,α2,…,αr线性相关。如果一组向量α1,α2,…,αr不线性相关,就称为线性无关。换言之,若k1α1+k2α2+…+krαr=0当且仅当k1=k2=…kr=0,便称α1,α2,…,αr线性无关。一组向量要么线性相关,要么线性无关,非此即彼。 6、线性表出唯一定理:设线性空间V中向量组α1,α2,…,αm线性无关,且向量组α1,α2,…,αm,β线性相关,则β可由α1,α2,…,αm线性表出,且表出是唯一的。 1.2 基与坐标、坐标变换1、基、坐标、维数:设数域F上的线性空间V中有n个线性无关向量α1,α2,…,αn,而且V中任何一个向量α都可由α1,α2,…,αn线性表出:α=k1α1+k2α2+…+knαn,则称α1,α2,…,αn为V的一个基,(k1,k2,…,kn)T为α在基α1,α2,…,αn下的坐标,称V为n维线性空间,并记dimV=n。 2、过渡矩阵:设α1,α2,…,αn与β1,β2,…,βn是V中的任意两个基,它们之间的关系是: 3、坐标变换:设ξ∈V,若ξ在基α1,α2,…,αn与β1,β2,…,βn下的坐标分别为(x1,x2,…,xn)T与(y1,y2,…,yn)T,即若有: 4、使用可逆矩阵将旧的一个基变成新的一个基:设α1,α2,…,αn为线性空间V的一个基,A为可逆矩阵,记(α1,α2,…,αn)P为β1,β2,…,βn,即(β1,β2,…,βn)=(α1,α2,…,αn)P,则β1,β2,…,βn也为V的一个基。 1.3 线性子空间1、线性子空间:设W是数域F上的线性空间V的一个非空子集,若W关于V的加法和数乘运算也构成线性空间,则称W是V的一个线性子空间,简称为子空间,dim W ≤ dim V。 2、平凡子空间:在线性空间V中,由单个零向量“0”构成的集合是一个线性子空间,称为V的零子空间。在线性空间V中,V本身也可看成是一个线性子空间。这两个子空间称为V的平凡子空间,其他子空间称为为非平凡子空间。 3、生成子空间:设α1,α2,…,αs是线性空间V中一组向量,则集合span{α1,α2,…,αs}={k1α1+k2α2+…+ksαs|∀ki∈F}是非空集合,则span{α1,α2,…,αs}是V的线性子空间。称非空子集span{α1,α2,…,αs}是由向量α1,α2,…,αs生成的生成子空间。 4、生成子空间的维数:dim span{α1,α2,…,αs}=rank{α1,α2,…,αs},其中rank{α1,α2,…,αs}是向量组α1,α2,…,αs的秩。向量组α1,α2,…,αs的任何一个极大线性无关组均可作为span{α1,α2,…,αs}的一个基。 5、生成子空间之间的等价:若α1,α2,…,αs与β1,β2,…,βt都是n维向量组,则span{α1,α2,…,αs}=span{β1,β2,…,βt}⇔α1,α2,…,αs与β1,β2,…,βt等价,即α1,α2,…,αs与β1,β2,…,βt可以互相线性表示。 6、交空间与和空间:设V1,V2是线性空间V的两个子空间,命V1∩V2={αlα∈V1且α∈V2},则V1∩V2构成V的线性子空间。称V1∩V2为V1与V2的交空间。命V1+V2={α=α1+α2lα1∈V1且α2∈V2},则V1+V2构成V的线性子空间。称V1+V2为V1与V2的和空间。 7、生成子空间的和:设V1=span{α1,α2,…,αs},V2=span{β1,β2,…,βt},则V1+V2=span{α1,α2,…,αs,β1,β2,…,βt}。 8、维数公式:设V1与V2是线性空间V的两个子空间,则dimV1+dimV2=dim(V1+V2)+dim(V1∩V2)。 9、直和:如果W1+W2中的任何一个向量均可以唯一分解成W1和W2中的两个向量之和,则称W1+W2为直和,记为W1⊕W2。 10、直和的判定:设W1,W2是线性空间V的两个子空间,则下列命题等价:① W1+W2是直和;② 0的分解唯一;③ W1∩W2={0};④ dim(W1+W2)=dim(W1)+dim(W2);⑤ W1,W2的基一起构成W1+W2的基。 11、直和分解与代数补:设W,W1,W2是线性空间V的三个子空间,且W=W1⊕W2,则称W有一个直和分解。特别地,若W=V=W1⊕W2,便称W1和W2是线性空间V的一对互补的子空间,或称W1是W2的代数补子空间,也可称W2是W1的代数补子空间。 12、代数补子空间存在定理:设U是线性空间V的一个子空间,则一定存在U的代数补子空间W,使得V=U⊕W。 1.4 线性映射1、线性映射:设V1,V2是数域F上的两个线性空间,映射𝒜:V1→V2,如果对于任何两个向量α1,α2∈V1和任何数λ∈F,都有𝒜(α1+α2)=𝒜(α1)+𝒜(α2);𝒜(λα1)=λ𝒜(α1),便称映射𝒜是由定义域V1到像集α2的线性映射。称α1为𝒜(α1)的原像,𝒜(α1)为α1的像。 2、线性映射的性质:① 𝒜(0)=0;② ∀αi∈V,∀ki∈F,有𝒜(Σi∈[1,s]kiαi)=Σi∈[1,s]ki𝒜(αi);③ 设α1,α2,…,αs∈V1,α1,α2,…,αs线性相关,则𝒜(α1),𝒜(α2),…,𝒜(αs)也线性相关。特别要注意,若α1,α2,…,αs∈V1,且线性无关,则𝒜(α1),𝒜(α2),…,𝒜(αs)不一定线性无关。 3、线性映射对应的矩阵:设α1,α2,…,αn是V1的一个基,β1,β2,…,βm是V2的一个基,𝒜是V1→V2的一个线性映射,则: 4、原像与像的坐标关系:设α1,α2,…,αn是V1的一个基,∀α∈V1,故: 5、矩阵对应的线性映射:设V1的基为α1,α2,…,αn,V2的基为β1,β2,…,βm,给定m×n矩阵A=(aij)m×n,则存在唯一的线性映射𝒜,𝒜在这两个基下的矩阵表示为A。 6、线性映射在不同对基下的矩阵是等价的:设𝒜是V1→V2的一个线性映射,α’1,α’2,…,α’n与α1,α2,…,αn是V1的两个基,由αi到α’i的过渡矩阵为P。设β’1,β’2,…,β’m与β1,β2,…,βm是V2的两个基,由βj到β’j的过渡矩阵为Q。线性映射𝒜在基α1,α2,…,αn与β1,β2,…,βm下的矩阵表示为A,在基α’1,α’2,…,α’n与β’1,β’2,…,β’m下的矩阵表示为B,则B=Q-1·A·P。 7、矩阵等价:设A,B∈Fm×n,若存在Q∈Fm×m,P∈Fn×n,满足B =Q·A·P,则称B与A等价。 8、矩阵与线性映射的关系:任何一个线性映射𝒜:Vn→Vm都有一系列的m×n矩阵表示:A,B,….。这些矩阵之间是互相等价的。互相等价的m×n矩阵代表同一个线性映射。原像α的坐标x=(x1,x2,…,xn)T与像𝒜(α)的坐标y=(y1,y2,…,ym)T之间满足式:y=Ax,这也揭示了m×n矩阵A是Cm→Cn的一个线性映射,它与线性映射𝒜:Vn→Vm是对应的。因此,一般的线性空间Vn与特殊的向量空间Fm同构(后面的1.7节会讨论同构),线性映射𝒜可用矩阵A代表。 1.5 线性映射的值域、核1、线性映射的值域:设𝒜是线性空间V1到V2的线性映射,命𝒜(V1)={𝒜(α)|∀α∈V1},𝒜(V1)是V2的线性子空间。称𝒜(V1)是线性映射𝒜的值域,记之为R(𝒜),称dim R(𝒜)为𝒜的秩,记之为rank𝒜。 2、线性映射的值域的表示:设𝒜是线性空间V1到V2的线性映射,α1,α2,…,αn是V1的基,β1,β2,…,βm是V2的基。在该对基下的矩阵表示为A=(aij)m×n,则:① R(𝒜)=span{𝒜(α1),𝒜(α2),…,𝒜(αn};② rank 𝒜=rank A。 3、线性映射的核:设𝒜是线性空间V1到V2的线性映射,命𝒜-1(0)={α|𝒜(α)=0,α∈V1}。𝒜-1(0)是V1的线性子空间,称𝒜-1(0)是线性映射𝒜的核子空间,记之为N(𝒜),称dim N(𝒜)为𝒜的零度。若dim N(𝒜)=0,则线性无关向量组α1,α2,…,αr∈V1的像𝒜(α1),𝒜(α2),…,𝒜(αr)∈V2也线性无关。 4、线性映射的零度与秩之和为V1的维数:𝒜是n维线性空间V1到m维线性空间V2的线性映射,则dim N(𝒜)+dim R(𝒜)=n。 5、矩阵的核空间与列空间的秩之和为矩阵的列数:若m×n矩阵A的秩为r,则对于齐次线性方程组Ax=0的解空间/核空间N(A),有dim N(A)=n-r,A的列空间R(A)满足dim R(A)=r,于是dim N(A)+dim R(A)=n。 6、线性映射的值域与矩阵的值域:设𝒜是n维线性空间V1到m维线性空间V2的线性映射,α1,α2,…,αn是V1的一个基,β1,β2,…,βm是V2的一个基。线性映射𝒜在这对基下的矩阵表示是m×n矩阵A=(A1,A2,…,An),其中Ai=(a1i,a2i,…,ami)T是m维列向量,i=1,2,…,n。于是:𝒜(α1,α2,…,αn)=(β1,β2,…,βm)A,因此𝒜(αi)=(β1,β2,…,βm)Ai,i=1,2,…,n。𝒜的值域R(𝒜)=span{𝒜(α1),𝒜(α2),…,𝒜(αn)}=span{(β1,β2,…,βm)A1,(β1,β2,…,βm)A2,…,(β1,β2,…,βm)An},而矩阵A的值域R(A)={y|Ax=y,x∈Rn},若取xi=(0,…,0,1,0,…,0)T,则Axi=Ai,i=1,2,…,n,所以R(A)=span{A1,A2,…,An}。综上所述:R(𝒜)与R(A)的表达式相同,即线性映射𝒜的值域与矩阵A的值域是一致的,只要把A的值域引进基,这样就与𝒜的值域完全相同。 7、线性映射的核与矩阵的核:设𝒜是n维线性空间V1到m维线性空间V2的线性映射,α1,α2,…,αn是V1的一个基,β1,β2,…,βm是V2的一个基。线性映射𝒜在这对基下的矩阵表示是m×n矩阵A,设X∈V1,则X可表示为: 1、线性变换中原像α与像𝒜(α)的坐标变换:若线性映射𝒜是指线性空间V到线性空间V的映射,称这样的𝒜为线性空间V的线性变换。由于线性变换是线性空间V到自身的映射,所以只需取V的一个基α1,α2,…,αn即可。设𝒜是线性空间V的线性变换,α1,α2,…,αn是V的一个基,若: 2、线性变换在不同对基下的矩阵是相似的:设𝒜是V到V的线性变换,α1,α2,…,αn与α’1,α’2,…,α’n是V的两个基。由α1,α2,…,αn到α’1,α’2,…,α’n的过渡矩阵为P,线性变换𝒜在基α1,α2,…,αn下的矩阵表示为A,在基α’1,α’2,…,α’n下的矩阵表示为B,则:B=P-1AP。 3、矩阵相似:设A,B∈Fn×n,若存在P∈Fn×n,满足B=P-1AP,则称B与A相似,记之为B~A。相似有三个性质:① 自反性:A~A;② 对称性:若B~A,则A~B;③ 传递性:若A~B,B~C,则A~C。 4、线性变换的运算:设𝒜,ℬ是线性空间V的两个线性变换,定义它们的乘积𝒜ℬ为𝒜ℬ(α)=𝒜(ℬ(α)),α∈V。定义线性变换的加法(𝒜+ℬ)为(𝒜+ℬ)(α)=𝒜(α)+ℬ(α)。定义数量乘法k𝒜为(k𝒜)(α)=k𝒜(α)。V的线性变换𝒜称为可逆的,如果有V的线性变换ℬ存在,满足𝒜ℬ=ℬ𝒜=E,其中E是恒等变换,这时变换ℬ称为𝒜的逆变换,记为𝒜-1。不难验证,上述定义的𝒜+ℬ,𝒜ℬ,k𝒜与𝒜-1都是线性变换。 5、线性变换的运算对应于矩阵的运算:在n维线性空间中取定一个基后,其上的一个线性变换𝒜就与一个n阶矩阵一一对应,而且这个对应保持在线性变换的运算上。设α1,α2,…,αn是n维线性空间V的一个基,在这个基下,线性变换𝒜对应于一个n阶矩阵A,线性变换ℬ对应于一个n阶矩阵B。这个对应具有以下的几个性质: (1)线性变换𝒜与ℬ的和𝒜+ℬ对应于矩阵A与B的和A+B; (2)线性变换𝒜的数量乘积k𝒜对应于矩阵A的数量乘积kA; (3)线性变换𝒜与ℬ的积𝒜ℬ对应于矩阵A与B的积AB; (4)若线性变换𝒜可逆,即𝒜-1存在,则𝒜对应的矩阵A可逆,且𝒜的逆变换𝒜-1对应于矩阵A的逆矩阵A-1。 1.7 n维线性空间的同构1、同构映射:V1与V2是两个不同的线性空间,若存在V1到V2上的一个一一对应δ,使得对于所有向量α,β∈V1,数λ∈F都有: (1)δ(α+β)=δ(α)+δ(β); (2)δ(λα)=λδ(α)。 则此一一对应δ称为V1到V2的同构映射,称V1与V2是同构的。举个栗子:n维线性空间V取定一组基α1,α2,…,αn后,则V中的向量与它的坐标(x1,x2,…,xn)T之间的一一对应是从V到Fn上的一个同构映射,且数域F上任一个n维线性空间都与n维列向量空间Fn同构。 2、同构映射的基本性质: (1)δ(0)=0,δ(-α)=-δ(α); (2)δ(k1α1+k2α2+…+ksαs)=k1δ(α1)+k2δ(α2)+…+ksδ(αs); (3)V中向量组α1,α2,…,αs线性相(无)关⇔像δ(α1),δ(α2),…,δ(αs)线性相(无)关; (4)如果V1是V的一个子空间,则V1在δ下的像集合δ(V1)={δ(α)|α∈V1}是δ(V)的子空间,并且V1与δ(V1)维数相同。 3、两个线性空间同构则维数相同:数域F上两个有限维线性空间同构⇔这两个线性空间有相同的维数。维数是有限维线性空间唯一的本质特征。举个栗子:根据同构映射的定义,R2×2中矩阵: 1、线性变换的特征值与特征向量:设𝒜是数域F上的n维线性空间V的线性变换,如果在V中存在一个非零向量α使得𝒜(α)=λ0α,其中λ0∈F,则称λ0是𝒜的一个特征值,称α是𝒜的属于特征值λ0的一个特征向量。从几何上看,变换前后的特征向量仍然共线,或者方向不变(λ0>0),或者方向相反(λ0 |
【本文地址】
今日新闻 |
推荐新闻 |
 本笔记主要是为了方便自己日后复习。由于未学习LaTeX,我会上传教材图片或者手写图片代替部分公式或内容。博客主要分为两部分:【1 书本内容】与【2 听课笔记】,前者为对教材中重要定理、定义的整理,后者为自己在矩阵上课时的笔记的二次书面整理。根据自身学习需要,我可能会增加必要内容。
本笔记主要是为了方便自己日后复习。由于未学习LaTeX,我会上传教材图片或者手写图片代替部分公式或内容。博客主要分为两部分:【1 书本内容】与【2 听课笔记】,前者为对教材中重要定理、定义的整理,后者为自己在矩阵上课时的笔记的二次书面整理。根据自身学习需要,我可能会增加必要内容。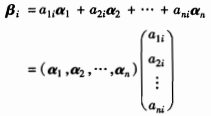 上图中i=1,2,…,n。将这n个关系式用矩阵记号可以表示成:
上图中i=1,2,…,n。将这n个关系式用矩阵记号可以表示成: 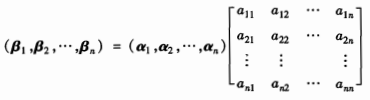 记n阶方阵为P:
记n阶方阵为P: 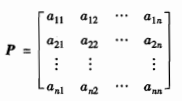 称矩阵P是由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵。矩阵P一定是可逆的,所以由基β1,β2,…,βn到基α1,α2,…,αn的过渡矩阵为P-1。可写成(β1,β2,…,βn)=(α1,α2,…,αn)P或者(α1,α2,…,αn)=(β1,β2,…,βn)P-1。
称矩阵P是由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵。矩阵P一定是可逆的,所以由基β1,β2,…,βn到基α1,α2,…,αn的过渡矩阵为P-1。可写成(β1,β2,…,βn)=(α1,α2,…,αn)P或者(α1,α2,…,αn)=(β1,β2,…,βn)P-1。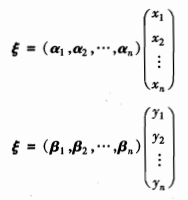 则有:
则有: 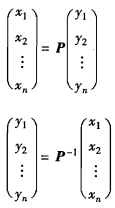 其中,矩阵P是由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵。称上图的两个公式为坐标变换公式。
其中,矩阵P是由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵。称上图的两个公式为坐标变换公式。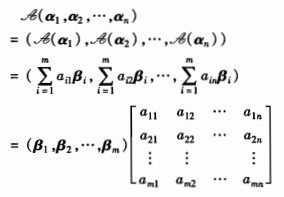 记矩阵A为:
记矩阵A为: 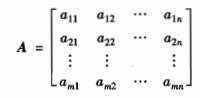 则:𝒜(α1,α2,…,αn)=(β1,β2,…,βm)A,矩阵A称为线性映射𝒜在基(α1,α2,…,αn)与基(β1,β2,…,βm)下的矩阵表示。
则:𝒜(α1,α2,…,αn)=(β1,β2,…,βm)A,矩阵A称为线性映射𝒜在基(α1,α2,…,αn)与基(β1,β2,…,βm)下的矩阵表示。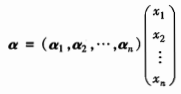 α的像𝒜(α)∈V2,设β1,β2,…,βm是V2的一个基,则𝒜(α)可写为:
α的像𝒜(α)∈V2,设β1,β2,…,βm是V2的一个基,则𝒜(α)可写为: 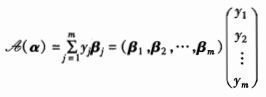 又因为:
又因为: 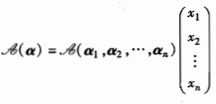 而上式等于:
而上式等于: 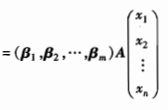 而矩阵A为:
而矩阵A为: 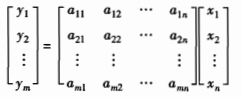 记上式为y=Ax,其中y=(y1,y2,…,ym)T,x=(x1,x2,…,xn)T,【y=Ax】称为线性映射𝒜在给定基(α1,α2,…,αn)与(β1,β2,…,βm)下向量坐标变换公式,即原像与像的坐标关系。
记上式为y=Ax,其中y=(y1,y2,…,ym)T,x=(x1,x2,…,xn)T,【y=Ax】称为线性映射𝒜在给定基(α1,α2,…,αn)与(β1,β2,…,βm)下向量坐标变换公式,即原像与像的坐标关系。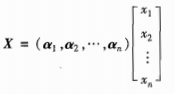 列向量(x1,x2,…,xn)T是V1中向量X在基α1,α2,…,αn下的坐标。N(𝒜)中的向量X一定满足:
列向量(x1,x2,…,xn)T是V1中向量X在基α1,α2,…,αn下的坐标。N(𝒜)中的向量X一定满足: 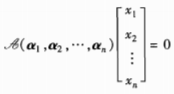 则有:
则有: 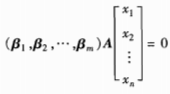 根据β1,β2,…,βm线性无关,得:
根据β1,β2,…,βm线性无关,得:  上式就是矩阵A的核(x1,x2,…,xn)T所满足的方程式。由此可见,𝒜的核N(𝒜)中的向量X在基α1,α2,…,αn下的坐标(x1,x2,…,xn)T满足矩阵A的核空间中的向量所满足的方程。因此线性映射𝒜的核与矩阵A的核是一致的,只要把矩阵A的核引进“基”以后就与线性映射𝒜的核完全相同。
上式就是矩阵A的核(x1,x2,…,xn)T所满足的方程式。由此可见,𝒜的核N(𝒜)中的向量X在基α1,α2,…,αn下的坐标(x1,x2,…,xn)T满足矩阵A的核空间中的向量所满足的方程。因此线性映射𝒜的核与矩阵A的核是一致的,只要把矩阵A的核引进“基”以后就与线性映射𝒜的核完全相同。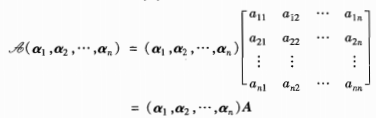 所以𝒜在α1,α2,…,αn下的矩阵表示——A是n阶方阵。设:
所以𝒜在α1,α2,…,αn下的矩阵表示——A是n阶方阵。设: 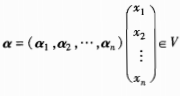 若:
若: 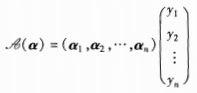 则原像α与像𝒜(α)的坐标变换公式为:
则原像α与像𝒜(α)的坐标变换公式为: 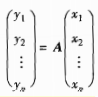
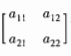 可以看做R4中的向量(α11,α12,α21,α22)T。
可以看做R4中的向量(α11,α12,α21,α22)T。