几种常用信号平滑去噪的方法(附Matlab代码) |
您所在的位置:网站首页 › 滤波去噪的概念和原理 › 几种常用信号平滑去噪的方法(附Matlab代码) |
几种常用信号平滑去噪的方法(附Matlab代码)
|
几种常用信号平滑去噪的方法(附Matlab代码)
1 滑动平均法
1.0 移动平均法的方法原理
1.1 matlab内自带函数实现移动平均法
1.2 利用卷积函数conv()实现移动平均法
1.3 利用filter滤波函数实现移动平均法
1.4 移动平均的幅频响应
1.5 时域和频域的转换关系
2 Savitzky-Golay法
2.1 Savitzky-Golay法的方法原理
2.2 Savitzky-Golay法的matlab实现
2.3 Savitzky-Golay法的幅频响应
3 处理离群值(粗大误差)的方法
3.1 中位值法
3.2 标准差法和MAD法
3.3 Matlab中其它离群值消除方法
4 其它一些FIR滤波器实现光滑去噪
4.1 FIR和IIR的区别
4.2 利用Matlab构建FIR滤波器
5 IIR滤波器实现光滑去噪
6 小波去噪方法
2020年8月更新:增加一个时域和频域的转换关系图,增加相应小节1.5 2021年8月更新:增加第6章小波去噪的内容 信号在实际测量中,难免会混入各种噪声。通常我们希望去除高频的随机噪声,或者是偏离正常测量太大的离群误差,以获得低频的测量数据。下面介绍几种常用的信号平滑去噪的方法。 还是惯例声明:本人没有相关的工程应用经验,只是纯粹对相关算法感兴趣才写此博客。所以如果有错误,欢迎在评论区指正,不胜感激。本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。 1 滑动平均法本章参考目录 1《数字信号处理》-胡广书 2《Digital Signal Processing - A Practical Guide For Engineers and Scientists》 - Steven W.Smith 1.0 移动平均法的方法原理作为开篇第一个方法,会夹带一些数字信号处理的基本方法,可能会导致篇幅比较啰嗦,之后几章我会尽量挑重点的讲解。 滑动平均法(moving average)也叫做移动平均法、平均法、移动平均值滤波法等等,是一种时间域思想上的信号光滑方法。算法思路为,将该点附近的采样点做算数平均,作为这个点光滑后的值。 matlab有两个函数实现滑动平均法,一个是smoothdata()函数,一个是movmean()函数。 以窗口长度为5为例,smoothdata()函数调用方法为: y = smoothdata( x , 'movmean' , 5 );但是这个smoothdata函数实际上是调用了movmean()函数。所以如果直接使用的话,直接用movmean()会更快。 movmean()函数的调用方法为: y = movmean( x , 5 );下面以一个加噪声的正弦信号为例: %移动平均滤波 clear clc close all N_window = 5;%窗口长度(最好为奇数) t = 0:0.1:10; A = cos(2*pi*0.5*t)+0.3*rand(size(t)); B1 = movmean(A,N_window); figure(1) plot(t,A,t,B1)
根据之前的公式,我们可以看到 y ( n ) = 1 / 3 ∗ ( x ( n − 1 ) + x ( n ) + x ( n + 1 ) ) y(n)=1/3*( x(n-1)+x(n)+x(n+1) ) y(n)=1/3∗(x(n−1)+x(n)+x(n+1)) 就相当于一个对x和向量[1/3 1/3 1/3]做卷积。 可以验证: N_window = 5;%窗口长度(最好为奇数) t = 0:0.25:10;%时间 A = cos(2*pi*0.5*t)+0.3*rand(size(t)); B1 = movmean(A,N_window); F_average = 1/N_window*ones(1,N_window);%构建卷积核 B2 = conv(A,F_average,'same');%利用卷积的方法计算 figure(2) plot(t,B1,t,B2)
首先介绍一下Z变换。以向前的滑动平均为例(这里中间值不是n而是n+1,所以相位会移动)。 y ( n ) = 1 / 3 ∗ ( x ( n ) + x ( n + 1 ) + x ( n + 2 ) ) y(n)=1/3*( x(n)+x(n+1)+x(n+2) ) y(n)=1/3∗(x(n)+x(n+1)+x(n+2)) 它的Z变换可以简单的理解为,把x(n+k)替换为z^(-k),即 H ( z ) = 1 3 ( z 0 + z − 1 + z − 2 ) H(z)=\frac{1}{3}(z^{0}+z^{-1}+z^{-2}) H(z)=31(z0+z−1+z−2) 因此对于filter滤波函数,输入的格式为: y = filter(b,a,x)其中b和a的定义为: H ( z ) = b 1 + b 2 ⋅ z − 1 + b 3 ⋅ z − 2 + ⋯ + b n ⋅ z − n + 1 1 + a 2 ⋅ z − 1 + a 3 ⋅ z − 2 + ⋯ + a m ⋅ z − m + 1 H(z)=\frac{b_1+b_2\cdot z^{-1}+b_3\cdot z^{-2}+\cdots +b_{n}\cdot z^{-n+1}}{1+a_2\cdot z^{-1}+a_3\cdot z^{-2}+\cdots +a_{m}\cdot z^{-m+1}} H(z)=1+a2⋅z−1+a3⋅z |
【本文地址】
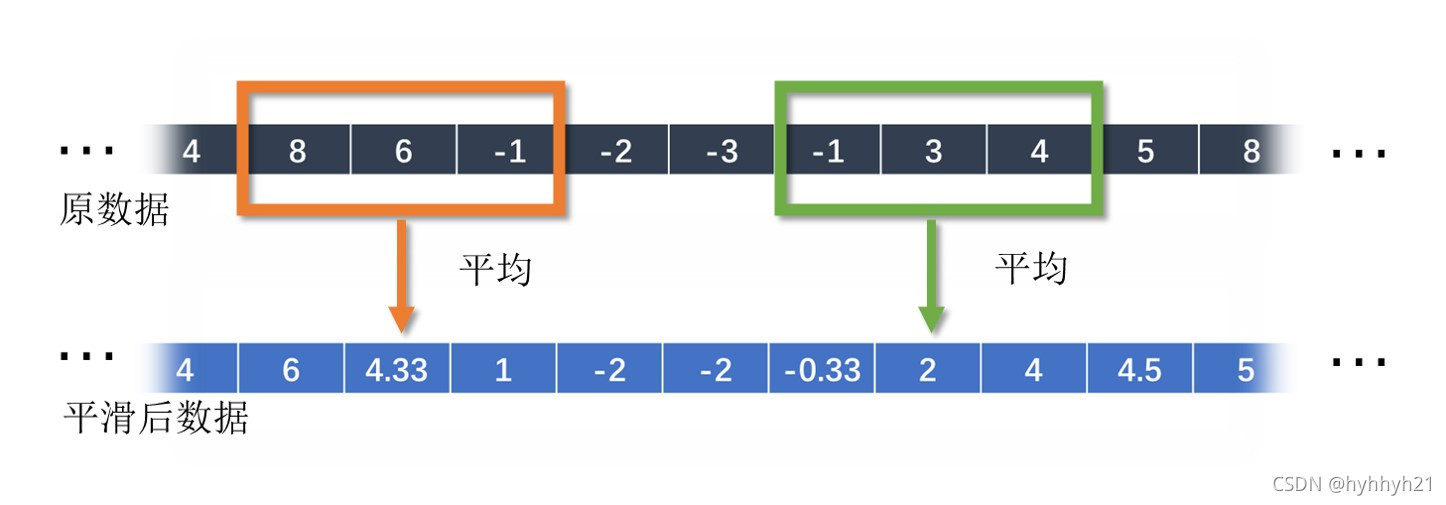 一般窗口为对称窗口,防止出现相位偏差。窗口一般为奇数。 以3点平均(窗口长度为3)公式为例,原数据为x,平滑后的数据为y: y ( n ) = 1 / 3 ∗ ( x ( n − 1 ) + x ( n ) + x ( n + 1 ) ) y(n)=1/3*( x(n-1)+x(n)+x(n+1) ) y(n)=1/3∗(x(n−1)+x(n)+x(n+1)) 对y(n)和y(n+1)相减,可以得到另一种计算形式: y ( n + 1 ) = y ( n ) − 1 3 x ( n − 1 ) + 1 3 x ( n + 2 ) y(n+1)=y(n)-\frac{1}{3}x(n-1)+\frac{1}{3}x(n+2) y(n+1)=y(n)−31x(n−1)+31x(n+2) 当然这两者都是等价的。
一般窗口为对称窗口,防止出现相位偏差。窗口一般为奇数。 以3点平均(窗口长度为3)公式为例,原数据为x,平滑后的数据为y: y ( n ) = 1 / 3 ∗ ( x ( n − 1 ) + x ( n ) + x ( n + 1 ) ) y(n)=1/3*( x(n-1)+x(n)+x(n+1) ) y(n)=1/3∗(x(n−1)+x(n)+x(n+1)) 对y(n)和y(n+1)相减,可以得到另一种计算形式: y ( n + 1 ) = y ( n ) − 1 3 x ( n − 1 ) + 1 3 x ( n + 2 ) y(n+1)=y(n)-\frac{1}{3}x(n-1)+\frac{1}{3}x(n+2) y(n+1)=y(n)−31x(n−1)+31x(n+2) 当然这两者都是等价的。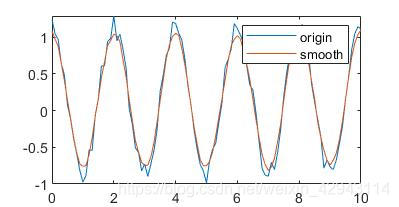
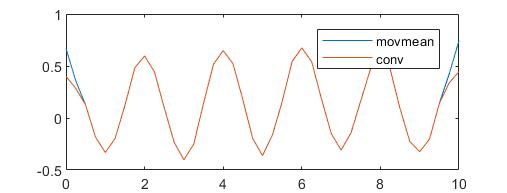 中间部分两者完全一致,但是两端有所差别。主要是因为,movmean()函数在处理边缘时,采用减小窗口的方式,而conv()相当于在两端补零。所以如何处理边缘也是值得注意的。
中间部分两者完全一致,但是两端有所差别。主要是因为,movmean()函数在处理边缘时,采用减小窗口的方式,而conv()相当于在两端补零。所以如何处理边缘也是值得注意的。