5.4.2 正弦函数、余弦函数的性质2 (单调性与最值) |
您所在的位置:网站首页 › 正弦函数的最大值最小值怎么算 › 5.4.2 正弦函数、余弦函数的性质2 (单调性与最值) |
5.4.2 正弦函数、余弦函数的性质2 (单调性与最值)
|
\({\color{Red}{欢迎到学科网下载资料学习 }}\) 【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019) \({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\) 必修第一册同步巩固,难度2颗星! 基础知识 正弦函数,余弦函数的图像与性质注 表中的\(k∈Z\) \(y=\sin x\) \(y=\cos x\) 图像
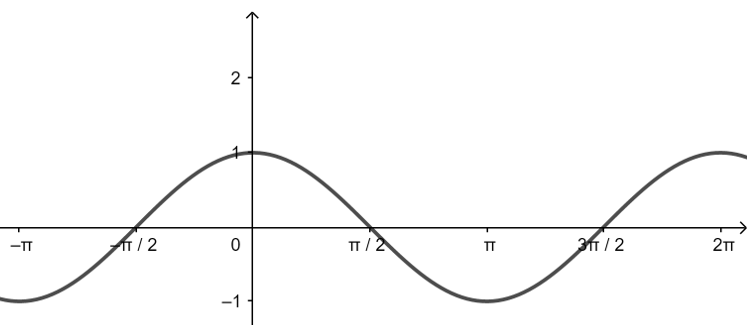 定义域
\(R\)
\(R\)
值域
\(\left[-1 ,1\right]\)
\(\left[-1 ,1\right]\)
周期性
\(2π\)
\(2π\)
对称中心
\((kπ ,0)\)
\(\left(kπ+\dfrac{\pi}{2},0\right)\)
对称轴
\(x=kπ+\dfrac{\pi}{2}\)
\(x=kπ\)
单调性
在\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)上是增函数;在\(\left[\dfrac{\pi}{2}+2kπ ,3\dfrac{\pi}{2}+2kπ\right]\)上是减函数.
在\(\left[-π+2kπ ,2kπ\right]\)上是增函数;在\(\left[2kπ ,π+2kπ\right]\)上是减函数.
最值
当\(x=\dfrac{\pi}{2}+2kπ\)时,\(y_{\max}=1\);当\(x=-\dfrac{\pi}{2}+2kπ\)时,\(y_{\min}=-1\).
当\(x=2kπ\)时,\(y_{\max}=1\);当\(x=π+2kπ\)时,\(y_{\min}=-1\).
定义域
\(R\)
\(R\)
值域
\(\left[-1 ,1\right]\)
\(\left[-1 ,1\right]\)
周期性
\(2π\)
\(2π\)
对称中心
\((kπ ,0)\)
\(\left(kπ+\dfrac{\pi}{2},0\right)\)
对称轴
\(x=kπ+\dfrac{\pi}{2}\)
\(x=kπ\)
单调性
在\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)上是增函数;在\(\left[\dfrac{\pi}{2}+2kπ ,3\dfrac{\pi}{2}+2kπ\right]\)上是减函数.
在\(\left[-π+2kπ ,2kπ\right]\)上是增函数;在\(\left[2kπ ,π+2kπ\right]\)上是减函数.
最值
当\(x=\dfrac{\pi}{2}+2kπ\)时,\(y_{\max}=1\);当\(x=-\dfrac{\pi}{2}+2kπ\)时,\(y_{\min}=-1\).
当\(x=2kπ\)时,\(y_{\max}=1\);当\(x=π+2kπ\)时,\(y_{\min}=-1\).
解释 如何理解三角函数的单调性、最值? 主要是结合图象及其周期性,比如如何理解正弦函数\(f(x)=\sin x\)在\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)单调递增? ① 在一个周期\(\left[-\dfrac{\pi}{2},\dfrac{3\pi}{2}\right)\)内,找到一个单调增区间\(\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\); ② 接着每隔一个周期\(2π\)个单位就有一个增区间,则\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)是\(f(x)=\sin x\)的增区间. 类似可得到正弦函数的减区间与最值,余弦函数的单调性与最值. (也可以利用单位圆的性质研究正弦函数、余弦函数的性质) 【例】 求正弦函数\(f(x)=\sin x\)、余弦函数\(f(x)=\cos x\)在\(\left[0,2π\right]\)的单调性. 解 结合图象可得,正弦函数\(f(x)=\sin x\)的增区间是\(\left[0,\dfrac{\pi}{2}\right)\),\(\left[\dfrac{3\pi}{2},2π\right]\),减区间是\(\left[\dfrac{\pi}{2},\dfrac{3\pi}{2}\right]\); 余弦函数\(f(x)=\cos x\)的增区间是\(\left(π,2π\right]\),减区间是\([0,π)\). 基本方法 【题型1】 单调性【典题1】 求下列函数的单调递减区间. (1) \(y=\cos \left(2x+\dfrac{\pi}{3}\right)\);$\qquad \qquad $ (2)\(y=2\sin \left(\dfrac{\pi}{4}-x\right)\). 解析 (1) 令\(z=2x+\dfrac{\pi}{3}\),而函数\(y=\cos z\) 的递减区间是\(\left[2kπ,2kπ+π\right](k∈Z)\). \(\therefore\)原函数递减时,可得\(2kπ≤2x+\dfrac{\pi}{3}≤2kπ+π(k∈Z)\), 解得\(kπ-\dfrac{\pi}{6}≤x≤kπ+\dfrac{\pi}{3}(k∈Z)\). \(\therefore\) 原函数的递减区间是\(\left[kπ-\dfrac{\pi}{6},kπ+\dfrac{\pi}{3}\right](k∈Z)\). (2)\(y=2\sin \left(\dfrac{\pi}{4}-x \right)=-2\sin \left(x-\dfrac{\pi}{4} \right)\), 令\(z=x-\dfrac{\pi}{4}\), 而函数\(y=-2\sin z\)的递减区间是\(\left[2kπ-\dfrac{\pi}{2},2kπ+\dfrac{\pi}{2}\right](k∈Z)\). \(\therefore\) 原函数递减时,得\(2kπ-\dfrac{\pi}{2}≤x-\dfrac{\pi}{4}≤2kπ+\dfrac{\pi}{2}(k∈Z)\), 得\(2kπ-\dfrac{\pi}{4}≤x≤2kπ+\dfrac{3\pi}{4}(k∈Z)\). \(\therefore\)原函数的递减区间是\(\left[2kπ-\dfrac{\pi}{4},2kπ+\dfrac{3\pi}{4}\right](k∈Z)\). 点拨 求三角函数\(f(x)=A\sin (ωx+φ)(ω>0)\)的单调性,利用换元法\(z=ωx+φ\),把\(ωx+φ\)代入\(y=\sin z\)对应的单调区间;而由复合函数的单调性“同增异减”,\(y=2\sin \left(\dfrac{\pi}{4}-x \right)\)与\(y=2\sin \left(x-\dfrac{\pi}{4} \right)\)的单调性相反. 【典题2】 下列关系式中正确的是( ) A.\(\sin 11°0,|φ|0,0 |
【本文地址】
今日新闻 |
推荐新闻 |