基于Matlab的B |
您所在的位置:网站首页 › 样条插值法补充数据是什么 › 基于Matlab的B |
基于Matlab的B
|
(已对代码部分进行调整和修改,谢谢大家的提醒!) 1. 原理介绍
B B B-样条插值法是一种利用分段多项式函数来逼近给定数据点的方法。 B B B-样条插值法的优点是可以构造出光滑且连续可微的曲线,而且可以通过调整控制点的位置来改变曲线的形状。 B B B-样条曲线由一组控制点和一组节点矢量定义。控制点是曲线上的点,而节点矢量是定义基函数的参数。节点矢量的选取方法有多,包括均匀参数法、积累弦长法和向心参数法。 均匀参数法:将参数区间平均划分为等距的子区间。积累弦长法:参数的划分与数据点之间的距离成正比。向心参数法:参数的划分与数据点之间的距离的平方根成正比。B B B-样条插值法的基本思想是,给定 n n n个数据点,我们要找到一条曲线,使得它在每个数据点处的函数值和导数值都与数据点相符。为了实现这个目标,我们首先要确定一组控制点,然后用一种称为B-样条基函数的特殊函数来表示曲线。 B B B-样条基函数的性质是,它只在有限的区间内非零,而且可以任意调节其阶数和平滑度。通过将不同的 B B B-样条基函数加权求和,我们就可以得到 B B B-样条插值曲线1。 假设我们要构造三次 B B B-样条插值曲线,也就是说,每个分段的曲线都是三次多项式函数。那么,我们需要确定 m m m 个控制点,记为 P 0 , P 1 , … , P m − 1 {P_0},{P_1}, \ldots ,{P_{m - 1}} P0,P1,…,Pm−1. ,以及一个参数 t t t,表示曲线上的位置。我们可以用下面的公式来表示 B B B-样条插值曲线: P ( t ) = ∑ i = 0 m − 1 p i N i , 3 ( t ) P\left( t \right) = \sum\limits_{i = 0}^{m - 1} {{p_i}{N_{i,3}}\left( t \right)} P(t)=i=0∑m−1piNi,3(t) 其中, p i {p_i} pi 是控制点的坐标向量, N i , 3 ( t ) {N_{i,3}}\left(t\right) Ni,3(t)是三次B-样条基函数,它的定义如下: N i , 0 ( t ) = { 1 , i f t i ≤ t ≤ t i + 1 0 , o t h e r w i s e {N_{i,0}}\left( t \right) = \left\{ \begin{array}{l} 1, & if & {t_i} \le t \le {t_{i + 1}}\\ 0, & otherwise \end{array} \right. Ni,0(t)={1,0,ifotherwiseti≤t≤ti+1 N i , k ( t ) = t − t i t i + k − t i N i , k − 1 ( t ) + t i + k + 1 − t t i + k + 1 − t i + 1 N i + 1 , k − 1 ( t ) {N_{i,k}}\left( t \right) = \frac{{t - {t_i}}}{{{t_{i + k}} - {t_i}}}{N_{i,k - 1}}\left( t \right) + \frac{{{t_{i + k + 1}} - t}}{{{t_{i + k + 1}} - {t_{i + 1}}}}{N_{i + 1,k - 1}}\left( t \right) Ni,k(t)=ti+k−tit−tiNi,k−1(t)+ti+k+1−ti+1ti+k+1−tNi+1,k−1(t) 这里, t i t_i ti 是一组称为节点的数,它们满足 t 0 ≤ t 1 ≤ . . . ≤ t m + 2 {t_0} \le {t_1} \le ... \le {t_{m + 2}} t0≤t1≤...≤tm+2 ,并且 t 0 = t 3 {t_0} = {t_3} t0=t3 t m − 1 = t m + 2 {t_{m - 1}} = {t_{m + 2}} tm−1=tm+2 。 节点的作用是划分曲线的分段区间,以及控制曲线的形状。一般来说,节点的选择可以根据数据点的分布或者其他的标准来确定。 为了计算 B B B-样条插值曲线,我们还需要知道控制点的坐标。这可以通过求解一个线性方程组来实现。假设我们有 n n n 个数据点,记为 X 0 , X 1 , . . . , X n − 1 {X_0},{X_1},...,{X_{n - 1}} X0,X1,...,Xn−1,并且已经确定了节点 t 0 , t 1 , . . . , t m + 2 {t_0},{t_1},...,{t_{m + 2}} t0,t1,...,tm+2,那么我们可以将数据点和曲线的关系写成如下的形式: X j = ∑ i = 0 m − 1 p i N i , 3 ( t j ) , j = 0 , 1 , . . . , n − 1 {X_j} = \sum\limits_{i = 0}^{m - 1} {{p_i}} {N_{i,3}}({t_j}),\quad j = 0,1,...,n - 1 Xj=i=0∑m−1piNi,3(tj),j=0,1,...,n−1 其中, t j {t_j} tj 是数据点 X j {X_j} Xj对应的参数值,它可以通过一些方法来估计,例如均匀分布,弦长分布,或者最优化分布等。将上面的方程写成矩阵形式,我们有: X = N P X = NP X=NP 其中, X X X 是一个 n × d n \times d n×d 的矩阵, 表示数据点的坐标, d d d 是空间维度; N {N} N是一个 n × m n \times m n×m 的矩阵,表示 B B B-样条基函数的值; P {P} P 是一个 m × d m \times d m×d 的矩阵,表示控制点的坐标。如果 N {N} N 是非奇异的,那么我们可以直接求解 P {P} P: P = N − 1 X {P} = {N}^{-1} {X} P=N−1X 如果 N {N} N 是奇异的,那么我们可以用最小二乘法来求解 P {P} P,使得曲线和数据点的距离平方和最小: P = ( N T N ) − 1 N T X {P} = ( {N}^T {N})^{-1} {N}^T {X} P=(NTN)−1NTX 这样,我们就得到了 B B B-样条插值曲线的控制点,从而可以计算出曲线上任意一点的坐标。 2. 具体实例以一个具体实际问题举例。 首先来建个模: 对于一个船舶的航迹规划问题,为了建立航迹规划模型,首先得对洋流进行建模。
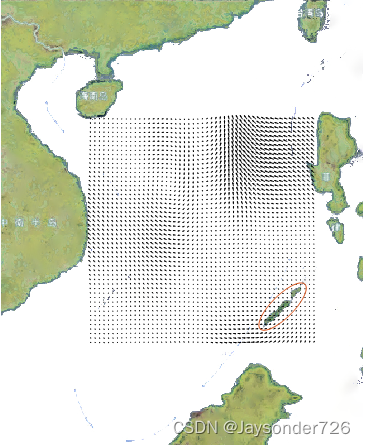
洋流数据分为 x x x, y y y, u u u, v v v四个维度,其中 x x x, y y y为洋流的位置坐标, u u u, v v v为洋流的速度坐标。 建立洋流的速度方程: u = u ( x , y ) u=u\left( x,y \right) u=u(x,y) v = v ( x , y ) v=v\left(x,y\right) v=v(x,y) 从官网上下载了洋流数据后,由于洋流数据不平滑,不方便后续的算法的解析处理,需要对洋流进行平滑处理。 为了减小数据中的噪声,需要采用 B B B-样条插值法对洋流数据进行平滑处理。通过调整 B B B-样条的阶数和节点数,可以有效地降低数据中的高频噪声,提高数据的可用性。 再重复一下重点,加深印象: B B B-样条插值法的目的是为给定的离散数据点生成一条光滑的曲线。它的基本思想是通过将一组基函数(B-样条基函数)与一组控制点相乘并求和来构造曲线。通过调整控制点的位置,可以实现对曲线形状的局部控制。 在上面所给的公式计算了 B-样条的基函数后,可以通过求解线性方程组来求解控制点,首先,由插值条件确定的方程如下2: C 3 ( α ) = ∑ j = i − 3 i N j , 3 ( α i ) P j = D j − 3 {C_3}\left( \alpha \right) = \sum\limits_{j = i - 3}^i {{N_{j,3}}\left( {{\alpha _i}} \right)} {P_j} = {D_{j - 3}} C3(α)=j=i−3∑iNj,3(αi)Pj=Dj−3 i = 3 , 4 , … , n + 1 i = 3,4, \ldots ,n + 1 i=3,4,…,n+1 其中, D j − 3 {D_{j - 3}} Dj−3为一组型值点。 由于节点向量 A = { α 0 , α 1 , … , α m } {\rm A} = \left\{ {{\alpha _0},{\alpha _1}, \ldots ,{\alpha _m}} \right\} A={α0,α1,…,αm}的首末节点分别为4重,即 α 0 = α 1 = α 2 = α 3 = 0 {\alpha _0} = {\alpha _1} = {\alpha _2} = {\alpha _3} = 0 α0=α1=α2=α3=0, α m − 3 = α m − 2 = α m − 1 = α m = 1 {\alpha _{m - 3}} = {\alpha _{m - 2}} = {\alpha _{m - 1}} = {\alpha _m} = 1 αm−3=αm−2=αm−1=αm=1,故方程有 n + 1 n + 1 n+1个未知数, n − 1 n-1 n−1个方程,矩阵方程无解,故需要补充两个方程,使解空间的维度匹配。将首末型值点分别与参数 ε 1 ∈ [ α 3 , α 4 ] {\varepsilon _1} \in \left[ {{\alpha _3},{\alpha _4}} \right] ε1∈[α3,α4]和参数 ε 2 ∈ [ α n , α n + 1 ] {\varepsilon _2} \in \left[ {{\alpha _n},{\alpha _{n + 1}}} \right] ε2∈[αn,αn+1]上的点对应,使设定的参数趋近于 α 3 {\alpha _3} α3h\和 α n {\alpha _n} αn,得: P 0 N 0 , 3 ( ε 1 ) + P 1 N 1 , 3 ( ε 1 ) + P 2 N 2 , 3 ( ε 1 ) + P 3 N 3 , 3 ( ε 1 ) = D 0 {P_0}{N_{0,3}}\left( {{\varepsilon _1}} \right) + {P_1}{N_{1,3}}\left( {{\varepsilon _1}} \right) + {P_2}{N_{2,3}}\left( {{\varepsilon _1}} \right) + {P_3}{N_{3,3}}\left( {{\varepsilon _1}} \right) = {D_0} P0N0,3(ε1)+P1N1,3(ε1)+P2N2,3(ε1)+P3N3,3(ε1)=D0 P n − 3 N n − 3 , 3 ( ε 2 ) + P n − 2 N n − 2 , 3 ( ε 2 ) + P n − 1 N n − 1 , 3 ( ε 2 ) + P n N n , 3 ( ε 2 ) = D n − 2 {P_{n - 3}}{N_{n - 3,3}}\left( {{\varepsilon _2}} \right) + {P_{n - 2}}{N_{n - 2,3}}\left( {{\varepsilon _2}} \right) + {P_{n - 1}}{N_{n - 1,3}}\left( {{\varepsilon _2}} \right) + {P_n}{N_{n,3}}\left( {{\varepsilon _2}} \right) = {D_{n - 2}} Pn−3Nn−3,3(ε2)+Pn−2Nn−2,3(ε2)+Pn−1Nn−1,3(ε2)+PnNn,3(ε2)=Dn−2 通过联立以上方程得到一个矩阵方程,利用追赶法求得控制点。 通过控制点和基函数,便可以确定对应区间的3次B-样条插值的具体曲线方程。 在下面所给代码中,选择采用 3 3 3 次 B-样条曲线, 对于给定的离散数据点,首先要计算参数向量。在本代码中,采用积累弦长法计 算参数向量。具体来说,计算每两个相邻数据点之间的距离,并将所有距离累加,然后将累加的距离归一化到 [ 0 , 1 ] [0,1] [0,1]区间,作为参数向量3。 接下来,需要计算节点矢量。在本代码中,采用 3 3 3 次 B-样条曲线,所以节点矢量的长度为 m = n + 1 + r m = n +1+ r m=n+1+r ,其中 r r r 为控制点的数量。根据节点矢量的选取规则,可以使用以下方法生成节点矢量: 前n +1个节点设置为 0;最后n +1个节点设置为 1;中间的节点按照参数向量的值平均分布。之后,需要计算控制点。可以使用数值方法(如高斯消元法、LU 分解等)来求 解式(2.5), (2.6)和(2.7)联立得到的线性方程组,得到控制点向量 P 。通过求解控制点 和基函数,从而求得样条插值函数。 代码如下: 主函数: %% 洋流建模与预处理 V = 3.5; % 测试洋流的航行速度 V0 = 6; % 测试洋流的航行速度3 V1 = 5.5; % 实际洋流的航行速度 C = 3; % 最快洋流速度 h = 1/260; % 洋流建模系数 x0 = [160 216]'; % 起始点位置 x0_1 = x0(1); % 起始点位置的x坐标 x0_2 = x0(2); % 起始点位置的y坐标 x111 = [560 616]'; % 终点位置(对比) x11 = [560 616]'; % 终点位置 ax = [0.8*200,2.8*200,1.08*200,3.08*200]; % 洋流区域建模 TT = 0:0.01:2*pi; % 约束参数方程的自变量建模 %Construct a struct to store parameters para = struct('x0',x0,'x11',x11,'x111',x111,'V',V,'V0',V0,'C',C,'h',h); %结构体建模 %%%%%%__将实际洋流用B-样条插值进行平滑处理___%%%%%%% X = [-0.70, 1.70, -0.50, -0.10, -1.00, -4.10, -2.50, -1.90, -0.30, -3.60; -4.70, 2.40, -1.00, 16.60, -2.20, 16.40, -25.90, -32.20, -18.30,-18.40; -28.80, -5.60, -7.10, -21.10, -9.60, 3.50, 5.50, 1.40, 0.70, 3.40; 5.90, 1.20, 1.70, -1.90, 4.80, 0.70, -0.10, 3.60, 0.30, -0.70; -2.10, 2.50, -0.60, -2.80, -10.80, 18.90, 34.00, 17.80, 3.50, 6.20]; Y = [-11.30, -2.20, -3.80, -3.00, -8.10, 0.50, -10.30, 0.20, 4.30, -0.40; -0.30, -2.30, 5.10, -3.00, 19.50, -18.90, -34.20, -7.00, -15.20, -19.00; -18.30, -9.90, -8.60, -13.00, 6.30,2.90, -3.20, 3.40, 0.30, 1.80; -1.50, 4.30, -4.40, -0.90, -2.90, 5.50, -1.20, 4.10, 1.40, 0.30; -1.90, 2.90, 2.20, -0.70, -4.80, 2.20, 3.10, -18.10, -19.50, -4.00]; Z = [11.30, 2.80, 3.80, 3.00, 8.20, 4.10, 10.60, 1.90, 4.30, 3.60; 4.70, 3.30, 5.20, 16.90, 19.60, 25.00, 42.90, 33.00, 23.80, 26.40; 34.10, 11.40, 11.20, 24.80, 11.50, 4.50, 6.40, 3.70, 0.80, 3.80; 6.10, 4.50, 4.70, 2.10, 5.60, 5.50, 1.20, 5.50, 1.40, 0.80; 2.80, 3.80, 2.30, 2.90, 11.80, 19.00, 34.10, 25.40, 19.80,7.40]; [M, N] = size(X); global FLAG_U FLAG_V; FLAG_U = 1; FLAG_V = 1; k = 2; l = 2; [uu,vv,zz]=Surf_PlotSubMesh(M, N, k, l, X, Y, Z); [xx,yy] = meshgrid(linspace(ax(1),ax(2),51),linspace(ax(3),ax(4),51)); %%%%%%%%%_用最小二乘法将uu方向的洋流拟合成二维曲线方程_%%%%%%%%%%%%% [n,m]=size(uu);%assumes that d is a n x m matrix % [XX,YY]=meshgrid(1:n,1:m);%your x-y coordinates [XX,YY] = meshgrid(linspace(ax(1),ax(2),51),linspace(ax(3),ax(4),51)); xxx(:,1)=XX(:); % x= first column xxx(:,2)=YY(:); % y= second column f=uu(:); % your data f(x,y) (in column vector) %--- now define the function in terms of x %--- where you use xxx(:,1)=X and xxx(:,2)=Y fun = @(c1,xxx) c1(1)*sin(c1(3)*(xxx(:,1)-x0_1)/8+c1(2)*pi)+c1(4)*((xxx(:,2)-x0_2)/8).^2; %--- now solve with lsqcurvefit options=optimset('TolX',1e-6); c0=[1 0.5 0 1];%start-guess here cc1=lsqcurvefit(fun,c0,xxx,f,[],[],options); Ifit=fun(cc1,xxx); Ifit=reshape(Ifit,[n m]);%fitting data reshaped as matrix figure(7) surf(XX,YY,Ifit) hold on plot3(XX,YY,uu) hold off % plot3(XX, YY, dataArray); %%%%%%%%%_用最小二乘法将vv方向的洋流拟合成二维曲线方程_%%%%%%%%%%%%%%%% [n,m]=size(vv);%assumes that d is a n x m matrix % [XX,YY]=meshgrid(1:n,1:m);%your x-y coordinates xxy(:,1)=XX(:); % x= first column xxy(:,2)=YY(:); % y= second column f=vv(:); % your data f(x,y) (in column vector) %--- now define the function in terms of x %--- where you use xxy(:,1)=X and xxy(:,2)=Y % fun = @(c2,xxy) c2(1)*sin(c2(3)*xxy(:,1)+c2(2)*pi).^2.*cos(c2(4)*xxy(:,2)+c2(5)*pi)+c2(7)*sin(c2(8)*xxy(:,1))+c2(6)*xxy(:,2).^4; fun = @(c2,xxy) c2(1)*sin(c2(3)*(xxy(:,1)-x0_1)/8+c2(2)*pi)+c2(4)*((xxy(:,2)-x0_2)/8).^2; %--- now solve with lsqcurvefit options=optimset('TolX',1e-6); % c02=[1 0.5 0.5 0.5 0.8 0.5 0.4 0.5];%start-guess here c02=[1 0.5 0.5 0.5];%start-guess here % c02=[1 0.5 0 0.5]; cc2=lsqcurvefit(fun,c02,xxy,f,[],[],options); Ifit_1=fun(cc2,xxy); Ifit_1=reshape(Ifit_1,[n m]);%fitting data reshaped as matrix figure(8) surf(XX,YY,Ifit_1) hold on plot3(XX,YY,vv) hold off3次B-样条插值函数: function [X_MN_piece,Y_MN_piece,Z_MN_piece]=Surf_PlotSubMesh(M, N, k, l, X, Y, Z) % 绘制网格曲面,X Y Z是所绘制的M*N网格的坐标,k, l是网格的u向和v向的次数 global FLAG_U FLAG_V; % ------------------------------------------------------------------ % 根据所选择的类型绘图 n = N - 1; m = M - 1; piece_u = 51; % u向的节点矢量细分 piece_v = 51; Nik_u = zeros(n+1, 1); % 基函数初始化 Nik_v = zeros(m+1, 1); % u方向的细分 switch FLAG_U case 1 NodeVector_u = linspace(0, 1, n+k+2); % 均匀B样条的u向节点矢量 u = linspace(k/(n+k+1), (n+1)/(n+k+1), piece_u); % u向节点分成若干份 X_M_piece = zeros(M, piece_u); % 沿着u方向的网格,M * piece Y_M_piece = zeros(M, piece_u); Z_M_piece = zeros(M, piece_u); for i = 1 : M for j = 1 : piece_u for ii = 0 : 1: n Nik_u(ii+1, 1) = BaseFunction(ii, k , u(j), NodeVector_u); end X_M_piece(i, j) = X(i, :) * Nik_u; Y_M_piece(i, j) = Y(i, :) * Nik_u; Z_M_piece(i, j) = Z(i, :) * Nik_u; end end case 2 NodeVector_u = U_quasi_uniform(n, k); % 准均匀B样条的u向节点矢量 u = linspace(0, 1-0.0001, piece_u); %% u向节点分成若干份 X_M_piece = zeros(M, piece_u); % 沿着u方向的网格,M * piece Y_M_piece = zeros(M, piece_u); Z_M_piece = zeros(M, piece_u); for i = 1 : M for j = 1 : piece_u for ii = 0 : 1: n Nik_u(ii+1, 1) = BaseFunction(ii, k , u(j), NodeVector_u); end X_M_piece(i, j) = X(i, :) * Nik_u; Y_M_piece(i, j) = Y(i, :) * Nik_u; Z_M_piece(i, j) = Z(i, :) * Nik_u; end end case 3 if ~mod(n, k) NodeVector_u = U_piecewise_Bezier(n, k); % 分段Bezier曲线的节点矢量 u = linspace(0, 1-0.0001, piece_u); %% u向节点分成若干份 X_M_piece = zeros(M, piece_u); % 沿着u方向的网格,M * piece_u Y_M_piece = zeros(M, piece_u); Z_M_piece = zeros(M, piece_u); for i = 1 : M for j = 1 : piece_u for ii = 0 : 1: n Nik_u(ii+1, 1) = BaseFunction(ii, k , u(j), NodeVector_u); end X_M_piece(i, j) = X(i, :) * Nik_u; Y_M_piece(i, j) = Y(i, :) * Nik_u; Z_M_piece(i, j) = Z(i, :) * Nik_u; end end else errordlg('Error: n/k is not an integer!', 'Piecewise Bezier'); end otherwise % NodeVector_u = U_Hartley_Judd(n, k, P); % Hartley-Judd方法 u = linspace(0, 1-0.0001, piece_u); %% u向节点分成若干份 X_M_piece = zeros(M, piece_u); % 沿着u方向的网格,M * piece Y_M_piece = zeros(M, piece_u); Z_M_piece = zeros(M, piece_u); for i = 1 : M % ------------------------------------------------------------- % 计算第i行控制顶点的节点矢量 Points = zeros(3, n+1); Points(1, :) = X(i, :); Points(2, :) = Y(i, :); Points(3, :) = Z(i, :); NodeVector_u = zeros(1, n+k+2); % 节点矢量长度为n+k+2 NodeVector_u(1, n+2 : n+k+2) = ones(1, k+1); % 右端节点置1 Len = zeros(1, n); % 控制多边形共n条边 for iP = 2 : n+1 Len(iP-1) = sqrt((Points(1,iP) - Points(1,iP-1))^2 ... + (Points(2,iP) - Points(2,iP-1))^2 ... + (Points(3,iP) - Points(3,iP-1))^2); end Lsum = 2*sum(Len) - Len(1) - Len(n); for iP = k+2 : n+1 NodeVector_u(1, iP) = (2*sum( Len(1 : iP-2) ) - Len(1) - Len(iP-2)) / Lsum; end % ------------------------------------------------------------- for j = 1 : piece_u for ii = 0 : 1: n Nik_u(ii+1, 1) = BaseFunction(ii, k , u(j), NodeVector_u); end X_M_piece(i, j) = X(i, :) * Nik_u; Y_M_piece(i, j) = Y(i, :) * Nik_u; Z_M_piece(i, j) = Z(i, :) * Nik_u; end end end % v方向的细分 switch FLAG_V case 1 NodeVector_v = linspace(0, 1, m+l+2); % 均匀B样条的u向节点矢量 v = linspace(l/(m+l+1), (m+1)/(m+l+1), piece_v); % v向节点分成若干份 X_MN_piece = zeros(piece_v, piece_u); Y_MN_piece = zeros(piece_v, piece_u); Z_MN_piece = zeros(piece_v, piece_u); for i = 1 : piece_u for j = 1 : piece_v for ii = 0 : 1 : m Nik_v(ii+1, 1) = BaseFunction(ii, l, v(j), NodeVector_v); end X_MN_piece(j, i) = Nik_v' * X_M_piece(:, i); Y_MN_piece(j, i) = Nik_v' * Y_M_piece(:, i); Z_MN_piece(j, i) = Nik_v' * Z_M_piece(:, i); end end case 2 NodeVector_v = U_quasi_uniform(m, l); % 准均匀B样条的v向节点矢量 v = linspace(0, 1-0.0001, piece_v); % v向节点分成若干份 X_MN_piece = zeros(piece_v, piece_u); Y_MN_piece = zeros(piece_v, piece_u); Z_MN_piece = zeros(piece_v, piece_u); for i = 1 : piece_u for j = 1 : piece_v for ii = 0 : 1 : m Nik_v(ii+1, 1) = BaseFunction(ii, l, v(j), NodeVector_v); end X_MN_piece(j, i) = Nik_v' * X_M_piece(:, i); Y_MN_piece(j, i) = Nik_v' * Y_M_piece(:, i); Z_MN_piece(j, i) = Nik_v' * Z_M_piece(:, i); end end case 3 if ~mod(m, l) NodeVector_v = U_piecewise_Bezier(m, l); % 分段Bezier的v向节点矢量 v = linspace(0, 1-0.0001, piece_v); % v向节点分成若干份 X_MN_piece = zeros(piece_v, piece_u); Y_MN_piece = zeros(piece_v, piece_u); Z_MN_piece = zeros(piece_v, piece_u); for i = 1 : piece_u for j = 1 : piece_v for ii = 0 : 1 : m Nik_v(ii+1, 1) = BaseFunction(ii, l, v(j), NodeVector_v); end X_MN_piece(j, i) = Nik_v' * X_M_piece(:, i); Y_MN_piece(j, i) = Nik_v' * Y_M_piece(:, i); Z_MN_piece(j, i) = Nik_v' * Z_M_piece(:, i); end end else errordlg('Error: n/k is not an integer!', 'Piecewise Bezier'); end otherwise % NodeVector_u = U_Hartley_Judd(n, k, P); % Hartley-Judd方法 v = linspace(0, 1-0.0001, piece_v); % v向节点分成若干份 X_MN_piece = zeros(piece_v, piece_u); % 沿v向的网格piece_v * piece_u Y_MN_piece = zeros(piece_v, piece_u); Z_MN_piece = zeros(piece_v, piece_u); for i = 1 : piece_u % ------------------------------------------------------------- % 计算第i行控制顶点的节点矢量 Points = zeros(3, m+1); Points(1, :) = X_M_piece(:, i)'; Points(2, :) = Y_M_piece(:, i)'; Points(3, :) = Z_M_piece(:, i)'; NodeVector_v = zeros(1, m+l+2); % 节点矢量长度为n+k+2 NodeVector_v(1, m+2 : m+l+2) = ones(1, l+1); % 右端节点置1 Len = zeros(1, m); % 控制多边形共n条边 for iP = 2 : m+1 Len(iP-1) = sqrt((Points(1,iP) - Points(1,iP-1))^2 ... + (Points(2,iP) - Points(2,iP-1))^2 ... + (Points(3,iP) - Points(3,iP-1))^2); end Lsum = 2*sum(Len) - Len(1) - Len(m); for iP = l+2 : m+1 NodeVector_v(1, iP) = (2*sum( Len(1 : iP-2) ) - Len(1) - Len(iP-2)) / Lsum; end % ------------------------------------------------------------- for j = 1 : piece_v for ii = 0 : 1: m Nik_v(ii+1, 1) = BaseFunction(ii, l, v(j), NodeVector_v); end X_MN_piece(j, i) = Nik_v' * X_M_piece(:, i); Y_MN_piece(j, i) = Nik_v' * Y_M_piece(:, i); Z_MN_piece(j, i) = Nik_v' * Z_M_piece(:, i); end end end function Nik_u = BaseFunction(i, k , u, NodeVector) % 计算基函数Ni,k(u),NodeVector为节点向量 if k == 0 % 0次B样条 if (u >= NodeVector(i+1)) && (u =1) % 满足n是k的整数倍且k为正整数 NodeVector = zeros(1, n+k+2); % 节点矢量长度为n+k+2 NodeVector(1, n+2 : n+k+2) = ones(1, k+1); % 右端节点置1 piecewise = n / k; % 设定内节点的值 Flg = 0; if piecewise > 1 for i = 2 : piecewise for j = 1 : k NodeVector(1, k+1 + Flg*k+j) = (i-1)/piecewise; end Flg = Flg + 1; end end else fprintf('error!\n'); end 3. 结果图
u
u
u方向: v v v方向:
De Boor, C. (1978). A practical guide to splines. Springer-Verlag ↩︎ Feng, Kai et al. “Path Optimization of Agricultural Robot Based on Immune Ant Colony: B-Spline Interpolation Algorithm.” Mathematical Problems in Engineering (2022): n. pag. ↩︎ Lee, S., Wolberg, G., & Shin, S. Y. (1997). Scattered data interpolation with multilevel B-splines. IEEE Transactions on Visualization and Computer Graphics, 3(3), 228–244 ↩︎ |
【本文地址】
今日新闻 |
推荐新闻 |

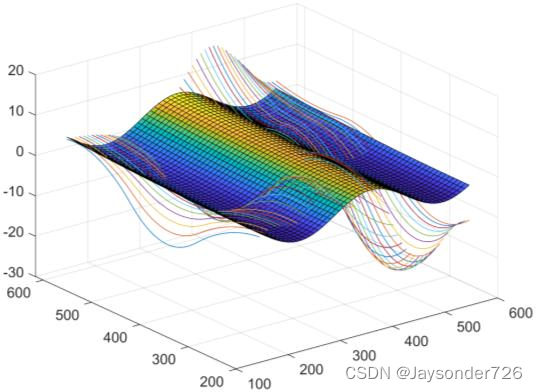
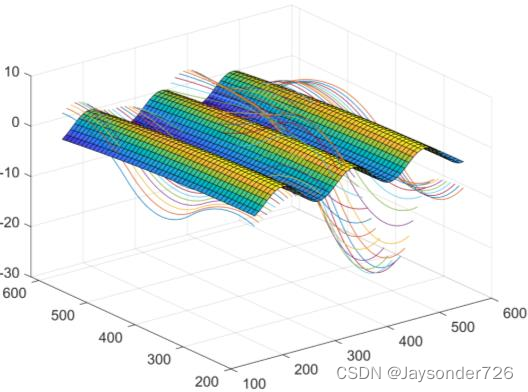 拟合效果(以南海洋流为样本):
拟合效果(以南海洋流为样本):