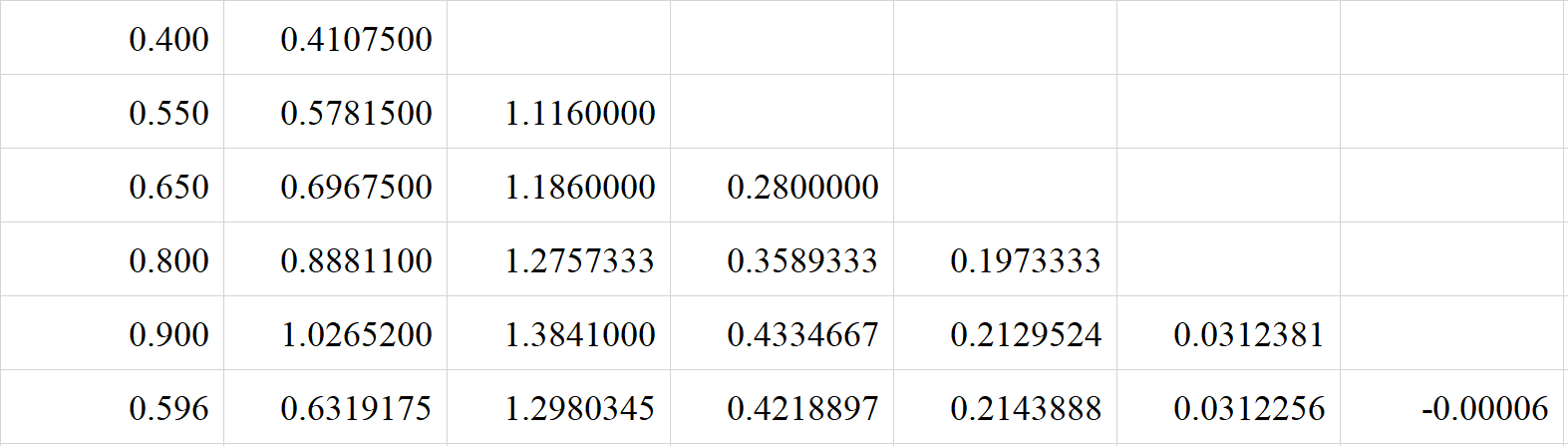
牛顿插值有两种表达形式：均差形式的牛顿插值和差分形式的牛顿插值。

第一种：均差形式的牛顿插值

只有各阶的均差我们是不知道的，但是我们可以通过构造均差表来求得。

并且值得注意的一点是：在高阶均差中的同阶均差相差不多，可以近似相等，这可以简化求误差限；同样也正是因为这个原因，我们在求误差限的时候通常是将\(f[x, x_0, x_1, ..., x_n]\)换成\(f[x_0, x_1, ..., x_n，x_{n+1}]\)，也就是说我们需要\(n+2\)个点才能估计出均差形式的误差限。

第二种：差分形式的牛顿插值（牛顿前插公式）

同样的，我们可以通过构造差分表来获取\(x_0\)点处的各阶差分。

与均差形式的牛顿插值不同，差分形式的牛顿插值在解算误差限的时候只需要\(n+1\)个点。

不过我们依然可以看到，差分形式是由均差形式通过“均差-差分”（\(f[x_k, ..., x_{k+m}] = \frac{1}{m}\frac{1}{h^m}\Delta^mf_k，其中m=1,2,...,n\)）以及“差分-导数”（\(\Delta^nf_k = h^nf^{(n)}(\xi)\)，其中\(\xi \in [x_k, x_{k+n}]\)）这两层关系推出来的，也就是说将\(f[x, x_0, x_1, ..., x_n]\)换成了\(f^{(n+1)}(\xi)\)，这样就要求\(f(x)\)的\(n+1\)阶导数。

总结： 当插值函数是一个复杂函数（这里的复杂指的是原函数的导数不容易得出）时，如：\(f(x)=\sqrt{\frac{\cos x+2\sin x}{2\cos x-\sin x}}\)，想求\(n+1\)阶导数几乎是不存在的（除非你是徐半仙或者聂星人或者许外挂），这是我们就只能通过构造均差表来解算其误差限；当插值函数是一个简单函数时，如\(f(x)=\cos x\)，这时求\(n+1\)阶导数赶赶单单没有\(len\)何挑战，所以就可以构造差分表来解算误差限。

一般地，题目中应该会给我们\(n+2\)个点来研究\(n\)次的牛顿插值。但是如果题目中的原函数是复杂函数，并且只给了\(n+1\)个点，这个时候我们不用慌，还有\(PlanB\)——题目肯定是要我们求\(f(m)\)的近似值，其中\(m\in(x_0，x_n)\)，这个时候就相当于给了我们第\(n+2\)个点：\(m\)，我们就能够通过\(f(m)\)的值（代入表达式中获得的近似值）来求得\(f[x, x_0, x_1, ..., x_n]\)。

例题1（参考《数值分析 第五版》\(P_{32} 例题4\)）\(\Longrightarrow\) 均差形式的牛顿插值及其误差估计

题目： 给出\(f(x)\)的函数表求4次牛顿插值多项式，并由此计算\(f(0.596)\)的近似值及其误差限。

解答：

首先根据给定函数表构造《函数-均差表》：

所以我们可以得到：

所以有：\(f(0.596)\approx P_4(0.596)=0.63192\ 3237\)，另外我们有截断误差为：

\(PlanB\)：

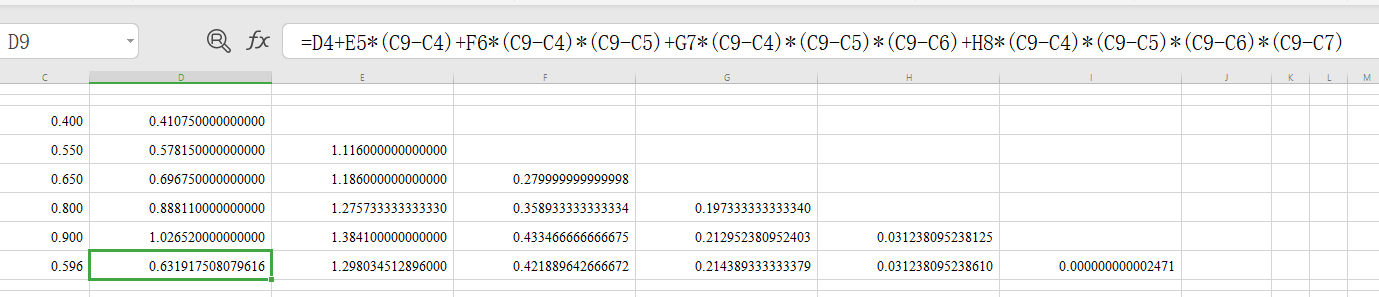
以下内容了解即可，考试时一般用不着！！！

大家不难发现，我这里保留了小数点后15位，那是不是保留10位或者更小的有效数字就为0了呢？我们不妨来看一下保留5位和7位的情况：

保留小数点后5位：

保留小数点后7位：

大家不难发现，结果并不是我们想象的那样简单，有效位数对误差影响是非常非常大的，正所谓“差之毫厘谬以千里”，但是我们不用慌，因为如图所示（天机就是拿来泄漏的🤪）：

所以大家就按部就班即可，题目还是很严谨的！！！

例题2（参考《数值分析 第五版》\(P_{34} 例题5\)）\(\Longrightarrow\) 差分形式的牛顿插值及其误差估计

题目： 给出\(f(x)=\cos x\)在\(x_k=kh\)（k=0,1,…,5\(、\)h=0.1\(）处的函数值，试用4次牛顿前插公式计算\)\(f(0.048)\)的近似值并估计误差。

解答：

首先构造差分表，并用牛顿前插公式：

由\(x=x_0+th\Longrightarrow t=\frac{x-x_0}{h}=0.48\)；所以有

其误差限函数为：

所以有：

总结：

均差表可以不用原函数求\(n+1\)阶导数，但是它的缺点就是难算，而且估计误差的时候需要\(n+2\)个点；

差分表的制作过程比均差表简单得多，而且可以不用第\(n+2\)个点就能估计出误差限，前提是原函数的导数必须是能求出来的；