循环群 |
您所在的位置:网站首页 › 构成半群的条件是什么 › 循环群 |
循环群
|
循环群
贡献者: 叶月2_ 本文存在未完成的内容。 循环群与自同构群的关系。 阿贝尔群是循环群的条件,相关定理应该拆分为新的一节。 需要大量实例,某些定理需要韦恩图说明。 定义 1若群 $G$ 的元素都是由某个元素生成,即 $G= \left\langle a \right\rangle $,则称群 $G$ 为循环群(cyclic group),称 $a$ 是循环群的生成元。 显然,循环群的群元都可以表示为生成元的整数次幂,因此循环群实际上是阿贝尔群。由群的封闭性可知,给定群 $G$ 的一个群元素 $g$,那么 $ \left\langle g \right\rangle \subset G$。 定义 2对于群 $G$,若 $H$ 是其循环子群,且不是其他循环子群的真子群,则称 $H$ 为 $G$ 的极大循环子群。 例 1整数群 $\mathbb Z$ 是有无限元素的循环群,群乘法为加法。 例 2模 $n$ 同余类 $\mathbb Z_n$。 例 3群 $G=\{-1,-\mathrm i,1,\mathrm i\}= \left\langle \mathrm i \right\rangle $。 循环群的形式看似没有什么规律,但我们可以借助同构来缩减研究对象。 定理 1无限循环群同构于整数加群;$n$ 元有限循环群同构于 $\{\mathbb Z_n;+\}$。 proof.1 设 $G$ 是无限循环群,建立 $\mathbb Z\rightarrow G$ 的同态映射,使得对于任意 $n\in \mathbb Z$,都有 $f(n)=a^n$。根据群同态基本定理习题 2 ,我们有 $\mathbb Z/ \operatorname {ker}f\cong G$。由于 $\mathbb Z$ 的正规子群都是 $n\mathbb Z,n\in \mathbb N$,因此模 $n$ 同余类与 $G$ 同构。当该 $n=0$ 时,对应无限循环群;当 $m\neq 0$ 时,$\mathbb Z_n$ 与 n 元循环群同构。 因为有限循环群可以继承整数群的乘法,因此还是一个环。可以证明,$\mathbb Z_n$ 环上的零因子是 $n$ 的因子。所以,如果 $n$ 是素数,那么这个环就是无零因子交换幺环了,我们一般简称其为整环。 定理 2有限整环必是域。 只要证明任意环元都有逆在环内即可。 因为是有限整环,假设生成元为 $a$,则由封闭性知对于每个非零同余类都必有 $a^m=a^n,m\neq n$。设 $m n$,因为 $a^{m-n}a^n=1\cdot a^n$,所以 $a^{m-n}=1$2。因此,$a^{m-n-1}$ 为 $a$ 的逆元,$a^{k(m-n-1)}$ 是 $a^k$ 的逆元,证毕。 习题 1无限循环群的生成元只有两个。 习题 2若 $n$ 元有限循环群 $G= \left\langle a \right\rangle $,那任意元素 $a^k,k\in N$ 的阶是多少。一个推论是:若 $k$ 与 $n$ 互素,则 $ \left\langle a \right\rangle = \left\langle a^k \right\rangle $,因此我们可以得知一个 $n$ 元循环群的生成元个数。 1. 循环群的子群结构 定理 3循环群的子群必是循环群。 proof. 设循环群 $G= \left\langle a \right\rangle $,则其子群元素必定包含 $a$ 的某次幂。设任意子群为 $G_1$ 包含元素的最小次幂为 $k$,则该子群包含 $a^{kn},n\in \mathbb Z$。若该群不是循环群,必然包含元素形如 $a^{kn+r}$,其中 $0 定理 4设 $G$ 是 $n$ 元循环群,若 $d|n$,则 $G$ 内存在唯一一个 $d$ 阶子群。 proof. 因为 $a^{\frac{n}{d}d}=e$,因此 $ \left\langle a \right\rangle ^{\frac{n}{d}}$ 是一个 $d$ 阶子群。下面证明唯一性。 设 $H=\{x\in G|x^d=e\}$,易证这是 $G$ 的子群且具有唯一性。又设 $x=a^k$,则 $a^{kd}=e$ 意味着 $n|kd$,则 $\frac{n}{d}|k$。因为 $G$ 是 $n$ 阶子群,所以 $k$ 的可能取值范围为 $\{1,2...n\}$,也即 $\{\frac{n}{d},2\frac{n}{d}...d\frac{n}{d}\}$。所以 $H$ 的阶小于或等于 $d$。 又因为 $a^{\frac{n}{d}}\in H$,则 $ \left\langle a \right\rangle ^{\frac{n}{d}}\subset H$,所以 $H$ 的阶必等于 $d$ 且 $H= \left\langle a \right\rangle ^{\frac{n}{d}}$。 换句话说,循环群的不同子群阶数不同。实际上,其逆命题也是成立的。即 $G$ 是循环群 $\Longleftrightarrow G$ 的不同子群阶数不同。 定理 5若群 $G$ 的不同子群阶数不同,则 $G$ 是循环群。 proof.3 设 $H$ 为 $G$ 的任意子群,因为共轭子群的阶与原群相等,即对于任意 $g\in G$ 都有 $|gHg^{-1}|=|H|$,题设条件使得 $G$ 的任意子群都是正规子群——$H\lhd G$。设 $G'=G/H$ 且 $H_1$ 是 $G'$ 的任意子群,那么对于 $G$ 而言,$H_1$ 是运算封闭的左陪集之并,也就是说,$H_1$ 也是原群的子群,题设及 “任意子群都是正规子群” 在商群意义上得以继承。 因此,我们可以利用循环子群来构造商群列。从 $G$ 里选任意元素 $x_1$,构造商群 $G_1=G/ \left\langle x \right\rangle _1$,从 $G_1$ 中选任意元素 $x_2$,构造商群 $G_2=G_1/ \left\langle x \right\rangle _2$,以此类推—— \begin{equation} G>G_1>G_2>...>G_{s-1}>G_S=\{e\}~. \end{equation} 我们知道,根据拉格朗日定理,商群的基数必是原群基数的因子,因此商群列总是有限的,最后终结于平凡群。又因为该平凡群是 $G_{s-1}$ 商去循环群得到的,所以 $G_{s-1}$ 必是循环群。接下来我们只需要证明,对于 $G_{n}=G_{n-1}/ \left\langle x \right\rangle _n$,若满足 $G_{n}$ 为循环群,则 $G_{n-1}$ 也必是循环群即可。这其实是从商群列逆向推导出 $G$ 是循环群。 设 $r$ 是 $G_n$ 的生成元代表元素,即 $r \left\langle x \right\rangle _n$ 生成了这个循环群。设 $|G_{n}|=d$,则对于任意 $r_1,r_2\in r \left\langle x \right\rangle _n$ 都有 $r_1^d,r_2^d\in \left\langle x \right\rangle _n$。$r_1\rightarrow r_1^d$ 是从左陪集 $r \left\langle x \right\rangle _n$ 到正规子群 $ \left\langle x \right\rangle _n$ 的映射,下面证明这是一个双射。 设 $r_1\neq r_2$,且 $r_1^d=r_2^d$。在 $G_{n-1}$ 中,$ \left\langle r \right\rangle _1$ 和 $ \left\langle r \right\rangle _2$ 是两个阶数相同,但元素不同的子群,与题设矛盾。所以 $r_1\rightarrow r_1^d$ 是单射。又因为正规子群和陪集的基数相同,所以该映射既单又满。 因此在 $r \left\langle x \right\rangle _n$ 中存在唯一的 $a$ 使得 $a^d=x$,把陪集表示为 $a^i \left\langle a^d \right\rangle ,i=1,2...d$,则 $G_{n-1}$ 确实是一个循环群,证毕。 取 $d=5$,上述的 $G_{n-1}$ 及其陪集划分如下图所示。 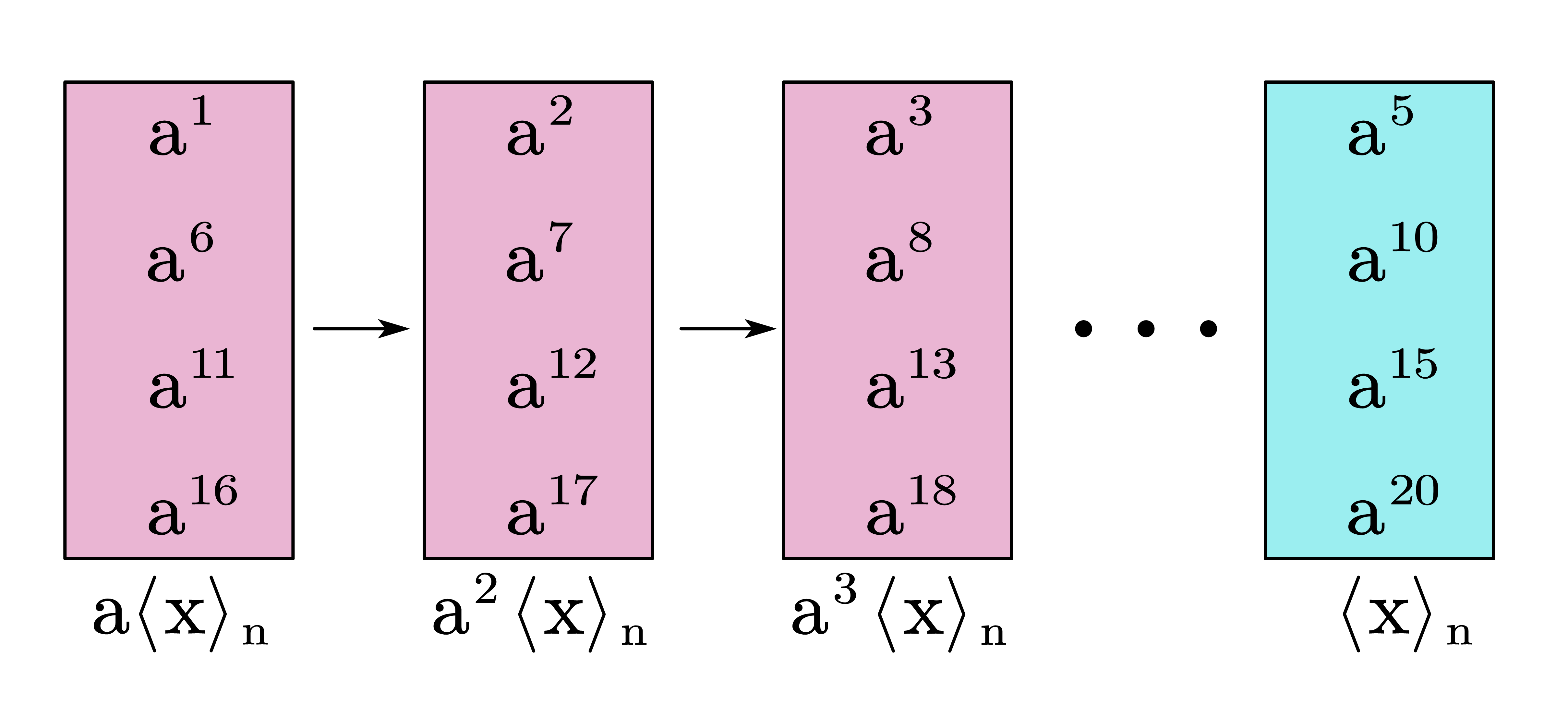 图 1:$G_{n-1}/x_n$
图 1:$G_{n-1}/x_n$
1. ^ 参考《抽象代数》,邓少强祝,朱富海著。 2. ^ 注意这是环上的乘法,由于乘法运算构成半群,消去律未必成立。若对于环上元素有 $ab=cb$ 且 $b\neq 0$,则 $(a-c)b=0$。由于整环没有零因子,所以 $a=c$,即消去律对整环必然成立。 3. ^ 引自《代数学基础》,Jier Peter 著。 致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。
友情链接: 超理论坛 | ©小时科技 保留一切权利 |
【本文地址】
今日新闻 |
推荐新闻 |