用python的scipy中的odeint来解常微分方程中的一些细节问题（适用于小白） |
您所在的位置：网站首页 › 指引牌模版 › 用python的scipy中的odeint来解常微分方程中的一些细节问题（适用于小白） |
用python的scipy中的odeint来解常微分方程中的一些细节问题（适用于小白）
|
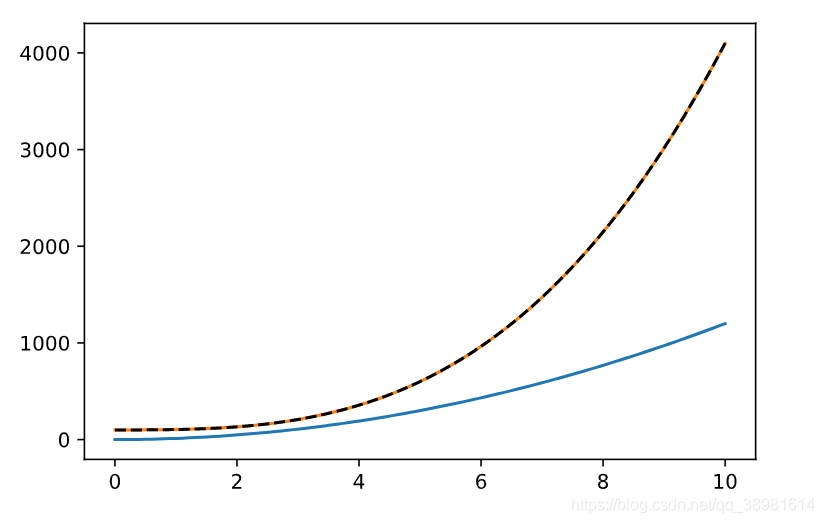
用python的scipy中的odeint来解常微分方程中的一些细节问题（适用于小白） 写在前面最近有些需要解决常微分方程的问题，网上查了很多教程都不是很明晰，便自己研究了一段时间，写一点小白初次接触这个方法应该如何理解，有哪些需要注意的点。 odeint在官网的参数很多，如下所示： scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)我们这次简单点只使用前三个参数scipy.integrate.odeint(func, y0, t)，如果想了解更多，其他教程应该有更详细的教学，这里只说一点最简单的原理和注意事项。 第一个参数是我们自行定义的需要求解的微分方程的函数第二个参数代表求解的微分方程的初值，没有初值微分方程的解不能唯一确定第三个参数是求解的微分方程中的自变量，应该是一个连续的序列值我们必须明确，求解微分方程最终我们得到的是一个关于自变量的函数，而不是一个值。 在此我们说一点基础的数学知识点，对于一个函数，比如 y = 4 x 3 + 100 y=4x^3+100 y=4x3+100 我们对它求导得到： y ′ = 12 x 2 y'=12x^2 y′=12x2 那么对应的，求解第二个微分方程就能得到第一个方程吗？ 答案是否定的，因为对第二个导数式子积分，得到的是： y = 4 x 3 + a ( 常 数 ) y = 4x^3 + a(常数) y=4x3+a(常数) 只有求解出常数a，才能唯一确定一个微分方程的解；否则我们得到的是一系列相差常数的解 官网例子说明在odeint的官网里面有个具体的例子，我们拿出来讲一讲， θ ′ ′ ( t ) + b ∗ θ ′ ( t ) + c ∗ s i n ( θ ( t ) ) = 0 \theta''(t) + b*\theta'(t) + c*sin(\theta(t)) = 0 θ′′(t)+b∗θ′(t)+c∗sin(θ(t))=0 官网的办法是说把这个二阶的微分方程先变换作一阶的方程组： θ ′ ( t ) = ω ( t ) \theta'(t) = \omega(t) θ′(t)=ω(t) ω ′ ( t ) = − b ∗ ω ( t ) − c ∗ s i n ( θ ( t ) ) \omega'(t) = -b*\omega(t) - c*sin(\theta(t)) ω′(t)=−b∗ω(t)−c∗sin(θ(t)) 这里边有一个代换过程： 令 ω ( t ) = θ ′ ( t ) \omega(t) = \theta'(t) ω(t)=θ′(t) 因此有： ω ′ ( t ) = θ ′ ′ ( t ) = − b ∗ ω ( t ) − c ∗ s i n ( θ ( t ) ) \omega'(t)= \theta''(t) = -b*\omega(t) - c*sin(\theta(t)) ω′(t)=θ′′(t)=−b∗ω(t)−c∗sin(θ(t)) 最终我们需要的两个方程是： θ ′ ( t ) = ω ( t ) \theta'(t)=\omega(t) θ′(t)=ω(t) ω ′ ( t ) = − b ∗ ω ( t ) − c ∗ s i n ( θ ( t ) ) \omega'(t)= -b*\omega(t) - c*sin(\theta(t)) ω′(t)=−b∗ω(t)−c∗sin(θ(t)) 随后官网根据这个代换过程定义了一个函数: def pend(y, t, b, c): theta, omega = y dydt = [omega, -b*omega - c*np.sin(theta)] return dydt或许有些python基础不是很好的同学对于这个函数比较陌生，我先来解释下， 参数b,c是系统的常数我们暂且承认即可t是微分方程的自变量，这个没有争议theta, omega = y，这句可能会有疑惑，我们传入的y到底是个啥？还记得前面的一阶代换过程嘛，简单来说就是把y先分成theta和omega，一个代表原微分方程theta第二个代表theta的一阶导；再对这两个求导就分别得到了一阶导和二阶导。 此函数返回的dydt是一个列表，分别代表theta的一阶导 和 二阶导 ，但是两阶导数是通过中间变量omega的一阶导数来表示的。这里面牵扯了一些数学代换，最终的式子为了变量减少，只能出现不带导数的theta和omega，看不懂先看下去，后面会有一个简单的例子来说明，我们先大概了解官网这个例子在说什么即可。 有些同学或许觉得现在我们就可以调用方程求解了，其实认真看的同学知道，我们此时还缺少关键的初始条件，否则无法确定唯一的一个解。为了方便此时我们把系统变量b，c同时定义好： b = 0.25 c = 5.0 y0 = [np.pi - 0.1, 0.0] #初始条件此处初始条件有两个是因为，我们有一个方程组（两个方程），原方程和一阶方程都需要初始条件（同样可以看到后面的简单例子）。 在编程时我们还需要定义自变量，这个也很重要， t = np.linspace(0, 10, 101)到此为止，准备工作全部完成，我们可以求解了。 sol = odeint(pend, y0, t, args=(b, c))其实我们会发现这个结果sol，是一个形状为(101，2)的数组。第一列是theta(t)，第二列是omega(t),也就是说得到了两个解，theta(t)是原微分方程的解，omega(t)是原方程的一阶导数方程。 plt.plot(t, sol[:, 0], 'b', label='theta(t)') plt.plot(t, sol[:, 1], 'g', label='omega(t)') plt.legend(loc='best') plt.xlabel('t') plt.grid() plt.show()通过调用以上语句，官网分别画出了结果的图像，如下所示， 这是我看完的几个疑问，如果你愿意跟我一起，通过下面的代码进行测试，我相信，你会对这个odeint有更深一点的理解。 测试 1先定义好数学问题就拿我们前面举过的例子来说吧，对于下面的函数【1】， y = 4 x 3 + 100 y=4x^3+100 y=4x3+100 我们对它求导得到表达式【2】： y ′ = 12 x 2 y'=12x^2 y′=12x2 这是一个一阶微分方程，表达式【1】是它的一个解（别忘记常数） 我们在此求导得到表达式【3】， y ′ ′ = 24 x y'' = 24x y′′=24x 这是一个二阶微分方程，表达式【1】是它的一个解（同样别忘记常数） 先求一阶的结果如果我们想求表达式【2】y’=12x^2 在初值为100（本文指的是x=0时）的情况下，这个微分方程的解是多少，我们编写如下函数， initial = 100 # 定义原方程初始值 def f1(y,x): return 12*x**2 x = np.linspace(0,10,100) #定义自变量 result1 = odeint(f1,initial,x) #调用求解 plt.plot(x,result1) #求解值 plt.plot(x,4*x**3+initial,'--k') #真实值这里我们会发现我们需要定义的微分方程函数，返回的都是某个变量的一阶导数，所以说这个odeint在调用时填入的参数fun句柄，应该是以一阶微分形式给出的，所以以后定义这种函数我们应该都化为一阶然后写好自定义函数，再传入odeint里面。 本文初值为100，指的是x=0时，y=100。请思考如果是x=1时，y=104该如何表示！
上图结果说明一阶的求解结果完全正确。 二阶微分方程的测试如果我们想求解表达式【3】y’’ = 24x 在初始值100 和 一阶初值 0 的情况下的解， 此时应先化为一阶方程组，令 ω = y ′ \omega = y' ω=y′ y ′ ′ = ω ′ = 24 x y'' = \omega' =24x y′′=ω′=24x 确认如下结果方程组： y ′ = ω y' = \omega y′=ω ω ′ = 24 x \omega' =24x ω′=24x 如此保证方程左边是一阶组，右边是不含导数项。 我们应该编写如下函数， initial = 100 #原初值 derivative1 = 0 #一阶初值 def f2(y,x): y1,w = y return np.array([w,24*x]) #返回值列阵 先一阶 再 二阶 由低到高 x = np.linspace(0,10,100) #定义自变量 result2 = odeint(f2,(initial,derivative1),x) #初值对应 先原方程 再 一阶 由低到高 plt.plot(x,result2) plt.plot(x,4*x**3+initial,'--k')
如果我们调换一下初值的顺序(initial,derivative1)为(derivative1，initial)，即先一阶导再二阶导，会发生什么呢？结果还正确嘛？ initial = 100 derivative1 = 0 def f2(y,x): y1,w = y return np.array([w,24*x]) x = np.linspace(0,10,100) #result2 = odeint(f2,(initial,derivative1),x) #初值对应 先原方程 再 一阶 由低到高 【注释掉】 result2 = odeint(f2,(derivative1,initial),x) #初值对应 先一阶 再 原方程 会出现错误【如下图】 plt.plot(x,result2) plt.plot(x,4*x**3+initial,'--k')
可以看出来，如果改变初值顺序结果是错误的。那么这个顺序应该跟谁对应呢？ 那尝试如果改变初值顺序改变的情况下，把自定义函数的返回值也调换，会不会得到正确结果呢？ 我们看下面的代码： def f2(y,x): y1,w = y # return np.array([w,24*x]) #返回值列阵 先一阶 再 二阶 由低到高 【注释掉】 return np.array(24*x,w) #返回值列阵 先 二阶 再 一阶 由高到低 x = np.linspace(0,10,100) result2 = odeint(f2,(derivative1,initial),x) #初值对应 先一阶 再 原方程 会出现错误 plt.plot(x,result2) plt.plot(x,4*x**3+initial,'--k')结果会报错： RuntimeError: The size of the array returned by func (1) does not match the size of y0 (2).这是因为在自定义函数中y1,w = y应该和返回值对应，如此应该调换为w,y1 = y def f2(y,x): # y1,w = y #【注释掉】 w,y1 = y # return np.array([w,24*x]) #返回值列阵 先一阶 再 二阶 由低到高 【注释掉】 return np.array([24*x,w]) #返回值列阵 先 二阶 再 一阶 由高到低 x = np.linspace(0,10,100) result2 = odeint(f2,(derivative1,initial),x) #初值对应 先一阶 再 原方程 会出现错误的结果 plt.plot(x,result2) plt.plot(x,4*x**3+initial,'--k')
这样我们得到了正确的结果 总结这么麻烦，我们其实只说明了一个很简单的问题，初始值、返回值、中间变量这 三个位置的顺序必须完全相同， 正序或者逆序 都可以，但三个必须保持一致，才能出现正确的结果。 这个顺序我的理解是 原方程-一阶导-二阶导 这样的顺序。 初始值对应的 以及 返回值和中间变量替换对应的 应该是同样的次序， 比如 如果返回值列表是[一阶导 二阶导] 那么初始值对应的应该为[原方程初值 一阶导初值]，变量替换对应的元组也应该同一阶导和二阶导对应。 这是关于这个函数的第一篇，我也是刚接触这个东西第二天，不确定以后会不会继续写，希望不会误人子弟吧。有些地方表述可能不清楚，以后会修改。欢迎批评指正，另外不要杠我，你杠就是你对。 |
官网的介绍到此为止了，我不知道有没有小伙伴看完和我一样很懵，定义微分方程为什么是这样的，还有没有别的可能，关于这个odeint有没有别的需要注意的点，这一个例子感觉说的不那么明白，比如我有以下疑问：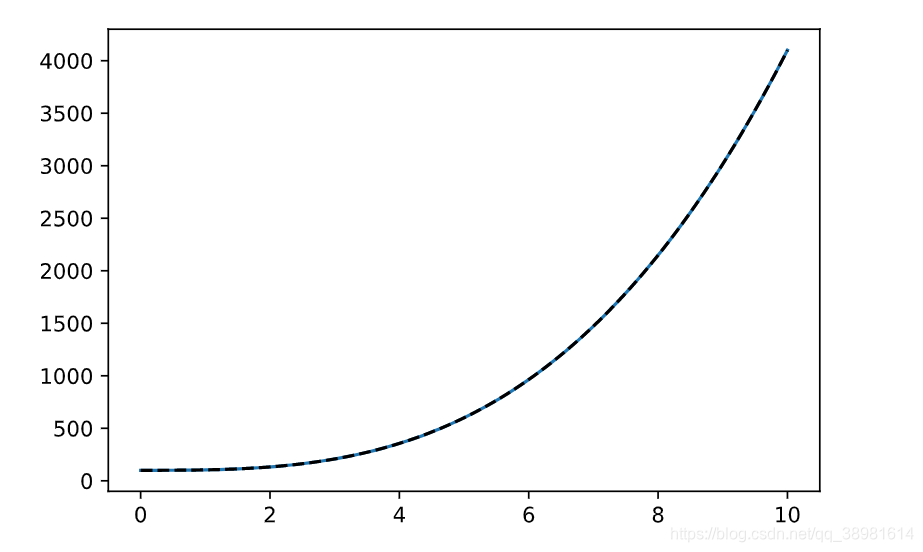
可以发现原方程的结果是吻合的。
【本文地址】