第五章 关系 |
您所在的位置:网站首页 › 并交运算法则 › 第五章 关系 |
第五章 关系
|
文章目录
前提知识什么是二元关系二元关系定义二元关系的数学符号枚举二元关系
空关系 &全域关系& 恒等关系定义域和值域关系的性质(1)自反性与反自反性(2)对称性与反对称性(3)传递性关系的性质矩图证明自反性与对称性与传递性
关系的表示枚举法&叙述法表示例子关系的图形表示关系矩阵方式
关系的运算(1) 布尔矩阵的并和交运算(2)关系矩阵的布尔运算(3)关系的并交差补运算(4)关系的复合运算定义复合运算的关系图法/关系矩阵总结 (关系的复合运算)关系的复合运算公式1.结合律2.分配律
(5)关系复合逆运算定义(6)关系的逆运算定理逆运算公式
(7)关系的幂运算幂的性质
关系的闭包关系闭包的公式
等价关系与序关系前提
等价关系与商集
前提知识
整除关系需满足 除数,被除数,商都是整数 (0,-3也属于整数) A整除B(A/B)=商(), 余数是0 ,而A是被除数,B是除数 小于等于关系LA ,整除关系DA 什么是二元关系
令A为某大学所有学生的集合,B表示该大学开设的所有课程的集合,则AxB可表示该校学生选课的所有可能情况.而真正的选课情况则会是AxB的某一个子集 令F为某地所有父亲的集合,S表示该地所有儿子的集合,则FXS可表示父子关系的所有可能情况,而真正的父子关系则会是FxS的某一个子集
二元关系定义
设A,B为两个非空集合,称AxB的任意子集R为从A到B的一个二元关系,简称关系 其中 A称为关系R的前域 , B称关系R的后域 ,如果A=B,则称R为A上的一个二元关系 二元关系的数学符号 若有序对/序偶∈R, 通常把这一切事实记作xRy , 读作"x对y有关系R" 反之X对y没有关系R
枚举二元关系 幂集: 集合内的若有n个元素,则排列0元子集,一元子集,二元子集…n元子集 而二元关系是笛卡尔积的子集,若要求求出所有的二元关系,则需要先求出笛卡尔积,再进行幂集排序
空关系 &全域关系& 恒等关系
EA ={|x∈A ∩ y∈B}= A x A IA= { |x∈A } 举例 集合 A={1,2} EA=AxA ={,,,} IA={,} 定义域和值域
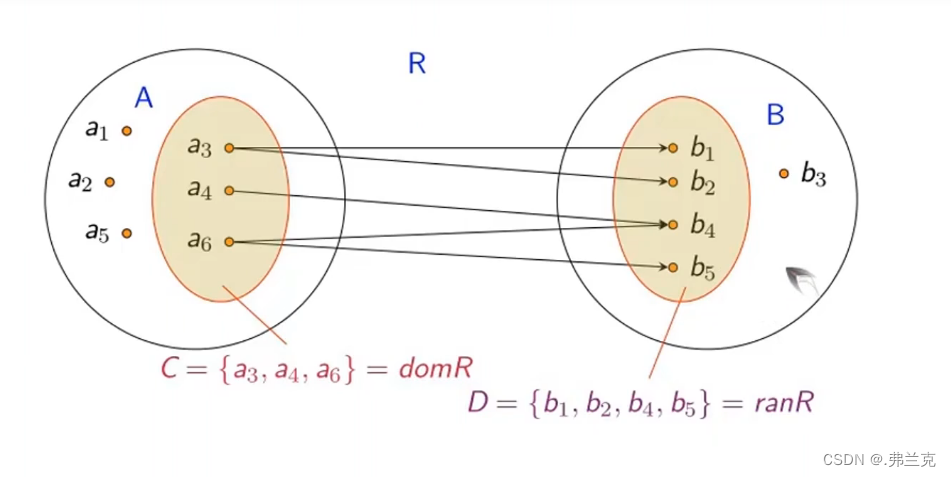
设R是从A到B的二元关系, 则A为关系R的前域, B为关系R的后域. 令C={x|x∈A, ∃y∈B, ∈R}, D={y|y∈B, ∃x∈A , ∈R} 称C为R的定义域,记作C=domR , D为R的值域, 记作D=ranR R的域: fldR(域)= (定域U值域) domR U ranR
例子 比如X={1,2,3},在X上有关系R={, < 3,2>} 则定义域domR 是{1,3} [ 定义域是将每个关系的第一元素拿出来] 则值域ranR是{1,2} [ 值域是将每个关系的第二元素拿出来] 而域fldR是{1,2,3} 关系的性质 (1)自反性与反自反性 设R为A上的关系 (1)若∀x x∈A → ∈R,则称R在A上是自反的 可以理解成∀x,有xRx (2)若∀x x∈A → ∉R,则称R在A上是反自反的 可以理解成∀x,有x和x没有关系R 若R是自反的,则推出R不是反自反的; 若R是反自反的,则推出R不是自反的 自反关系: A上的全域关系EA, 恒等关系IA ,小于等于关系LA,整除关系DA 反自反关系: 实数集上的小于关系,幂集上的真包含关系
举例 若A={1,2,3},R1,R2,R3是A上的关系,以下判断的自反性质 R1 = {,} , 是自反的,不是反自反的 因为左式代表不存在关系,则与是自反的关系,相违背。 则称R1不是自反的,又因不存在关系称为反自反的,则推导出R1也不是反自反的 R2 = {,,< 3,3>,},是自反的,不是反自反的 因为自反的关系都存在, R3= {} 不是自反的,是反自反的 ,因为不存在关系
(2)对称性与反对称性 设R为A上的关系 (1)若(∀)(∈R →∈R),则称R在A上是对称的 可以理解成 若 ∀有xRy 则 yRx (2)若(∀)(∈R 且∈R → x=y ),则称R在A上是反对称的 可以理解成 若 ∀有xRy且 yRx, 则x=y 对称关系: A上的全域关系EA , 恒等关系IA 和 空关系Ø 反对称关系: 恒等关系IA, 空关系Ø
举例 若A={1,2,3},R1,R2,R3是A上的关系,以下判断的对称性 R1 = {,} 是 对称的,是反对称的 因为左式,右式都是T,则称是对称的 ,同理也是对称的 因为左式,成立T,且1=1,则称是反对称的 ,同理也是反对称的 R2 = {,,}, 是对称的,不是反对称的 因为是对称的, 可以推导.则是对称的 因为是反对称的, 左式且成立T,但1≠2,则不是对称的 R3= {,} ,不是对称的,是反对称的 因为不能推导则T蕴含F,则不是对称的,同理也不是对称的 因为且不存在关系,则左式为F,则是反对称的,同理是反对称的 R4= {,,} 不是对称的,不是反对称的 (3)传递性
定义 设R为A上的关系,若(∀)(∀) (∈R ⋀ ∈R→ ∈R ),则称R是A上的传递关系 可以理解成 若 xRy 且yRz ,则xRz A上的全域关系EA ,恒等关系IA , 空关系Ø, 小于等于关系,小于关系,整除关系,包含关系,真包关系
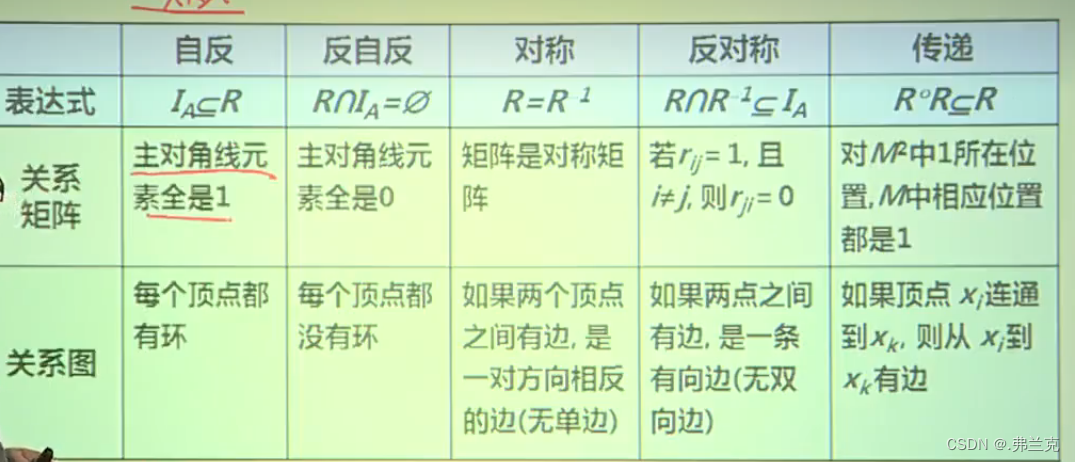
举例 若A={1,2,3},R1,R2,R3是A上的关系,以下判断的传递性 R1={,} 是传递的 R2={,} 不是传递的 因为不存在所以为F, T(且)蕴含F,则不是传递的 R3={} 是传递的 因为左式为F ,则是传递的 关系的性质矩图
关系的表示
关系是一个特殊的集合,因此集合的 两种基本表示法(枚举法和叙述法)可以用到关系的表示中 枚举法&叙述法表示例子
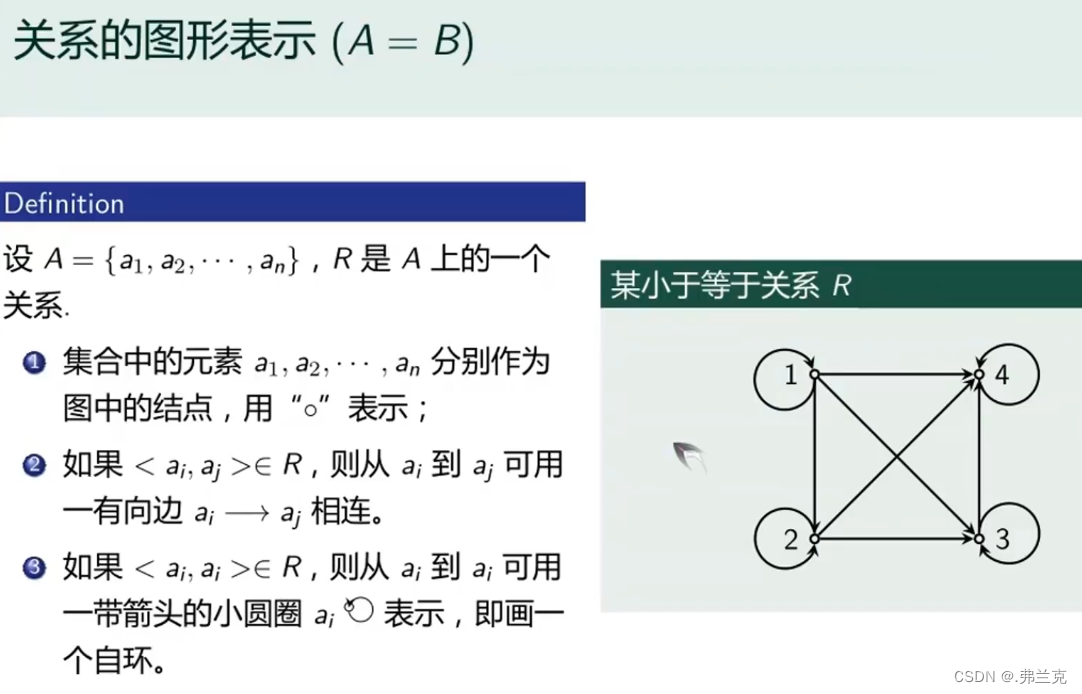
关系的图形表示
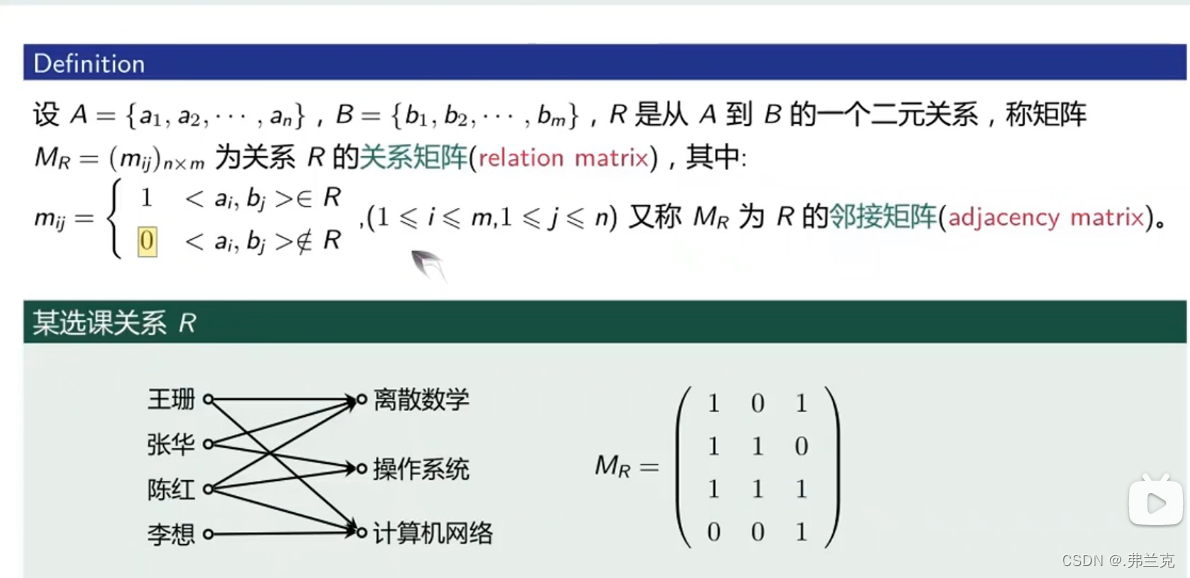
关系矩阵方式 关系矩阵内的1,0数学意义: 1表示A和B有关系;0表示A和B没关系 1代表A到B有关系R, 0代表A到B没有关系R
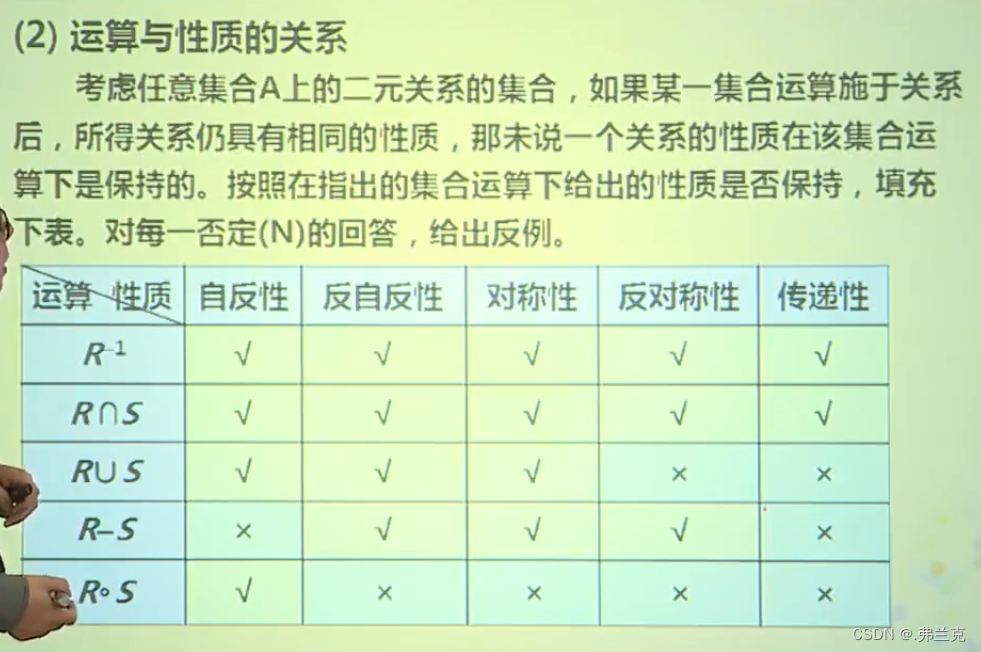
关系的运算 集合是父类,关系是子类 关系是一种特殊的集合,因此集合所有的基本运算(交,并,差,补) 都可以应用到关系中,并且同样满足集合的所有运算定理
(1) 布尔矩阵的并和交运算
(2)关系矩阵的布尔运算 理解: 最右边 A与B的积运算的第一排的第一列是1 ,求法是左边A第一排和B第一列中,若存在 1 1对应则,结果为1,否则为0 1 0 1 0 0 1 = 1
(3)关系的并交差补运算
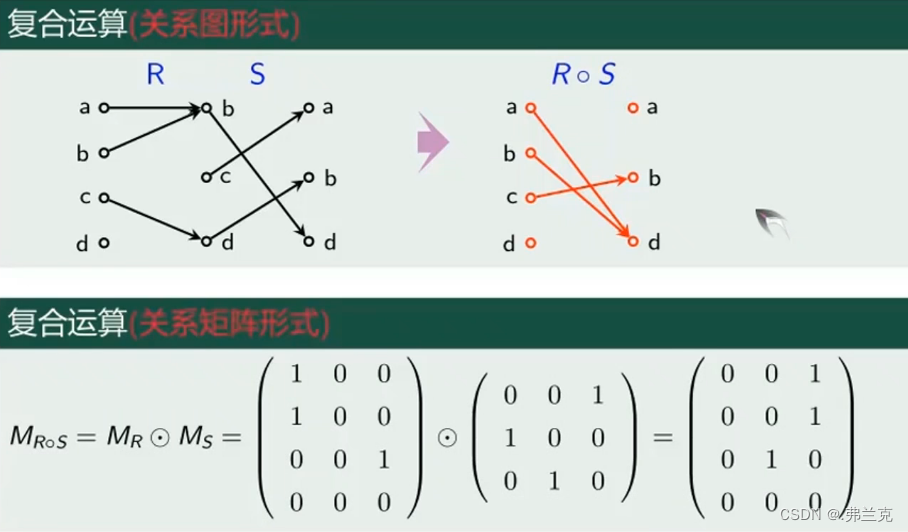
(4)关系的复合运算定义
复合运算的关系图法/关系矩阵
总结 (关系的复合运算)
注意: R∘ S ≠ S ∘ R (R∘ S) ∘ T = R ∘ (S ∘T) (F ∘ G) -1 = G -1 ∘ F -1 MR∘S = MR ⨀ MS 1.结合律
2.分配律
(5)关系复合逆运算定义
(6)关系的逆运算定理 I. R的关系图中,改变箭头方向即得R -1的关系图, II. R与R -1 的关系互为转置矩阵(就是行和列互换) III. R-1 的定义域和值域正好是R的值域和定义域 IIII. domR = ranR -1 , ranR = domR-1 |||||. |R|=|R -1| 逆运算公式定理 设R和S是集合A到B的二元关系,则⋃⋂ ⋁⊆ (1)MR⋂S = MR ⋀ MS (2)MR⋃S = MR ⋁ MS (3)若R⊆S,则R-1 ⊆ S-1 (4)若R⊆S,则Rc ⊆ Sc(c表示的是R的补集=EA-S=AxB-S) (5)(R ⋂ S)-1= R-1 ⋂ S-1 (6)(R ⋃ S)-1= R-1 ⋃ S-1 (7)(R ⋂ S)c= Rc ⋃ Sc (和德摩根定律类似 ~(A⋂B)= ~A ⋃ ~B ) (7)(R ⋃ S)c= Rc ⋂ Sc (和德摩根定律类似 ~(A⋃B)= ~A ⋂ ~B )
(7)关系的幂运算
幂的性质
幂运算的收敛性 定义设R是非空集合A上的关系,R的自反(对称/传递)闭包R1满足以下条件 1.增加条件后,自反闭包R1是自反的 2.关系R⊆自反闭包R1 3.对于A上包含R的自反关系R11 , 有R1⊆R11, 则将R的自反闭包记作 r(R),一般称R的自反闭包记作r( R), 对称闭包 记作 s( R) 传递闭包 记作 t( R) 或者称:自反闭包包含R的最小的自反关系,就叫做自反闭包 关系闭包的公式 1. r( R) = R⋃ IA 2. s( R) = R⋃ R-1 3. t( R) = R⋃ R2⋃ R3⋃ R4⋃ R5⋃ R6…⋃ Rn
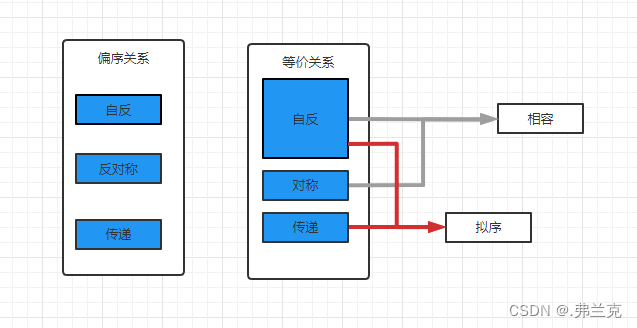
等价关系与序关系 前提 等价关系是特殊的二元关系序偶的集合 A上的关系R的等价关系构成的集合是集合A的子集
设A={1,2,3},确定A的所有划分 注:π是划分关系的集合 π1= { {1},{2},{3}} ,它的划分块是3 π2= { {1,2},{3}} , 它的划分块是2 π3= { {1},{2,3}} , 它的划分块是2 π4= { {1,3},{2}} , 它的划分块是2 π5={A} , 它的划分快是1 共有五种划分方式 等价关系与商集 定义1 设R为非空集合上的关系,若R是自反的,对称的,传递的,则称R为A上的等价关系. 设R是一个等价关系,若∈R,称x等价于y 记作x~y 定义2 设R为非空集合A上的等价关系,令x∈R,[x]R= {y|y∈A ⋀ xRy },称[x]R为x关于R的等价类,简称为x的等价类,简记为[x] 理解来说: 在等价关系R下,与x的有关系的其他元素,包括他自己,构成的一个集合,就叫做x的等价类 定理 设R设非空集合A上的等价关系,则 (1)∀ x ∈ A ,[x]是A的非空子集. (2)∀x,y∈A,如果xRy,[x]=[y] (3)∀x,y∈A,如果x和y没有关系R,则[x]≠[y] U{ [x]| x∈A} = A,即所有等价类的并集就是集合A 商集的定义 设R为非空集合A上的等价关系,以R的所有等价类作为元素的集合称为R的商集S,记作A/R A/R ={ [ [x]R | x∈A } 比如集合A={1,2,3,4,5,6,7,8},x和y取余3相等的等价关系R={,,,,,,,,.,,,,,,,,< 3,3>,< 3,6>,} A/R = { [1]R , [2]R , [3]R } 举例1 A mod B = A取余B
举例2 设X= {1,2,3,4},X的划分S={ {1} , {2,3} , {4} },试写出S导出的等价关系R R={ , ,,< 3,2>,< 3,3>, }
|
【本文地址】
今日新闻 |
推荐新闻 |























 因为 I A o R = R = I B o R, R0+1 =R0 +R1 ,得R0= I A
因为 I A o R = R = I B o R, R0+1 =R0 +R1 ,得R0= I A






 举例
举例 [1]=[4]=[7]={1,4,7} ,表示 1mod 3 = 4mod3 = 7mod 3 ,余数都是1 [2]=[5]=[8]={2,5,8} 2mod 3 = 5mod3 = 8mod 3 ,余数都是2 [3]=[6] 3mod3 = 6 mod 3,余数都是0
[1]=[4]=[7]={1,4,7} ,表示 1mod 3 = 4mod3 = 7mod 3 ,余数都是1 [2]=[5]=[8]={2,5,8} 2mod 3 = 5mod3 = 8mod 3 ,余数都是2 [3]=[6] 3mod3 = 6 mod 3,余数都是0