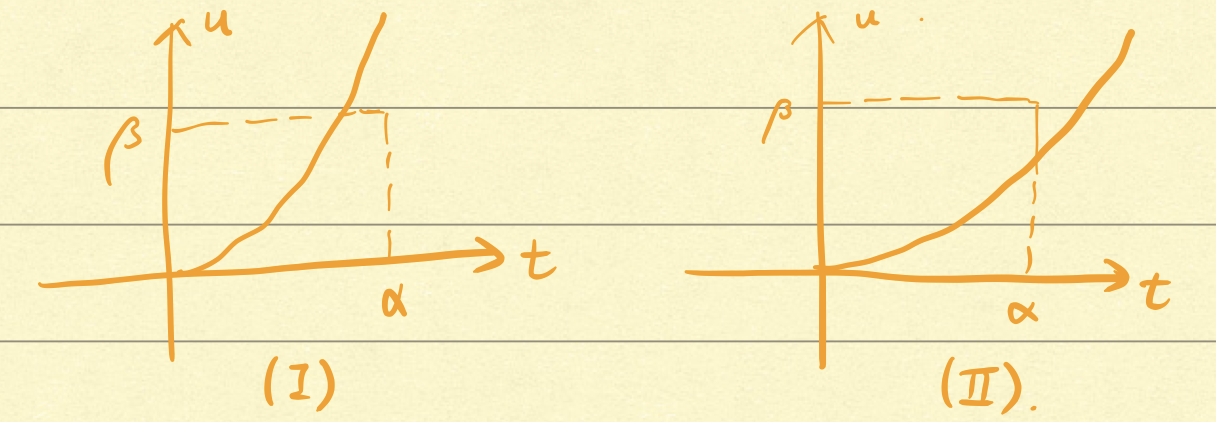这一章节研究度量空间的基本结构，在开始前，我们需要思考几个问题：

在这篇笔记的最后再来回答这个问题。

对于工科生来说，“空间”这个概念还是比较模糊的，但是我本人在学习数学的过程中发现很多数学的分支学科都是对于某个空间进行研究，比如欧氏空间、内积空间、测度空间、拓扑空间、希尔伯特空间，以及这门课要学习的度量空间等等。

个人觉得，定义空间的同时往往伴随着相应的某种运算的定义，也就是说我们研究空间的时候，主要还是为了研究某些运算，为了保证运算前后的结果都有比较好的性质（或者说便于处理），我们才抽象出了对应的空间的概念。回到这门课，泛函分析里面将要遇到的空间都是度量空间，因此我们首先需要知道他的定义。

“度量”实际上指的就是抽象的“距离”，比如两个点的距离、两个向量的距离、两个无穷长序列的距离、两个连续函数的距离。尽管点、向量、无穷长序列、连续函数的形式差别很大，但是如果我们都把他们抽象成为高维空间中的一个点，我们可以用相似的方式定义距离（也就是度量）的概念。

这样一来，由于大多数时候我们关心的是两个高维点之间的相对距离，而不是他们本身的绝对坐标（比如我们研究数列收敛性 \(x_n\to x\) 的时候，只需要分析 \(|x_n-x|\to 0\) 是否成立，而不太关心 \(x\) 具体是什么），因此抽象出距离这个概念之后，我们就可以把点、向量、序列、连续函数都统一的看待，用统一的方法和理论处理相似的问题。

首先，我们可以抽象出一个集合 \(X\)。\(X\) 可以是一个实数点集，比如 \(X=\mathbb{R}\)；也可以是一个多维实空间 \(X=\mathbb{R}^n\)，他的元素就是向量；也可以是连续函数集 \(X=C[a,b]\)，表示区间 \([a,b]\) 上的所有连续函数构成的集合。

现在问题的关键就是如何定义度量？当然不能随意定义，我们必须要他满足一定条件，才能称之为度量：

根据定义可以看出来，度量就是一种距离，称 \((X,d)\) 为度量空间（或距离空间）。下面给出一些度量空间的例子，要证明是否是度量只需要验证几条定义即可。

注：后面的内容基本都默认我们是在度量空间 \((X,d)\) 中讨论，为了书写省劲，一般都没有明确写出来“存在度量空间 \((X,d)\)”，但是需要注意我们是在度量空间中讨论的。

例子 1(离散度量)：定义 \[ d(x,y) = \begin{cases} 0, & x=y \\ 1, & x\ne y \end{cases} \] 例子 2：记 \(X=\mathbb{K}\)，其中我们记 \(\mathbb{K}=\mathbb{R} \text{ or } \mathbb{C}\)（后面的笔记也都保持这个习惯），\(d(x,y)=|x-y|\)，那么 \((X,d)\) 是一个度量空间。

例子 3：\(X=\mathbb{K}^n, d_p(\boldsymbol{x,y})=\|\boldsymbol{x-y}\|_p = (\sum_i |x_i-y_i|^p)^{1/p}\)，对于 \(1\le p \le \infty\)，\((X,d_p)\) 是度量空间。

例子 4：\(X=\ell^p,d_p(\boldsymbol{x,y})=\|\boldsymbol{x-y}\|_p\)，对于 \(1\le p\le \infty\)，\((\ell^p,d_p)\) 是度量空间。其中 \[ \ell^p = \left\{(x_n)_{n\ge1},\ x_n\in\mathbb{K},\ \exists c\ge0,\ |x_n|\le c \right\} \] 这个在证明的过程中需要证明 \(\forall x,y\in\ell^p\)，都有 \(x+y \in \ell^p\)。

例子3、4的证明过程中还需要用到两个比较重要的不等式：Hölder 不等式和 Minkowski 不等式。

Hölder不等式：\(\forall 1\le p,q\le\infty, \frac{1}{p}+\frac{1}{q}=1,\forall x,y\in\mathbb{R}^n\)，有 \[ \sum_{i=1}^{n}|x_iy_i| \le \|x\|_p \|y\|_q \] 当 \(p=q=2\) 的时候，上面的式子就退化成 Cauchy-Schwarz 不等式。

证明：可以取 \(u(t)=t^{p-1},t\ge0\)，反函数就有 \(t=u^{\frac{1}{p-1}}=u^{q-1},u\ge0\)。考虑可能有下面两种情况：

以第一种情况为例，\(\int_0^\alpha t^{p-1}dt + \int_0^\beta u^{q-1}du = \frac{\alpha^p}{p}+\frac{\beta^q}{q} \ge \alpha\beta\)，第二种情况也有相同的结果。我们可以首先假设 \(\|x\|_p = \|y\|_q=1\)，因而就有 \[ |x_iy_i| \le \frac{|x_i|^p}{p} + \frac{|y_i|^q}{q} \\ \Longrightarrow \sum |x_iy_i| \le 1 = \|x\|_p \|y\|_q \] 如果 \(\|x\|_p \ne 1\)，那么我们可以取 \(x' = x/\|x\|_p\)，代入上面的情况就能得到 Hölder 不等式了。证毕。

Minkowski 不等式：\(\forall x,y\in\ell^p, p\ge1\)，都有 \[ \|x+y\|_p \le \|x\|_p + \|y\|_p . \] 证明：

证毕。

对于空间 \(\ell^p\) 还有如下有趣的性质：

例子 5(无穷维向量)：定义 \(S=\{(x_n)_{n\ge1}, x_n\in\mathbb{K}\}\)，定义如下度量 \[ d(x,y) = \sum_{n=1}^\infty\frac{1}{2^n}\frac{|x_n-y_n|}{1+|x_n-y_n|} < \infty \] 则 \((S,d)\) 是度量空间。

例子 6(连续函数)：\(X=C[a,b],\ d_p(x,y) = \left(\int_a^b |x(t)-y(t)|^pdt\right)^{1/p},\ 1\le p\le\infty\)，则 \((X,d)\) 是度量空间。

上面一小节分析了度量空间 \((X,d)\) 中度量 \(d\) 的定义，这一部分研究一下集合 \(X\) 的性质。我们主要从开集和闭集这个角度来分析集合的结构。

需要注意的是在实空间 \(\mathbb{R}\) 当中我们对开集（开区间）都比较熟悉了，但是还有很多其他很复杂的集合，比如上面提到的连续函数构成的集合 \(C[a,b]\)，这种情况下什么是开集呢？这个时候我们就需要抽象出“开集”这个概念最为本质的性质了。

定义：开球 \(B(x_0,\delta)=\{x\in X,\ d(x,x_0)0, B(x_0,\delta)\subset M\)，\(M\) 的所有内点的集合称为 \(M\) 的内部，记为 \(\mathring{M}\)。

定义：\(M\) 为开集 \(\iff M=\mathring{M} \iff \forall x\in M,\ \exists \delta>0,\ B(x,\delta)\subset M\)。

定义：\(F\subset X\) 为闭集 \(\iff F^c=X\setminus F\) 为开集。

定义：闭包 \(\bar{M}=\{x\in X,\ \forall \delta>0,\ B(x,\delta)\cap M\ne \varnothing \}.\)

注 1：有的集合可能既不是开集，也不是闭集！比如实空间 \(\mathbb{R}\) 中区间 \([0,1)\)。

注 2：但是假如现在考虑的不是实空间，而是 \(X=[0,+\infty)\)，那么 \([0,1)\) 就是开集！判断是否是开集还是要根据定义！

例子 1(离散度量空间)：\((X,d)\) 为离散度量空间，那么任意的 \(M\subset X\) 都是既开又闭的集合。因为我们可以取 \(\forall x\in M,\ B(x,1/2)=\{x\}\subset M\)。

命题：\(\mathring{M}\) 为包含在 \(M\) 中的最大开集。

证明：分为三个过程：1）\(\mathring{M}\subset M\)；2）\(\mathring{M}\) 为开集；3）\(\mathring{M}\) 最大。注意不要忘了第 2) 部分，细节略。

定理：\((X,d)\)，则

证明：略。

定理：\((X,d)\)，则

证明：略。

性质：闭包 \(\bar{M}\) 为闭集，且 \(\bar{M}\) 为包含 \(M\) 的最小闭集。

推论：\((X,d), M\subset X\)，\(M\) 为闭集 \(\iff M=\bar{M}.\)

证明：略。

拓扑空间

拓扑的定义是：给集合 \(X\) 指定拓扑，就是指定集合 \(X\) 中哪些子集是开集，指定的方式需要满足：

\(X\) 上的拓扑 \(\mathcal{T}\) 是 \(X\) 的子集族，满足上述的条件。定义了拓扑 \(\mathcal{T}\) 的集合 \(X\) 称为拓扑空间。对于拓扑空间 \((X,\mathcal{T})\) 有子集 \(\mathcal{O}\)，若 \(\mathcal{O}\in \mathcal{T}\)，则称 \(\mathcal{O}\) 为开集。

注1：先有拓扑 \(\mathcal{T}\)，然后如果 \(X\) 的子集 \(\mathcal{O}\in \mathcal{T}\)，才有 \(\mathcal{O}\) 是开集的说法。

注2：拓扑空间跟度量空间类似，首先定义了一种运算，比如度量空间是需要定义度量，拓扑空间是需要定义对开集封闭的运算（有限交、任意并），其中的元素对这些运算封闭，然后才有空间的概念.

定义：称 \(M\subset X\) 是 \(X\) 的稠密子集，若 \(\bar{M}=X\)。换一种表述方式，也就是说 \(\forall x\in X,\forall \delta > 0, B(x,\delta)\cap M\ne \varnothing\)。

例子 1：\((\mathbb{R},d)\)，其中 \(d(x,y)=|x-y|\)，则 \(\bar{\mathbb{Q}}=\mathbb{R}.\)

例子 2：\((\mathbb{C},d)\)，其中 \(d(x,y)=|x-y|\)，则 \(\overline{\mathbb{Q}+i\mathbb{Q}}=\mathbb{C}.\)

例子 3：\((\mathbb{R}^n,d_2)\)，则 \(\overline{\mathbb{Q}^n}=\mathbb{R}^n.\)

例子 4：对于 \(1\le p\le \infty\)，定义 \(M=\{(x_n)_{n\ge1},\ x_n\in\mathbb{Q},\exists N,\forall n\ge N, x_n=0 \}\)，那么对于度量 \(d_p\)，有 \(\bar{M}=\ell^p.\)

性质：对于两个度量 \(d_1,d_2\)，如果存在 \(c_1,c_2>0\)，对 \(\forall x,y\in X\)，都有 \(c_1d_1(x,y)\le d_2(x,y)\le c_2 d_1(x,y)\)，也即这两个度量相互控制，那么对任意 \(M\subset X\)，有 \(M\) 的闭包相同，内部也相同。

例子 5：对于离散度量空间，\(X\) 的稠密子集只有 \(X\) 本身。

例子 6：\(X=C[a,b]\)，\(d_\infty(x,y)=\max_{t\in[a,b]} |x(t)-y(t)|\)，因此 \(M=\{多项式 p(t)=a_0+a_1t+\cdots+a_Nt^N,a_i\in\mathbb{Q}\}\)，则 \(\bar{M}=X.\)

定义：称度量空间 \((X,d)\) 是可分的，若 \(\exists M\) 为至多可数集（有限集或者可数集），并且 \(\bar{M}=X.\)

这里先介绍几个关于可数集的性质：

例子 1：\(\{0,1\}^{\mathbb{N}}\) 不是可数集！其中 \(\mathbb{N}\) 为自然数集。

例子 2：\((\mathbb{K}^n, d_p)\) 可分。

例子 3：\((\ell^p,d_p)\) 可分，\(M\) 与上面例子 4 的定义相同。

例子 4：\((C[a,b],d_\infty)\) 可分，\(M\) 与上面例子 6 的定义相同。

例子 5：\((\ell^\infty,d_\infty)\) 不可分。

证明：反证法。参考课本 P14，略。

这一部分则开始考虑 \(X\) 中的元素序列，以及序列的极限是否存在、极限是什么的问题。之所以考虑序列这件事情，是因为我们实际中处理问题的时候往往是用序列去逼近一个元素，序列当中的每个元素可能是简单的，二最后去逼近的这个元素往往是不太显然或者比较复杂的东西。这样我们只需要证明序列中的元素满足某些性质，就能证明最后的极限具有某些特殊性质，更容易处理。

我们对序列收敛性的定义是对于 \(x_n,x\in\mathbb{R}\)，称 \(x_n\) 收敛到 \(x\)，记为 \(x_n\to x\) (\(\lim_{n\to\infty} x_n=x\))，若 \(\forall \varepsilon> 0,\exists N,\ \forall n\ge N\)，都有 \(|x_n-x| 0,\exists N, \forall m,n\ge N\)，则 \(d(x_m,x_n) 0,\ \exists \delta > 0\)，使得 \(\forall t\in X_1,\ d_1(t,t_0) 0,\ B(Tx_0,\varepsilon)\subset G\)

由于 \(T\) 连续，则一定 \(\exists \delta > 0\)，使得 \(\forall x\in B(x_0, \delta)\)，都有 \(Tx\in B(Tx_0,\varepsilon)\)，因而 \(B(x_0,\varepsilon)\subset X_1\)

故 \(T^{-1}(G)\) 为开集。

"\(\Longleftarrow\)"：假设 \(\forall G\subset X_2\) 为开集，\(T^{-1}(G)\) 在 \(X_1\) 中也是开集，那么套用连续映射的定义，就能证明 \(T\) 为连续映射。

证毕。

推论：\(T\) 为连续映射 \(\iff \forall F\subset X_2\) 为闭集，那么 \(T^{-1}(F)=\{x\in X_1, Tx\in F\}\) 是 \(X_1\) 中的闭集。

定理：\(T\) 在 \(x_0\) 处连续 \(\iff \forall x_n\in X_1, x_n\to x_0\)，则 \(Tx_n \to Tx_0\)。

证明："\(\Longrightarrow\)"：应用定义；

"\(\Longleftarrow\)"：反证法，假设 \(T\) 在 \(x_0\) 处不连续，

那么 \(\exists \varepsilon_0 > 0,\forall \delta >0, \exists x\in B(x_0, \delta)\)，使得 \(d(Tx_0, Tx) > \varepsilon_0\)

可以取 \(\delta = 1/n\)，由此构造出一个序列 \(x_n \in B(x_0,1/n)\)，

可以知道 \(x_n\to x_0\)，但是却有 \(d(x_n,x_0) \ge \varepsilon_0\)，与假设矛盾。

证毕。

推论：\(T:X_1\to X_2\) 处处连续 \(\iff \forall x_n\to x, Tx_n \to Tx\)。

不动点想必大家在别的地方都或多或少听说过或者用过，应该是解决很多问题的重要工具。在这一部分的内容里面则可以看到，前面讲的序列收敛性、映射在不动点定理当中的应用。

定义：考虑 \(X\ne\varnothing, T:X\to X\)，若 \(x_0\in X,Tx_0=x_0\)，则称 \(x_0\) 为 \(T\) 的不动点。

定义：\(T:X\to X\)，假设 \(\exists 0\le \alpha < 1\)，使得 \(\forall x,y\in X\)，都有 \(d(Tx,Ty) \le \alpha d(x,y)\)，则称 \(T\) 为压缩映射。

定理(Banach不动点定理)：假设 \((X,d)\) 为非空、完备度量空间，\(T:X\to X\) 为压缩映射，则 \(T\) 存在唯一的不动点。

证明：考虑 \(x_0\in X,x_1=Tx_0,\cdots,x_n=Tx_{n-1},\cdots\)，那么可以首先证明 \(x_n\) 为柯西列，进而存在收敛值 \(x\)。 由于 \(d(x_n,x_{n+1})=d(x_n,Tx_n)\to 0\)，从而趋向于 \(x=Tx\)。之后再证明唯一性。证毕。

定理：假设 \((X,d)\) 非空完备，\(T:X\to X\)，设 \(\exists m\ge1\)，\(T^m\) 为压缩映射，则 \(\exists! x\in X\) 使得 \(Tx=x\)。

证明：只需要证明 \(S=T^m\) 的不动点都是 \(T\) 的不动点，反之 \(T\) 的不动点也都是 \(S\) 的不动点即可。

由不动点定理可知，\(S\) 存在唯一一个不动点，记为 \(y_0\)，即 \(Sy_0=y_0\)，那么 \(STy_0=T^{m+1}y_0=TSy_0=Ty_0\)，即 \(Ty_0\) 也是 \(S\) 的不动点，因此一定有 \(Ty_0=y_0\)，即 \(y_0\) 也是 \(T\) 的不动点。假设 \(z_0\) 是 \(T\) 的不动点，那么很容易证明他也是 \(S\) 的不动点。因此 \(T\) 存在唯一不动点。证毕。

例子 1：\(c>0\)，求 \(\sqrt{c}\) 的数值解。可以用数值迭代，取 \(f(x)=(x+\frac{c}{x})/2,D=[\sqrt{c},+\infty)\)，求不动点即可。

例子 2：\((X=\mathbb{K}^n,d_\infty),C\in\mathbb{K}^{n\times n},b\in\mathbb{K}^n\)，映射 \(Tx=Cx+b\)。容易证明若 \(\forall i,\sum_j|a_{ij}|0\)，考虑矩形 \(R=[t_0-a,t_0+a]\times[x_0-b,x_0+b]\)，连续函数 \(f:R\to\mathbb{R}\)，假设存在 \(k\ge0,|f(t,u)-f(t,v)|\le k|u-v|,\forall (t,u),(t,v)\in R\)。考虑初值问题 \[ (P):\begin{cases} x'(t)=f(t,x(t)) \\ x(t_0)=x_0 \end{cases} \] 求上述初值问题的解 \(x(t)\in C[t_0-\beta,t_0+\beta],0