线性代数 |
您所在的位置:网站首页 › 二阶行列式计算原理公式 › 线性代数 |
线性代数
|
系列文章目录
线性代数——行列式线性代数——矩阵线性代数——向量线性代数——线性方程组线性代数——特征值和特征向量线性代数——二次型
文章目录
系列文章目录版权声明补充知识常用希腊字符读音求和公式的性质一元二次方程求解一元三次方程的因式分解数学归纳法等差数列和等比数列的性质
排列行列式行列式的性质重要公式
版权声明
本文大部分内容皆来自李永乐老师考研教材和视频课。 补充知识 常用希腊字符读音 α \alpha α:/ælfə/ β \beta β:/betə/ Γ \Gamma Γ、 γ \gamma γ:/gama/ Δ \Delta Δ、 δ \delta δ:/deltə/ ε \varepsilon ε:/epsilon/ υ \upsilon υ:/apsilon/ θ \theta θ:/θitə/ π \pi π:/paɪ/ η \eta η:/ita/ Λ \Lambda Λ、 λ \lambda λ:/læmdə/ μ \mu μ:/mju/ ξ \xi ξ:/ksi/ Σ \Sigma Σ、 σ \sigma σ:/sigmə/ τ \tau τ:/taʊ/ Φ \varPhi Φ、 φ \varphi φ:/faɪ/ ψ \psi ψ:/psi/ Ω \Omega Ω、 ω \omega ω:/omiga/ ρ \rho ρ:/ru:/ 求和公式的性质 ∑ i = 1 n k a i = k ∑ i = 1 n a i \sum_{i=1}^nka_i=k\sum_{i=1}^na_i i=1∑nkai=ki=1∑nai ∑ i = 1 n ( a i + b i ) = ∑ i = 1 n a i + ∑ i = 1 n b i \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i i=1∑n(ai+bi)=i=1∑nai+i=1∑nbi ∑ i = 1 m ∑ j = 1 n a i j = ∑ j = 1 n ∑ i = 1 m a i j \sum_{i=1}^m\sum_{j=1}^na_{ij}=\sum_{j=1}^n\sum_{i=1}^ma_{ij} i=1∑mj=1∑naij=j=1∑ni=1∑maij 一元二次方程求解
可通过十字相乘法对一元三次方程进行因式分解:
数学归纳法是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。它有以下两种证明形式: 方式一: 验证 n = 1 n=1 n=1时,命题成立假设 n = k n=k n=k时,命题成立证明 n = k + 1 n=k+1 n=k+1时,命题成立 方式二: 验证 n = 1 n=1 n=1和 n = 2 n=2 n=2时命题成立假设 n < k n1) an−an−1=C(n>1) a n a n − 1 = C ( n > 1 ) \frac{a_n}{a_{n-1}}=C(n>1) an−1an=C(n>1)通项公式 a n = a 1 + ( n − 1 ) d a_n=a_1+(n-1)d an=a1+(n−1)d a n = a 1 q n − 1 ( q ≠ 0 ) a_n=a_1q^{n-1}(q\neq0) an=a1qn−1(q=0)性质 m + n = p + q ⇒ a m + a n = a p + a q a n = a m + ( n − m ) d m+n=p+q\Rightarrow a_m+a_n=a_p+a_q\\a_n=a_m+(n-m)d m+n=p+q⇒am+an=ap+aqan=am+(n−m)d m + n = p + q ⇒ a m a n = a p a q a n = a m q n − m m+n=p+q\Rightarrow a_ma_n=a_pa_q\\a_n=a_mq^{n-m} m+n=p+q⇒aman=apaqan=amqn−m前 n n n项和 S n = n ( a 1 + a n ) 2 = n a 1 + n ( n − 1 ) 2 d S_n=\frac{n(a_1+a_n)}{2}=na_1+\frac{n(n-1)}{2}d Sn=2n(a1+an)=na1+2n(n−1)d q ≠ 1 , S = a 1 ( 1 − q n ) 1 − q = a 1 − a n q 1 − q q = 1 , S n = n a 1 q\neq 1,S=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_nq}{1-q}\\q=1,S_n=na_1 q=1,S=1−qa1(1−qn)=1−qa1−anqq=1,Sn=na1 排列由 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n组成的有序数组称为一个 n n n阶排列,通常使用 j 1 j 2 … j n j_1j_2\ldots j_n j1j2…jn表示 n n n阶排列。例如: j 1 j 2 j 3 j 4 = 9527 j_1j_2j_3j_4=9527 j1j2j3j4=9527 在排列中,如果一个大的数排在了一个小的数前面,就称这两个数构成了一个逆序。一个排列逆序的总数称为这个排列的逆序数。通常用 τ ( j 1 j 2 … j n ) \tau(j_1j_2\ldots j_n) τ(j1j2…jn)表示排列 j 1 j 2 … j n j_1j_2\ldots j_n j1j2…jn的逆序数。例如: τ ( 9527 ) = 4 \tau(9527)=4 τ(9527)=4 如果一个排列的逆序数是偶数,则称这个排列是偶排列。如果一个排列的逆序数是奇数,则称这个排列是奇排列。对换是指交换排列中任意两个元素的位置。 如果对一个排列进行奇数次对换那么将改变排列的奇偶性。如果对一个排列进行偶数次对换那么将不会改变排列的奇偶性。一个 n n n阶排列经过对换可以得到 n ! n! n!个不同的排列,并且在这 n ! n! n!个不同的排列中,奇偶排列各占一半。 行列式行列式是不同行不同列 n n n个元素乘积的代数和: D = ∣ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 … a n n ∣ = ∑ j 1 j 2 … j n ( − 1 ) τ ( j 1 j 2 … j n ) a 1 j 1 a 2 j 2 … a n j n D=\begin{vmatrix}a_{11} &a_{12}&\ldots&a_{1n}\\a_{21} &a_{22}&\ldots&a_{2n}\\\vdots&\vdots&&\vdots&\\a_{n1}&a_{n2}&\ldots&a_{nn}\end{vmatrix}=\sum_{j_1j_2\ldots j_n}(-1)^{\tau(j_1j_2\ldots j_n)}a_{1j_1}a_{2j_2}\dots a_{nj_n} D= a11a21⋮an1a12a22⋮an2………a1na2n⋮ann =j1j2…jn∑(−1)τ(j1j2…jn)a1j1a2j2…anjn 这个式子称为 n n n阶行列式的完全展开式,共有 n ! n! n!项。对于二阶三阶行列式有对角线法则: 2阶行列式: ∣ a b c d ∣ = a d − b c \begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc acbd =ad−bc3阶行列式: ∣ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ = a 1 b 2 c 3 + a 2 b 3 c 1 + a 3 b 1 c 2 − a 3 b 2 c 1 − a 2 b 1 c 3 − a 1 b 3 c 2 \begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix}=a_1b_2c_3+a_2b_3c_1+a_3b_1c_2-a_3b_2c_1-a_2b_1c_3-a_1b_3c_2 a1b1c1a2b2c2a3b3c3 =a1b2c3+a2b3c1+a3b1c2−a3b2c1−a2b1c3−a1b3c2将行列式的第 i i i行和第 j j j列去掉,那么剩下的行列式就是 a i j a_{ij} aij的余子式,记为 M i j M_{ij} Mij并记 A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij为 a i j a_{ij} aij的代数余子式。 行列式的性质 某行有公因式 k k k,可把公因式 k k k提到行列式外: ∣ … … … … k a i 1 k a i 2 … k a i n … … … … ∣ = k ∣ … … … … a i 1 a i 2 … a i n … … … … ∣ \begin{vmatrix} \dots&\dots&\dots&\dots\\ ka_{i1}&ka_{i2}&\dots&ka_{in}&\\ \dots&\dots&\dots&\dots \end{vmatrix} = k\begin{vmatrix} \dots&\dots&\dots&\dots\\ a_{i1}&a_{i2}&\dots&a_{in}&\\ \dots&\dots&\dots&\dots \end{vmatrix} …kai1……kai2……………kain… =k …ai1……ai2……………ain… 特别的:某行元素全为零,则行列式为 0 0 0。对换行列式某两行的位置,行列式变号。特别的: 两行相等,行列式为 0 0 0,即 D = − D , D = 0 D=-D,D=0 D=−D,D=0两行成比例,行列式为 0 0 0,即 k D = − k D , D = 0 kD=-kD,D=0 kD=−kD,D=0 某行所有元素都是两个数的和,则可写成两个行列式之和: ∣ a 1 + b 1 a 2 + b 2 a 3 + b 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ = ∣ a 1 a 2 a 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ + ∣ b 1 b 2 b 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ \begin{vmatrix}a_1+b_1&a_2+b_2&a_3+b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}=\begin{vmatrix}a_1&a_2&a_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix}+\begin{vmatrix}b_1&b_2&b_3\\c_1&c_2&c_3\\d_1&d_2&d_3\end{vmatrix} a1+b1c1d1a2+b2c2d2a3+b3c3d3 = a1c1d1a2c2d2a3c3d3 + b1c1d1b2c2d2b3c3d3 行列式某行的 k k k倍加至另一行,行列式不变: ∣ a 1 + k b 1 a 2 + k b 2 a 3 + k b 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ = ∣ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ + k ∣ b 1 b 2 b 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ = ∣ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ \begin{vmatrix} a_1+kb_1&a_2+kb_2&a_3+kb_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} = \begin{vmatrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} {+}k \begin{vmatrix} b_1&b_2&b_3\\b_1&b_2&b_3\\c_1&c_2&c_3 \end{vmatrix} = \begin{vmatrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{vmatrix} a1+kb1b1c1a2+kb2b2c2a3+kb3b3c3 = a1b1c1a2b2c2a3b3c3 +k b1b1c1b2b2c2b3b3c3 = a1b1c1a2b2c2a3b3c3 按行按列展开式: 按 i i i行展开: D = a i 1 A i 1 + a i 2 A i 2 + … + a i n A i n = ∑ j = 1 n a i j A i j D=a_{i1}A_{i1}+a_{i2}A_{i2}+\ldots+a_{in}A_{in}=\sum_{j=1}^na_{ij}A_{ij} D=ai1Ai1+ai2Ai2+…+ainAin=j=1∑naijAij按 j j j列展开: D = a 1 j A 1 j + a 2 j A 2 j + … + a n j A n j = ∑ i = 1 n a i j A i j D =a_{1j}A_{1j}+a_{2j}A_{2j}+\ldots+a_{nj}A_{nj}=\sum_{i=1}^na_{ij}A_{ij} D=a1jA1j+a2jA2j+…+anjAnj=i=1∑naijAij 某一行(列)的所有元素与另一行(列)相应元素的代数余子式乘积之和等于 0 0 0: a 11 A 31 + a 12 A 32 + a 13 A 33 = 0 a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33}=0\\ a11A31+a12A32+a13A33=0 证明:已知 D = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ D= \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{vmatrix} D= a11a21a31a12a22a32a13a23a33 构造以下行列式: F = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 11 a 12 a 13 ∣ = 0 = a 11 A 31 + a 12 A 32 + a 13 A 33 F= \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{11}&a_{12}&a_{13} \end{vmatrix} =0 =a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33} F= a11a21a11a12a22a12a13a23a13 =0=a11A31+a12A32+a13A33 因为 F F F的 A 31 A_{31} A31, A 32 A_{32} A32, A 33 A_{33} A33和 D D D的相等,所以: a 11 A 31 + a 12 A 32 + a 13 A 33 = 0 a_{11}A_{31}+a_{12}A_{32}+a_{13}A_{33}=0\\ a11A31+a12A32+a13A33=0 重要公式 上(下)三角行列式的值: ∣ a 11 a 12 … a 1 n 0 a 22 … a 2 n ⋮ ⋮ ⋮ 0 0 … a n n ∣ = ∣ a 11 0 … 0 a 21 a 22 … 0 ⋮ ⋮ ⋮ a n 1 a n 2 … a n n ∣ = a 11 a 22 … a n n \begin{vmatrix}a_{11}&a_{12}&\ldots& a_{1n}\\0&a_{22}&\ldots&a_{2n}\\\vdots&\vdots&&\vdots\\0&0&\ldots&a_{nn}\end{vmatrix}=\begin{vmatrix}a_{11}&0&\ldots& 0\\a_{21}&a_{22}&\ldots&0\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\ldots&a_{nn}\end{vmatrix}=a_{11}a_{22}\dots a_{nn} a110⋮0a12a22⋮0………a1na2n⋮ann = a11a21⋮an10a22⋮an2………00⋮ann =a11a22…ann副对角线行列式的值: ∣ a 11 a 12 … a 1 n a 21 a 22 … 0 ⋮ ⋮ ⋮ a n 1 0 … 0 ∣ = ∣ 0 … 0 a 1 n 0 … a 2 ( n − 1 ) a 2 n ⋮ ⋮ ⋮ a n 1 … a n ( n − 1 ) a n n ∣ = ( − 1 ) n ( n − 1 ) 2 a 1 n a 2 ( n − 1 ) … a n 1 \begin{vmatrix}a_{11}&a_{12}&\ldots& a_{1n}\\a_{21}&a_{22}&\ldots&0\\\vdots&\vdots&&\vdots\\a_{n1}&0&\ldots&0\end{vmatrix}=\begin{vmatrix}0&\dots&0& a_{1n}\\0&\dots&a_{2(n-1)}&a_{2n}\\\vdots&&\vdots&\vdots\\a_{n1}&\dots&a_{n(n-1)}&a_{nn}\end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2(n-1)}\dots a_{n1} a11a21⋮an1a12a22⋮0………a1n0⋮0 = 00⋮an1………0a2(n−1)⋮an(n−1)a1na2n⋮ann =(−1)2n(n−1)a1na2(n−1)…an1范德蒙行列式: ∣ 1 1 … 1 a 1 a 2 … a n a 1 2 a 2 2 … a n 2 ⋮ ⋮ ⋮ a 1 n − 1 a 2 n − 1 … a n n − 1 ∣ = ∏ 1 ≤ j < i ≤ n ( a i − a j ) \begin{vmatrix} 1&1&\dots&1\\ a_1&a_2&\dots&a_n\\ a_1^2&a_2^2&\dots&a_n^2\\ \vdots&\vdots&&\vdots\\ a_1^{n-1}&a_2^{n-1}&\dots&a_n^{n-1} \end{vmatrix} = \prod_{1≤j |
【本文地址】
今日新闻 |
推荐新闻 |

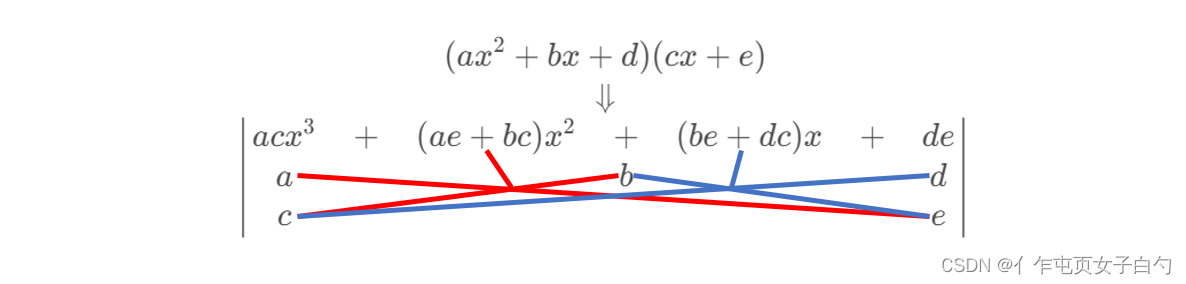 下面以一个例子说明十字相乘法的步骤:
2
x
3
−
3
x
2
−
11
x
−
3
2x^3-3x^2-11x-3
2x3−3x2−11x−3
下面以一个例子说明十字相乘法的步骤:
2
x
3
−
3
x
2
−
11
x
−
3
2x^3-3x^2-11x-3
2x3−3x2−11x−3