【高等数学】四.多元函数微分学和二重积分 |
您所在的位置:网站首页 › 二重积分的定义计算 › 【高等数学】四.多元函数微分学和二重积分 |
【高等数学】四.多元函数微分学和二重积分
|
多元函数微分学
一、基本概念
需要熟练掌握概念的描述,容易考选择题。 1.平面点集的概念正向证明有点难,可以反向证伪 lim x → x 0 , y → y 0 ( x , y ) = A \lim_{x\to x_0,y\to y_0}(x,y) = A x→x0,y→y0lim(x,y)=A 多元微分下洛必达、泰勒展开、单调有界准则不可用 并且极限会排除不存在的路径,要求的是每个方向的极限都存在并且相等 因此求极限是否存在,关键在于是否存在特殊路径,使得极限不一致 3.连续lim x → x 0 , y → y 0 ( x , y ) = f ( x 0 , y 0 ) \lim_{x\to x_0,y\to y_0}(x,y) = f(x_0,y_0) x→x0,y→y0lim(x,y)=f(x0,y0) 如果f(x,y)在闭区域D上连续,则f(x,y)在D上有界 4.偏导数lim Δ x → 0 f ( x 0 + Δ x , y 0 ) + f ( x 0 , y 0 ) Δ x \lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)+f(x_0,y_0)}{\Delta x} Δx→0limΔxf(x0+Δx,y0)+f(x0,y0) 存在,则称此为极限f(x,y)对x的偏导 TIPS 二阶偏导数 f x y ′ f ( x , y ) f'_{xy}f(x,y) fxy′f(x,y)和 f y x ′ f ( x , y ) f'_{yx}f(x,y) fyx′f(x,y)是同样的在 f ( x , y 0 ) = 0 f(x,y_0)=0 f(x,y0)=0的情况下, f x ′ ( x , y 0 ) = [ f ( x , y 0 ) ] x ′ = f x ′ ( x , y ) ∣ y = y 0 f'_x(x,y_0)=[f(x,y_0)]'_x=f'_x(x,y)|_{y=y_0} fx′(x,y0)=[f(x,y0)]x′=fx′(x,y)∣y=y0注意:多元微分中的 ∂ z ∂ x \frac{∂z}{∂x} ∂x∂z不可拆分看成 ∂ z ∂z ∂z除以 ∂ x ∂x ∂x,这和一元函数中的 d z d x \frac{dz}{dx} dxdz不一样,数值上 ∂ z ∂ x \frac{∂z}{∂x} ∂x∂z和 F x ′ F z ′ \frac{F'_x}{F'_z} Fz′Fx′一样 5.偏导数连续对于z=f(x,y)讨论在某特殊点(x0,y0)是否连续,其步骤为: 用定义法求 f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) f'_x(x_0,y_0), f'_y(x_0,y_0) fx′(x0,y0),fy′(x0,y0)用公式法求 f x ′ ( x , y ) , f y ′ ( x , y ) f'_x(x,y), f'_y(x,y) fx′(x,y),fy′(x,y)计算 lim x → x 0 , y → y 0 f x ′ ( x , y ) \lim_{x\to x_0, y\to y_0}f'_x(x,y) limx→x0,y→y0fx′(x,y)和 lim x → x 0 , y → y 0 f y ′ ( x , y ) \lim_{x\to x_0, y\to y_0}f'_y(x,y) limx→x0,y→y0fy′(x,y),分别比较是否和 f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) f'_x(x_0,y_0), f'_y(x_0,y_0) fx′(x0,y0),fy′(x0,y0)相等,如果相等则在点(x0,y0)处偏导数连续∂x和dx的区别是什么?TIPS:求极限的时候,可以将极限已确认的部分提出用于简化计算 6.可微分全增量减去各个自变量的偏增量部分的极限为0则可微分 求可微的步骤: 写出全增量 Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0, y_0) Δz=f(x0+Δx,y0+Δy)−f(x0,y0)写出线性增量 A Δ x + B Δ y A\Delta x+B\Delta y AΔx+BΔy,其中 Δ x = f x ′ ( x 0 , y 0 ) , Δ y = f y ′ ( x 0 , y 0 ) \Delta x=f'_x(x_0,y_0),\Delta y=f'_y(x_0,y_0) Δx=fx′(x0,y0),Δy=fy′(x0,y0)作极限 lim Δ x → x 0 , Δ y → y 0 Δ z − ( A Δ x + B Δ y ) ( Δ x ) 2 + ( Δ y ) 2 \lim_{\Delta x \to x_0, \Delta y \to y_0}\frac{\Delta z-(A\Delta x+B\Delta y)}{\sqrt {(\Delta x)^2+(\Delta y)^2}} Δx→x0,Δy→y0lim(Δx)2+(Δy)2 Δz−(AΔx+BΔy)如果极限为0,则可微,反之则不可微TIPS:在第3步判断是否可微的时候,如果最后的结果有两个变量不好计算,可以取特殊路径,比如令 x → x 0 , y → k x x\to x_0, y\to kx x→x0,y→kx 二、多元微分计算 2.1复合函数求导法 1.链式求导规则
比如对于y=f(u), u=g(x),有
y
x
′
=
y
u
′
⋅
u
x
′
y'_x=y'_u\cdot u'_x
yx′=yu′⋅ux′,也可以表示为:
d
y
=
y
u
′
d
u
=
y
x
′
d
x
dy=y'_udu=y'_xdx
dy=yu′du=yx′dx,这个是一元微分的不变性 此法又称为隐函数存在定理 设F(x,y,z)=0,在点P0(x0,y0,z0)处满足 F ( P 0 ) = 0 F(P_0)=0 F(P0)=0并且 F z ′ ( P 0 ) ≠ 0 F'_z(P_0)\neq 0 Fz′(P0)=0则在P0的某邻域内可确定z=z(x,y)并且有 ∂ z ∂ x = − F x ′ F z ′ , ∂ z ∂ y = − F y ′ F z ′ \frac{∂z}{∂x}=-\frac{F'_x}{F'_z},\frac{∂z}{∂y}=-\frac{F'_y}{F'_z} ∂x∂z=−Fz′Fx′,∂y∂z=−Fz′Fy′
多元微分的计算的三大基本思路是:1.链式求导规则2.隐函数存在定理(公式法)还有3.全微分形式不变性 隐函数定理:由隐函数推导出普通函数及其微分的定理 对于一般的多元微分计算,考虑三种方法:公式法、全微分、偏微分求导法 TIPS: 对于难以求偏导的,可以使用先代入具体点,后求解。这一点不只是可以用于一阶求导,也可以在知道一阶导数,但是二阶导数求导十分复杂时用于简化二阶导数式子。这种方法可用范围十分广泛,包括隐函数都能用幂指函数多元微分:换元法、对数化(两边加ln)、指数化对于拉格朗日乘数法求条件极值仍需要加强理解,以及30讲练习11.5如果出现微分难以计算,可以试试交换下求导次序对于一些求微分的题目,可以试试将其转化为隐函数然后使用公式法,可能会更快注意:多元微分中的 ∂ z ∂ x \frac{∂z}{∂x} ∂x∂z不可拆分看成 ∂ z ∂z ∂z除以 ∂ x ∂x ∂x,这和一元函数中的 d z d x \frac{dz}{dx} dxdz不一样,数值上 ∂ z ∂ x \frac{∂z}{∂x} ∂x∂z和 F x ′ F z ′ \frac{F'_x}{F'_z} Fz′Fx′一样 三、极值和最值问题三大考察点:概念、无条件极值、有条件极值 3.1 无条件极值先找必要条件: 点X0(x0,y0)使得f’x(x0,y0)=f’y(x0,y0)=0,则点X0为驻点,是可能的极值点 再找充分条件 令 { f x x ′ ′ ( x 0 , y 0 ) = A > 0 f x y ′ ′ ( x 0 , y 0 ) = f y x ′ ′ ( x 0 , y 0 ) = B f y y ′ ′ ( x 0 , y 0 ) = C \left\{ \begin{aligned} f''_{xx}(x_0,y_0) & = A>0 \\ f''_{xy}(x_0,y_0) & = f''_{yx}(x_0,y_0)=B \\ f''_{yy}(x_0,y_0) & = C \end{aligned} \right. ⎩⎪⎨⎪⎧fxx′′(x0,y0)fxy′′(x0,y0)fyy′′(x0,y0)=A>0=fyx′′(x0,y0)=B=C 当 Δ = A C − B 2 > 0 \Delta=AC-B^2>0 Δ=AC−B2>0并且 f x x ′ ′ > 0 f''_{xx}>0 fxx′′>0时, f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)为极小值当 Δ = A C − B 2 > 0 \Delta=AC-B^2>0 Δ=AC−B2>0并且 f x x ′ ′ < 0 f''_{xx} |
【本文地址】
今日新闻 |
推荐新闻 |


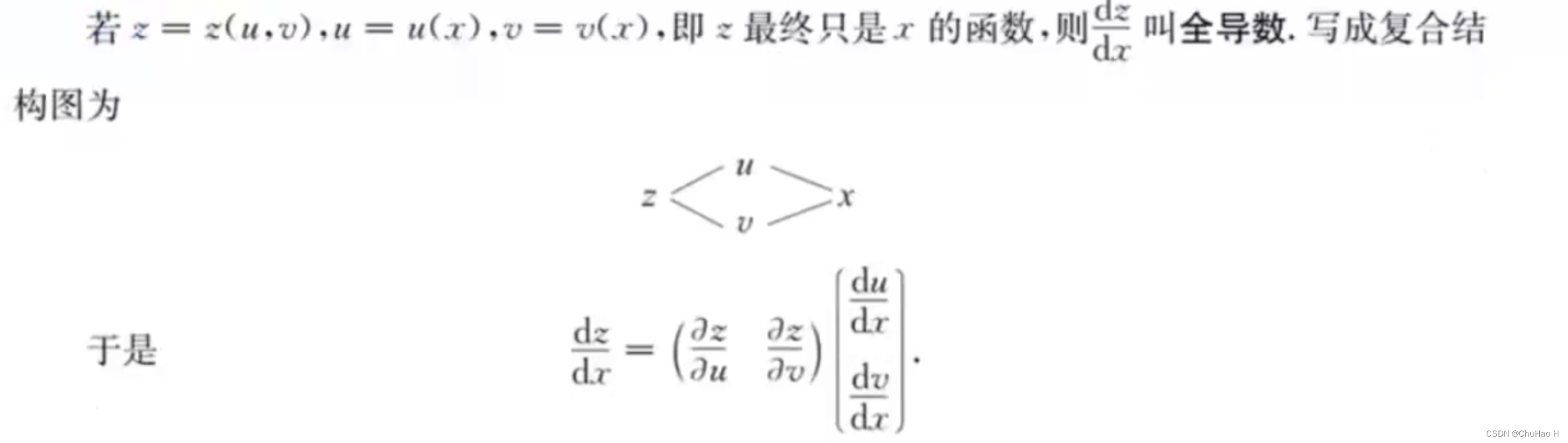
 全微分形式不变指出:全微分既可以用最终变量表示,也可以用中间变量表示。这使得微分的表示不一定要用最终的x,y表示,也可以用中间变量u,v表示,从而隐藏了一部分复杂的关系细节,在复合关系难以理清的时候,可以使用。
全微分形式不变指出:全微分既可以用最终变量表示,也可以用中间变量表示。这使得微分的表示不一定要用最终的x,y表示,也可以用中间变量u,v表示,从而隐藏了一部分复杂的关系细节,在复合关系难以理清的时候,可以使用。
