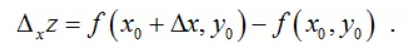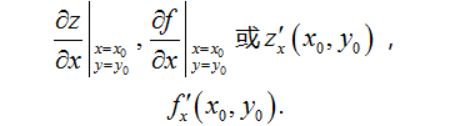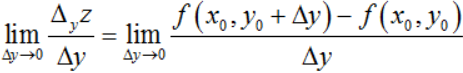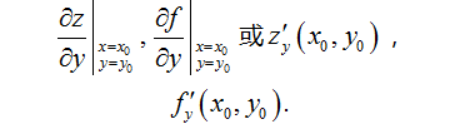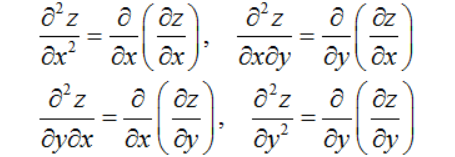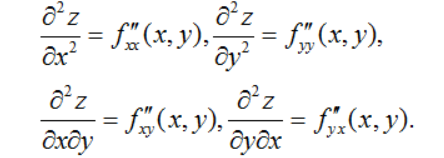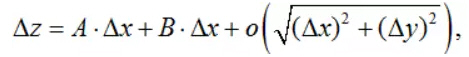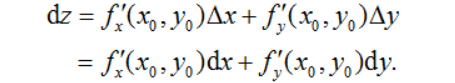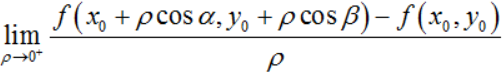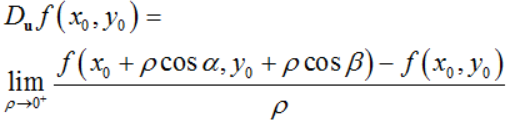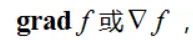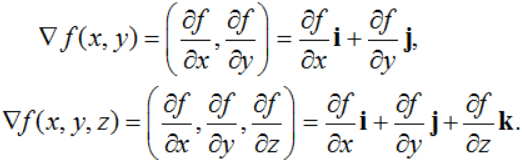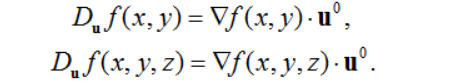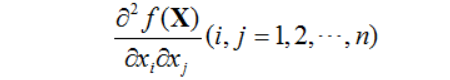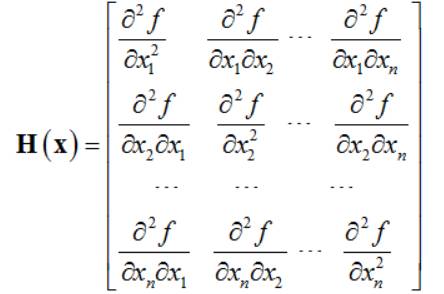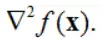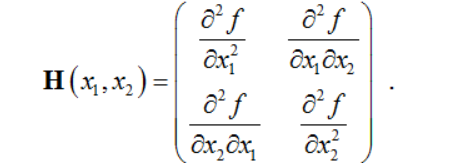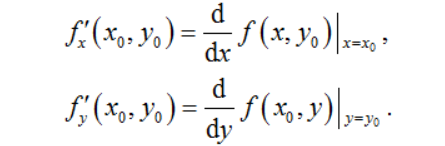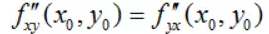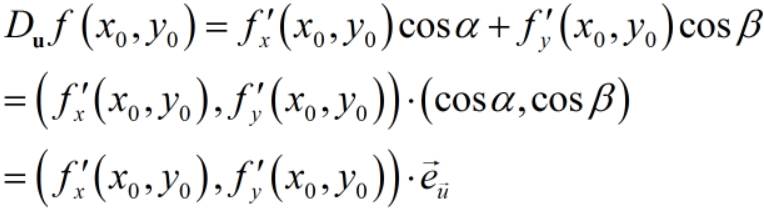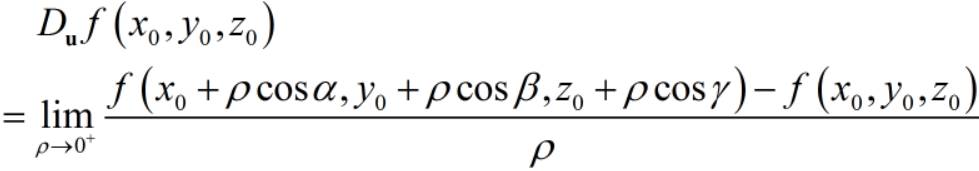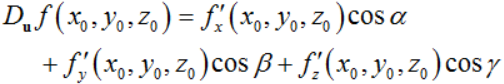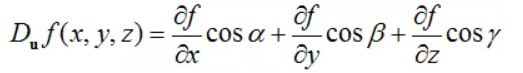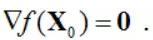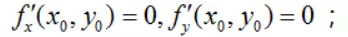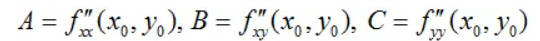2．二元函数的几何表示

若二元函数z=f(x,y)的定义域为区域D，那么，它在几何上就表示三维空间中的一张曲面，在xOy平面上可以描述为区域D上的等值线图。

3. 二元函数偏导数的定义

设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义，当y固定在y0而x在x0处有增量△x时，相应地函数有关于x的偏增量

如果极限

存在，则称此极限为函数z=f(x,y)在点(x0,y0)处关于自变量x的偏导数，记作

类似地，称极限

为函数z=f(x,y)在点(x0,y0)处关于自变量y的偏导数，记作

4．二阶偏导数的定义

二元函数f(x,y)在区域D上的偏导数仍然是自变量x,y的函数，因此，进一步，对这两个偏导函数分别对x,y求偏导数，就产生下列四个二阶偏导数：

分别记作

5．全增量与全微分

设函数z=f(x,y)在点(x0,y0)的某邻域内有定义，(x,y)为该邻域内的任意一点，记x=x0+△x,y=y0+△y,则自变量(x0,y0)变化到(x,y)的全增量为

△z=f(x0+△x,y0+△y)-f(x,y).

如果函数z=f(x,y)在点(x0,y0)可微，则函数的全增量可以表示为

其中A,B是与自变量的增量△x,△y无关的量，并且把去掉无穷小量的部分称为函数的全微分，并记作dz，即有

dz=A·△x+ B·△y.

并且有

函数可微⇒函数连续，且偏导数存在；

偏导数连续⇒函数可微

也就可以推出z=f(x,y)在点(x0,y0)的全微分为：

6．方向导数的定义

设二元函数z=f(x,y)在点(x0,y0)的某邻域内有定义，其中向量u对应的单位向量为uo=(cosα,cosβ)，其中α, β为向量u的方向角，则当极限

存在时，则称该极限为函数z=f(x,y)在点(x0,y0)处沿方向u的方向导数，记作

方向导数也记作∂f/∂u|(x0,y0).

【注】从实际应用与通用性角度，我们定义方向导数ρ→0+。有些教材对方向导数的定义ρ的取值可正可负，虽然可以视偏导数为其特殊情况，但是其条件对于实际应用来说太强！当然如果一个函数沿着指定方向及其反方向方向导数存在且互为相反数，则定义与ρ→0+一样可得得到有效结论。

方向导数的几何意义: Duf(x0,y0)表示过点P(x0,y0,0),M(x0,y0,f(x0,y0))，且平行于xOy面上的向量u和垂直于xOy的平面π与曲面S的交线在点M(x0,y0,f(x0,y0))处的切线的斜率．

【注】特别地，f’x(x0,y0)与f’y(x0,y0)分别为函数f(x,y)在点P(x0,y0)处沿两坐标轴方向i=(1,0)及j=(0,1)的方向导数．

7．梯度

二元函数f(x,y)与三元函数f(x,y,z)的梯度（梯度向量），记作

分别定义为：

【注】方向导数是函数梯度在方向向量u上的投影：

8．海赛(黑塞)矩阵

设n元函数f(X)在点X处对于自变量的各分量的二阶偏导数

连续，则称矩阵

为f(X)在点X处的二阶导数或黑塞矩阵(Hessian Matrix)，也可记作

【注】矩阵H为对称矩阵．

当n=2时，由二元函数f(x1,x2)的所有二阶偏导数构成的黑塞矩阵为

由二元函数f(x1,x2)的所有二阶偏导数组成．

9．极值的定义

设n元函数f(X)在X0的某邻域内有定义，如果对于该邻域内任何异于X0的点X，都有

f(X)f(X0)，

则称函数f(X)在X0处取得极小值f(X0)，称点X0为f(X)的极小值点．

10．条件极值相关的概念

在实际中会遇到求一个函数f(x,y)在满足约束条件g(x,y)=0下的极值问题，我们称之为条件极值问题．通常，称函数f(x,y)为目标函数，方程g(x,y)=0为约束条件，变量x,y为决策变量．相应地，把求一个函数的，只有定义域限制的（不带条件的）极值问题为无条件极值问题．

二、相关定理与结论

1．具体函数偏导函数的计算

对于非间断点处，使用一元函数求导运算法则求多元函数关于某个变量的偏导数；对于间断点的偏导数使用偏导数的定义判断偏导数的存在性，并计算偏导数:

2．混合偏导数相等的判定定理

定理如果函数z=f(x,y)的两个混合偏导数在点(x0,y0)处连续，则

【注1】对于分段函数的导函数或高阶导数在分界点的连续性和可导性的讨论，以及导数值的计算，一般都要先计算得到该函数的导函数以后，然后再使用定义的方法对分界点的连续性和可导性进行判定，或完成相关的计算。

【注2】由于二元初等函数及其各阶偏导数在其定义区域内连续，因而在定义区域内二元初等函数的二阶混合偏导数与x，y的先后次序无关．

3．方向导数的存在性判定与计算公式

定理设函数f(x,y)在点P(x0,y0)可微，那么函数在该点沿任意方向向量u的方向导数都存在，且有

其中cosα,cosβ为向量u的方向余弦．

方向导数的概念及计算公式可推广到三元及三元以上的函数．例如，三元函数f(x,y,z)在点P(x0,y0,z0)沿方向u（对应的单位向量为uo=(cosα,cosβ,cosγ)）的方向导数定义为

同样，当函数f(x,y,z)在点P(x0,y0,z0)可微时，函数在该点沿方向u的方向导数

一般地，当函数f(x,y,z)可微时，有

4．可微函数取极值的必要条件

定理设n元函数f(X)在点X0处对各个自变量的一阶偏导数都存在，且在点X0处取极值，则有

(1) 点X0称为函数f(X)的驻点或稳定点，所以具有一阶偏导数的n元函数，其极值点必定是驻点．

(2) 假设函数f(X)在X0处可微，X0为f(X)的驻点，如果在X0的任何邻域内既存在函数值大于f(X0)的点也存在函数值小于f(X0)的点，即X0不为极值点，则称X0为函数f(X)的鞍点。

(3) 可微函数z=f(x,y)在极值点(x0,y0)处有水平切平面，且切平面方程为

z=f(x0,y0).

5．可微函数取极值的充分条件

定理设n元函数f(X)在点X0处具有二阶连续偏导数，且

记H(X0)为f(X)在点X0处的黑塞矩阵．

(1) 如果H(X0)正定，则X0为f(X)的极小值点；

(2) 如果H(X0)负定，则X0为f(X)的极大值点；

(3) 如果H(X0)不定，则X0为f(X)的鞍点；

(4) 其他情况需要另行判定(半正定，半负定)．

6．二元函数极值判定的充分条件

定理设二元函数z=f(x,y)在(x0,y0)处具有二阶连续的偏导数，且

并记

则有

(1) 如果A>0，且AC-B2>0，则f(x,y)在(x0,y0)处取极小值；

(2) 如果A0，则f(x,y)在(x0,y0)处取极大值；

(3) 如果AC-B20)与x的负向，即y=0(x0)与y的负向，即x=0(y0，则u是f(X)在点X0处的一个上升方向；如果Duf(X0)