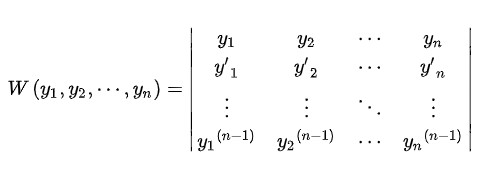定义

​ 微分方程是一种数学方程，用来描述某一类函数与其导数之间的关系；含导数或微分的方程称之为微分方程，一般形式为f(x,y’,…y(n)) = 0

方程的阶数

​ 微分方程所含的导数或微分的最高阶数称为微分方程的阶数

方程的解

几种类型

例题1

例题2

例题3

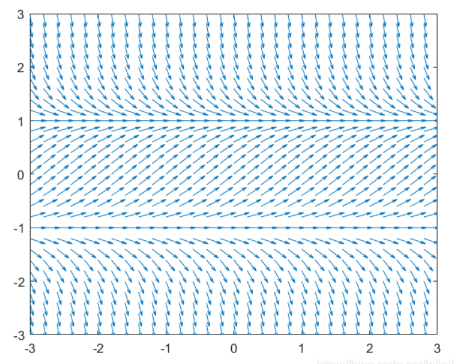
定义：在每一点(x,y)都画上以值f(x,y)为斜率中心在点(x,y)的线段，就得到一个方向场。

意义：尽管我们不一定能求出方程的解，但我们可知道解曲线在区域任意点(x,y)的斜率，这对微分方程的近似解和研究其几何性质极为重要。

设一阶微分方程 d y d x = f ( x , y ) \frac{dy}{dx} = f(x,y) dxdy​=f(x,y)，满足解的存在唯一性定理的条件，有且仅有一个解y=y(x)。则向量场由无数个在点(x,y)的斜率的线段组成

微分方程 y ′ = 1 − y 2 y' = 1- y^2 y′=1−y2，x ∈ [ − 3 , 3 ] $ x \in [-3,3]x∈[−3,3] ,y ∈ [ − 3.3 ] y\in [-3.3]y∈[−3.3]$,步长为 h = 0.2 h=0.2h=0.2,箭头长为 c = 0.01

定义 对 一 阶 微 分 方 程 d y d x = f ( x , y ) , 若 f ( x , y ) = g 1 ( x ) g 2 ( y ) , 其 中 g 1 ( x ) , g 2 ( y ) 是 关 于 x ， y 的 连 续 函 数 ， 称 d y d x = f ( x , y ) 为 可 分 离 变 量 的 微 分 方 程 对一阶微分方程 \frac { dy } { dx } = {f ( x , y )},若{f ( x , y )} = g _ { 1 } ( x ) g _ { 2 } ( y ),其中g_1(x),g_2(y)是关于x，y的连续函数，称\frac { dy } { dx } = {f ( x , y )}为可分离变量的微分方程 对一阶微分方程dxdy​=f(x,y),若f(x,y)=g1​(x)g2​(y),其中g1​(x),g2​(y)是关于x，y的连续函数，称dxdy​=f(x,y)为可分离变量的微分方程 解法 （分离变量——两边积分） d y d x = f ( x , y )   − > d y d x = g ( x ) g 2 ( y )   − > d y g ( y ) = g 1 ( x ) d x , 两 边 积 分 得 ∫ d y g 2 ( y ) = g 1 ( x ) d x + C \frac { dy } { dx } = {f ( x , y )} \ -> \frac { dy } { dx } = g ( x ) g _ { 2 } ( y ) \ -> \frac { dy } { g ( y ) } = g _ { 1 } ( x ) dx,两边积分得\int \frac { dy } { g _ { 2 } ( y ) } = g _ { 1 } ( x ) dx + C dxdy​=f(x,y) −>dxdy​=g(x)g2​(y) −>g(y)dy​=g1​(x)dx,两边积分得∫g2​(y)dy​=g1​(x)dx+C

【例】求 d y d x = 1 + x + y 2 + x y 2 \frac { dy } { dx } = 1 + x + y ^ { 2 } + xy ^ { 2 } dxdy​=1+x+y2+xy2 的通解。 【解】 由 d y d x = 1 + x + y 2 + x y 2 \frac { dy } { dx } = 1 + x + y ^ { 2 } + xy ^ { 2 } dxdy​=1+x+y2+xy2,得 d y d x = ( 1 + x ) ( 1 + y 2 ) \frac { dy } { dx } = ( 1 + x ) ( 1 + y ^ { 2 } ) dxdy​=(1+x)(1+y2) ,分离变量得 d y 1 + y 2 = ( 1 + x ) d x \frac { dy } { 1 + y ^ { 2 } } = ( 1 + x ) dx 1+y2dy​=(1+x)dx,两边积分,得通解为 a r c tan ⁡ y = x + 1 2 x 2 + c ( c arc \tan y = x + \frac { 1 } { 2 } x ^ { 2 } + c ( c arctany=x+21​x2+c(c为任意常数)

形如 d y d x = a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 \frac { dy } { dx } = \frac { a _ { 1 } x + b _ { 1 } y + c _ { 1 } } { a _ { 2 } x + b _ { 2 } y + c _ { 2 } } dxdy​=a2​x+b2​y+c2​a1​x+b1​y+c1​​ 的方程经过变量变换转化为变量分离方程

三种情况  (1)  a 1 a 2 = b 1 b 2 = c 1 c 2 = k (  常数  )  情形.   这时方程化为  d y d x = k  有通解  y = k x + c  (c为任意常数)   (2)  a 1 a 2 = b 1 b 2 = k ≠ c 1 c 2  情形   令  u = a 2 x + b 2 y ,  这时有  a 1 x + b 1 y = k ( a 2 x + b 2 y ) d u   d x = a 2 + b 2 d y   d x = a 2 + b 2 k u + c 1 u + c 2  是变量分离方程.   (3)  a 1 a 2 ≠ b 1 b 2  情形.   如果方程中 c 1 , c 2  不全为零,方程右端分子、分母都是 x, y 的一次多项式,因此  { a 1 x + b 1 y + c 1 = 0 , a 2 x + b 2 y + c 2 = 0  代表 Oxy平面上两条相交的直线,设交点为  ( α , β )  若令  { X = x − α , Y = y − β ,    则 有   { a 1 X + b 1 Y = 0 , a 2 X + b 2 Y = 0 ,  从而原方程变为   d Y   d X = a 1 X + b 1 Y a 2 X + b 2 Y = g ( Y X ) 再 令 U = X Y .  因此, 求解上述变量分离方程, 最后代回原变量即可得原方程的解  \begin{array}{l} \text { (1) } \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}=k(\text { 常数 }) \text { 情形. } \\ \text { 这时方程化为 } \frac{dy}{dx}=k \text { 有通解 } y = kx + c \text { (c为任意常数) } \\ \text { (2) } \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=k \neq \frac{c_{1}}{c_{2}} \text { 情形 } \\ \text { 令 } u=a_{2} x+b_{2} y, \text { 这时有 } a_1x+b_1y=k(a_2x+b_2y)\\ \quad \frac{\mathrm{d} u}{\mathrm{~d} x}=a_{2}+b_{2} \frac{\mathrm{d} y}{\mathrm{~d} x}=a_{2}+b_{2} \frac{k u+c_{1}}{u+c_{2}} \text { 是变量分离方程. } \\ \text { (3) } \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \text { 情形. } \\ \text { 如果方程中} c_{1}, c_{2} \text { 不全为零,方程右端分子、分母都是 x, y 的一次多项式,因此 } \\ \qquad \left\{\begin{array}{l}a_{1} x+b_{1} y+c_{1}=0, \\ a_{2} x+b_{2} y+c_{2}=0\end{array}\right. \\ \text { 代表 Oxy平面上两条相交的直线,设交点为 }(\alpha, \beta) \\ \text { 若令 } \begin{array}{l} \left\{\begin{array}{l}X=x-\alpha, \\ Y=y-\beta,\end{array}\right.\end{array} \ \ 则有 \ \left\{\begin{array}{l}a_{1} X+b_{1} Y=0, \\ a_{2} X+b_{2} Y=0,\end{array}\right. \\ \text { 从而原方程变为 } \ \begin{array}{l}\frac{\mathrm{d} Y}{\mathrm{~d} X}=\frac{a_{1} X+b_{1} Y}{a_{2} X+b_{2} Y}=g\left(\frac{Y}{X}\right)再令U=\frac{X}{Y}. \end{array} \\ \text { 因此, 求解上述变量分离方程, 最后代回原变量即可得原方程的解 } \end{array}  (1) a2​a1​​=b2​b1​​=c2​c1​​=k( 常数 ) 情形.  这时方程化为 dxdy​=k 有通解 y=kx+c (c为任意常数)  (2) a2​a1​​=b2​b1​​=k​=c2​c1​​ 情形  令 u=a2​x+b2​y, 这时有 a1​x+b1​y=k(a2​x+b2​y) dxdu​=a2​+b2​ dxdy​=a2​+b2​u+c2​ku+c1​​ 是变量分离方程.  (3) a2​a1​​​=b2​b1​​ 情形.  如果方程中c1​,c2​ 不全为零,方程右端分子、分母都是 x, y 的一次多项式,因此 {a1​x+b1​y+c1​=0,a2​x+b2​y+c2​=0​ 代表 Oxy平面上两条相交的直线,设交点为 (α,β) 若令 {X=x−α,Y=y−β,​​  则有 {a1​X+b1​Y=0,a2​X+b2​Y=0,​ 从而原方程变为   dXdY​=a2​X+b2​Ya1​X+b1​Y​=g(XY​)再令U=YX​.​ 因此, 求解上述变量分离方程, 最后代回原变量即可得原方程的解 ​

例题1

求解微分方程 y ′ = x + y + 4 x − y − 6 y' = \frac{x+y+4}{x-y-6} y′=x−y−6x+y+4​

【解】令 { x + y + 4 = 0 x − y − 6 = 0 \{ \begin{array} { l } { { x + y + 4 = 0 } } \\ { { x - y - 6 = 0 } } \\ \end{array} {x+y+4=0x−y−6=0​，可得x=1，y=-5，令 { X = x − 1 Y = y + 5 . \{ \begin{array} { l } X = x - 1\\ Y = y + 5\\ \end{array} . {X=x−1Y=y+5​. 则有 d Y d X = X + Y X − Y \frac{dY}{dX} = \frac{X+Y}{X-Y} dXdY​=X−YX+Y​

令 U = Y X U = \frac{Y}{X} U=XY​,两边对x求导，有 d y d x = d u d x x + u \frac{dy}{dx} = \frac{du}{dx}x + u dxdy​=dxdu​x+u，代入上式可得 d u d x x + u = x + u x x − u x \frac{du}{dx}x+u = \frac{x+ux}{x-ux} dxdu​x+u=x−uxx+ux​,整理得 1 − u 1 + u 2 d u = 1 X d X \frac{1-u}{1+u^2}du = \frac{1}{X}dX 1+u21−u​du=X1​dX

两边同时积分，有 ∫ 1 d u 1 + u 2 − ∫ 1 / 2 ∗ d u 2 1 + u 2 = l n ∣ X ∣ + c \int \frac{1du}{1+u^2}-\int{\frac{1/2*du^2}{1+u^2}} = ln|X|+c ∫1+u21du​−∫1+u21/2∗du2​=ln∣X∣+c, 解得 arctan ⁡ u − 1 2 ln ⁡ ( 1 + u 2 ) = ln ⁡ ∣ X ∣ + C \arctan u - \frac{1}{2} \ln(1+u^2) = \ln |X| + C arctanu−21​ln(1+u2)=ln∣X∣+C

即 $\arctan ( \frac { y + 5 } { x - 1 } ) - \frac { 1 } { 2 } \ln \bigg[1 + ( \frac { y + 5 } { x - 1 } ) ^ { 2 }\bigg] = \ln {| x - 1 |} + C $ C为任意常数

定义（即x，y同时乘相同的倍数，等式仍成立） d y d x = f ( x , y ) = g ( y x ) , 称 d y d x = f ( x , y ) = f ( t x , t y ) 为 齐 次 微 分 方 程 \frac { dy } { dx } = {f ( x , y )} = g ( \frac { y } { x } ) , 称\frac { dy } { dx } = {f ( x , y )} = {f(tx,ty)}为齐次微分方程 dxdy​=f(x,y)=g(xy​),称dxdy​=f(x,y)=f(tx,ty)为齐次微分方程 解法 (y=ux ) [注意 u是关于x的函数] u = y x , 原 方 程 d y d x = f ( x , y ) = g ( u ) , u = y x , 则 d y d x = u + x d u d x 代 人 原 方 程 得 u + x d u d x = g ( u ) , 于 是 有 ∫ d u g ( u ) − u = ∫ d x x + C u=\frac{y}{x},原方程\frac{dy}{dx}=f(x,y)=g(u),u = \frac { y } { x } ,则 \frac { dy } { dx } = u + x\frac { du } { dx } \\ 代人原方程得 u + x\frac { du } { dx } = g ( u ), 于是有 \int \frac { du } { g ( u ) - u } = \int \frac { dx } { x } + C u=xy​,原方程dxdy​=f(x,y)=g(u),u=xy​,则dxdy​=u+xdxdu​代人原方程得u+xdxdu​=g(u),于是有∫g(u)−udu​=∫xdx​+C

定义

​ 形如 d y d x + P ( x ) y = 0 \frac { dy } { dx } + P ( x ) y = 0 dxdy​+P(x)y=0 的方程称为一阶齐次线性微分方程.

通解公式

​ y = C e − ∫ p ( x ) d x ( C 为 任 意 常 数 ) y = Ce^{-\int p(x)dx} \quad (C为任意常数) y=Ce−∫p(x)dx(C为任意常数)

推导 d y y = − P ( x ) d x   − > l n ∣ y ∣ = − ∫ P ( x ) d x + C 令 e c 0 = C ,   则 c ∈ ( 0 , + ∞ ) , ∣ y ∣ = e c 0 ∗ e − ∫ p ( x ) d x y = C e − ∫ p ( x ) d x   ( 易 知 y = 0 为 方 程 的 解 , C 为 任 意 常 数 ) \frac{dy}{y} = -P(x)dx \ -> ln|y| = -\int P(x)dx + C \\ 令e^{c_0} = C, \ 则 c\in(0,+∞) ,|y| = e^{c_0} * e^{-\int p(x)dx}\\ y = Ce^{-\int p(x)dx} \ (易知y = 0 为方程的解,C为任意常数) ydy​=−P(x)dx −>ln∣y∣=−∫P(x)dx+C令ec0​=C, 则c∈(0,+∞),∣y∣=ec0​∗e−∫p(x)dxy=Ce−∫p(x)dx (易知y=0为方程的解,C为任意常数)

定义

形如 d y d x + P ( x ) y = Q ( x ) \frac { dy } { dx } + P ( x ) y = Q ( x ) dxdy​+P(x)y=Q(x) 的方程称为一阶非齐次线性微分方程。[Q(x)!=0]

通解公式

​ y = [ ∫ Q ( x ) e ∫ p ( x ) d x d x + C ] e − ∫ P ( x ) d x y = \bigg[ \int Q(x)e^{\int p(x)dx} dx +C \bigg] e^{- \int P(x)dx} y=[∫Q(x)e∫p(x)dxdx+C]e−∫P(x)dx

推导 常数变易法（把c看出是x的函数c(x)） y = c ( x ) e − ∫ p ( x ) d x d y d x = c ′ ( x ) e − ∫ P ( x ) d x + ( − P ( x ) ) ∗ c ( x ) e − ∫ P ( x ) d x 把 y 和 上 式 代 入 d y d x + P ( x ) y = Q ( x ) c ′ ( x ) e − ∫ p ( x ) d x = Q ( x ) c ( x ) = ∫ Q ( x ) e ∫ p ( x ) d x + C 得 y = [ ∫ Q ( x ) e ∫ p ( x ) d x d x + C ] e − ∫ P ( x ) d x \begin{aligned} & y = c(x)e^{- \int p(x)dx} \\ & \frac{dy}{dx} = c'(x)e^{- \int P(x)dx}+(-P(x))*c(x)e^{-\int P(x)dx} \\ & 把y和上式代入\frac{dy}{dx}+P(x)y=Q(x)\\ & c'(x)e^{- \int p(x)dx} = Q(x) \\ & c(x) = \int Q(x)e^{\int p(x)dx} + C \\ & 得 \quad y = \bigg[ \int Q(x)e^{\int p(x)dx}dx +C \bigg] e^{- \int P(x)dx} \end{aligned} ​y=c(x)e−∫p(x)dxdxdy​=c′(x)e−∫P(x)dx+(−P(x))∗c(x)e−∫P(x)dx把y和上式代入dxdy​+P(x)y=Q(x)c′(x)e−∫p(x)dx=Q(x)c(x)=∫Q(x)e∫p(x)dx+C得y=[∫Q(x)e∫p(x)dxdx+C]e−∫P(x)dx​

例题 （公式法 或 变量变换）

【例】 求微分方程 x d y + ( x − 2 y ) d x = 0 xdy + ( x - 2y ) dx = 0 xdy+(x−2y)dx=0的通解.

【解】 x = 0 x = 0 x=0时, y = 0 y = 0 y=0,下面讨论 x ≠ 0 x \neq 0 x​=0时:

法一：由 x d y + ( x − 2 y ) d x = 0 xdy + ( x - 2y ) dx = 0 xdy+(x−2y)dx=0得 d y d x = 2 y − x x \frac { dy } { dx } = \frac { 2y - x } { x } dxdy​=x2y−x​或 d y d x − 2 x y = − 1 \frac { dy } { dx } - \frac { 2 } { x } y = -1 dxdy​−x2​y=−1,

解得 y = [ ∫ ( − 1 ) e ∫ − 2 x d x + c ] e − ∫ − 2 x d x = C x 2 + x y = [ \int ( - 1 ) e ^ {\int - \frac { 2 } { x } } dx + c ] e ^ { - \int - \frac { 2 } { x } dx} = Cx^2+x y=[∫(−1)e∫−x2​dx+c]e−∫−x2​dx=Cx2+x

法二：由 x d y + ( x − 2 y ) d x = 0 xdy + ( x - 2y ) dx = 0 xdy+(x−2y)dx=0,得 d y d x = 2 y x − 1 \frac { dy } { dx } = 2 \frac { y } { x } - 1 dxdy​=2xy​−1

令 y x = u \frac { y } { x } = u xy​=u,得 x d u d x = u − 1 x \frac { du } { dx } = u - 1 xdxdu​=u−1,变量分离得 d u u − 1 = d x x \frac { du } { u - 1 } = \frac { dx } { x } u−1du​=xdx​,

两边积分得 ln ⁡ ( u − 1 ) = ln ⁡ x + ln ⁡ C \ln ( u - 1 ) = \ln x + \ln C ln(u−1)=lnx+lnC,即 u − 1 = C x u - 1 = Cx u−1=Cx

故原方程通解为 y = C x 2 + x y = Cx ^ { 2 } + x y=Cx2+x

形如 d y d x + P ( x ) y = Q ( x ) y n ( n ≠ 0 , 1 ) \frac { dy } { dx } + P ( x ) y = Q ( x ) y ^ { n } ( n \neq 0 , 1 ) dxdy​+P(x)y=Q(x)yn(n​=0,1)的方程称为伯努利方程

引人变量变换 z = y 1 − n z=y^{1-n} z=y1−n，从而有 d z d x = ( 1 − n ) y − n d y d x \frac{dz}{dx}=(1- n)y^{-n}\frac{dy}{dx} dxdz​=(1−n)y−ndxdy​,代人原方程得 d z d x + ( 1 − n ) P ( x ) z = ( 1 − n ) Q ( x ) \frac { dz } { dx } + ( 1 - n ) P ( x ) z = ( 1 - n ) Q ( x ) dxdz​+(1−n)P(x)z=(1−n)Q(x),求解该一阶非齐次线性微分方程即可

【例】求方程 d y d x = 6 y x − x y 2 \frac { dy } { dx } = 6 \frac { y } { x } - xy ^ { 2 } dxdy​=6xy​−xy2的通解.

【解】 这是 n = 2 n = 2 n=2时的伯努利微分方程.

令 z = y − 1 z = y ^ { - 1 } z=y−1，得 d z d x = − y − 2 d y d x \frac { dz } { dx } = -y ^ { - 2 } \frac{dy}{dx} dxdz​=−y−2dxdy​ 代人原方程得 d z d x + 6 x z = x \frac { dz } { dx } + \frac { 6 } { x } z = x dxdz​+x6​z=x

这是线性微分方程,求得它的通解为 z = c x 6 + x 2 8 z = \frac { c } { x^6 } + \frac { x ^ { 2 } } { 8 } z=x6c​+8x2​

代回原来的变量 y y y得到 1 y = c x 6 + x 2 8 \frac { 1 } { y } = \frac { c } { x^6 } + \frac { x ^ { 2 } } { 8 } y1​=x6c​+8x2​或 x 6 y − x 8 8 = c \frac { x^6 } { y } - \frac { x ^ { 8 } } { 8 } = c yx6​−8x8​=c

这就是原方程的通解。此外，方程还有解 y = 0 y = 0 y=0

全微分 类似二型曲线积分，积分与路径无关

定义

​ 设 P ( x , y ) d x + Q ( x , y ) d y = 0 P ( x , y ) dx + Q ( x , y ) dy = 0 P(x,y)dx+Q(x,y)dy=0 满足 ∂ Q ∂ x = ∂ P ∂ y \frac { \partial Q } { \partial x } = \frac { \partial P } { \partial y } ∂x∂Q​=∂y∂P​ 则称 P ( x , y ) d x + Q ( x , y ) d y = 0 P ( x , y ) dx + Q ( x , y ) dy = 0 P(x,y)dx+Q(x,y)dy=0为全微分方程,通解为 u ( x , y ) = c u(x,y)=c u(x,y)=c

必要条件推导 ∂ 2 u ∂ y ∂ x = ∂ M ∂ y , ∂ 2 u ∂ x ∂ y = ∂ N ∂ x  由于  ∂ M ∂ y , ∂ N ∂ x  的连续性, 可得  ∂ 2 u ∂ y ∂ x = ∂ 2 u ∂ x ∂ y  故  ∂ M ∂ y = ∂ N ∂ x \begin{aligned} & \frac{\partial^{2} u}{\partial y \partial x} =\frac{\partial M}{\partial y}, \quad \frac{\partial^{2} u}{\partial x \partial y}=\frac{\partial N}{\partial x} \\ & \text { 由于 } \frac{\partial M}{\partial y}, \frac{\partial N}{\partial x} \text { 的连续性, 可得 } \frac{\partial^{2} u}{\partial y \partial x}=\frac{\partial^{2} u}{\partial x \partial y} \\ & \text { 故 } \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x} \end{aligned} ​∂y∂x∂2u​=∂y∂M​,∂x∂y∂2u​=∂x∂N​ 由于 ∂y∂M​,∂x∂N​ 的连续性, 可得 ∂y∂x∂2u​=∂x∂y∂2u​ 故 ∂y∂M​=∂x∂N​​

普通解法

判断是否满足必要条件—对x积分得到φ(y)，为确定φ(y)把积分后的式子代入对y求偏导的等式，并使得它成立，即为解

例题

分项组合法

例题

简单二元函数的全微分 y   d x + x   d y = d ( x y ) y   d x − x   d y y 2 = d ( x y ) − y   d x + x   d y x 2 = d ( y x ) y   d x − x   d y x y = d ( ln ⁡ ∣ x y ∣ ) y   d x − x   d y x 2 + y 2 = d ( arctan ⁡ x y ) y   d x − x   d y x 2 − y 2 = 1 2   d ( ln ⁡ ∣ x − y x + y ∣ ) \begin{array}{l} y \mathrm{~d} x+x \mathrm{~d} y=\mathrm{d}(x y) \\ \frac{y \mathrm{~d} x-x \mathrm{~d} y}{y^{2}}=\mathrm{d}\left(\frac{x}{y}\right) \\ \frac{-y \mathrm{~d} x+x \mathrm{~d} y}{x^{2}}=\mathrm{d}\left(\frac{y}{x}\right) \\ \frac{y \mathrm{~d} x-x \mathrm{~d} y}{x y}=\mathrm{d}\left(\ln \left|\frac{x}{y}\right|\right) \\ \frac{y \mathrm{~d} x-x \mathrm{~d} y}{x^{2}+y^{2}}=\mathrm{d}\left(\arctan \frac{x}{y}\right) \\ \frac{y \mathrm{~d} x-x \mathrm{~d} y}{x^{2}-y^{2}}=\frac{1}{2} \mathrm{~d}\left(\ln \left|\frac{x-y}{x+y}\right|\right) \end{array} y dx+x dy=d(xy)y2y dx−x dy​=d(yx​)x2−y dx+x dy​=d(xy​)xyy dx−x dy​=d(ln∣∣∣​yx​∣∣∣​)x2+y2y dx−x dy​=d(arctanyx​)x2−y2y dx−x dy​=21​ d(ln∣∣∣​x+yx−y​∣∣∣​)​

思想：找一个连续可微函数u，使得 uMdx+uNdy = 0 为一恰微分方程，从而把问题转换为解恰当微分方程

​ 存在连续函数μ!=0，使得 μ ( x , y ) M ( x , y ) d x + μ ( x , y ) N ( x , y ) d y = 0 \mu ( x , y ) M ( x , y ) dx + \mu ( x , y ) N ( x , y ) dy = 0 μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0为一恰当方程，则μ(x,y)称为原方程Mdx+Ndy=0的积分因子

充要条件 ∂ ( μ M ) ∂ y = ∂ ( μ N ) ∂ x \frac { \partial ( \mu M ) } { \partial y } = \frac { \partial ( \mu N ) } { \partial x } ∂y∂(μM)​=∂x∂(μN)​ 求积分因子

仅与y有关 ( ∂ M ∂ y − ∂ N ∂ x ) / ( − M ) = φ ( y ) (\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x})/(-M)=\varphi(y) (∂y∂M​−∂x∂N​)/(−M)=φ(y) 则积分因子为 μ = e ∫ φ ( y ) d y \mu=\mathrm{e}^{\int \varphi(y) d y} μ=e∫φ(y)dy

或仅对x有关 ( ∂ M ∂ y − ∂ N ∂ x ) / ( N ) = ψ ( x ) (\frac{\partial M}{\partial y}-{\frac{\partial N}{\partial x}})/(N)=\psi(x) (∂y∂M​−∂x∂N​)/(N)=ψ(x) ,则积分因子为 μ = e ∫ ψ ( x ) d x \mu=\mathrm{e}^{\int \psi(x) d x} μ=e∫ψ(x)dx

计算出适合的u，然后改写原方程为一恰当微分方程，使用恰当微分方程解法解决即可。

例题

仅有n次导 y(n) = f(x)

解法：进行n次不定积分求解即可

f(x,y’,y’’)

解法(转换为一阶微分方程)

 令  y ′ = d y   d x = p , 则  y ′ ′ = d p   d x , 原方程化为  f ( x , p , d p   d x ) = 0 ;   解出  p = φ ( x , C 1 ) , 则原方程通解为  y = ∫ φ ( x , C 1 ) d x + C 2 .  \begin{array}{l}\text { 令 } y^{\prime}=\frac{\mathrm{d} y}{\mathrm{~d} x}=p \text {, 则 } y^{\prime \prime}=\frac{\mathrm{d} p}{\mathrm{~d} x} \text {, 原方程化为 } f\left(x, p, \frac{\mathrm{d} p}{\mathrm{~d} x}\right)=0 \text {; } \\ \text { 解出 } p=\varphi\left(x, C_{1}\right) \text {, 则原方程通解为 } y=\int \varphi\left(x, C_{1}\right) \mathrm{d} x+C_{2} \text {. }\end{array}  令 y′= dxdy​=p, 则 y′′= dxdp​, 原方程化为 f(x,p, dxdp​)=0;  解出 p=φ(x,C1​), 则原方程通解为 y=∫φ(x,C1​)dx+C2​. ​

【例】求微分方程$ y ^ { \prime \prime } + 2xy’ ^ { 2 } = 0 满 足 初 始 条 件 满足初始条件 满足初始条件 y ( 0 ) = 1 , y ^ { \prime } ( 0 ) = - \frac { 1 } { 2 }$的特解。

【解】 令 y ′ = p , 则 y ′ ′ = d p d x , 代 入 得 d p d x + 2 x p 2 = 0 令y' = p,则y'' = \frac{dp}{dx},代入得 \frac{dp}{dx} + 2xp^2=0 令y′=p,则y′′=dxdp​,代入得dxdp​+2xp2=0

变 量 分 离 得 1 p 2 d p = − 2 x d x , 两 边 积 分 得 1 p = x 2 + c 1 变量分离得\frac{1}{p^2}dp = -2xdx,两边积分得 \frac{1}{p} = x^2+c_1 变量分离得p21​dp=−2xdx,两边积分得p1​=x2+c1​

把 y ′ ( 0 ) = − 1 2 = p 代 入 得 C 1 = − 2 , d y d x = 1 x 2 − 2 , 积 分 得 y = 1 2 2 ln ⁡ ∣ x − 2 x + 2 ∣ + c 2 把y'(0) = -\frac{1}{2}=p 代入得 C_1=-2 ,\frac{dy}{dx} = \frac{1}{x^2-2},积分得 y = \frac { 1 } { 2 \sqrt { 2 } } \ln |\frac { x - \sqrt { 2 } } { x + \sqrt { 2 } } | + c _ { 2 } 把y′(0)=−21​=p代入得C1​=−2,dxdy​=x2−21​,积分得y=22 ​1​ln∣x+2 ​x−2 ​​∣+c2​

把 y ( 0 ) = 1 代 入 得 C 2 = 1 , 原 方 程 的 满 足 初 始 条 件 的 特 解 为 y = 1 2 2 ln ⁡ ∣ x − 2 x + 2 ∣ + 1 把y(0)=1代入得C_2=1, 原方程的满足初始条件的特解为 y = \frac { 1 } { 2 \sqrt { 2 } } \ln |\frac { x - \sqrt { 2 } } { x + \sqrt { 2 } |} + 1 把y(0)=1代入得C2​=1,原方程的满足初始条件的特解为y=22 ​1​ln∣x+2 ​∣x−2 ​​+1

f(y,y’,y’’) 解法(转化为一阶)

 令  y ′ = p , p d y = 1 d x , d x = d y p  , 则  y ′ ′ = d p   d x = p d p   d y , 原方程化为  f ( y , p , p d p   d y ) = 0 ;   解出  p = φ ( y , C 1 )  或  d y φ ( y , C 1 ) = d x , 两边积分得  ∫ d y φ ( y , C 1 ) = x + C 2 , 进而求出原方  \begin{array}{l}\text { 令 } y^{\prime}=p, \frac{p}{dy}=\frac{1}{dx},dx = \frac{dy}{p} \ \text {, 则 } y^{\prime \prime}=\frac{\mathrm{d} p}{\mathrm{~d} x}=p \frac{\mathrm{d} p}{\mathrm{~d} y} \text {, 原方程化为 } f\left(y, p, p \frac{\mathrm{d} p}{\mathrm{~d} y}\right)=0 \text {; } \\ \text { 解出 } p=\varphi\left(y, C_{1}\right) \text { 或 } \frac{\mathrm{d} y}{\varphi\left(y, C_{1}\right)}=\mathrm{d} x \text {, 两边积分得 } \int \frac{\mathrm{d} y}{\varphi\left(y, C_{1}\right)}=x+C_{2} \text {, 进而求出原方 }\end{array}  令 y′=p,dyp​=dx1​,dx=pdy​ , 则 y′′= dxdp​=p dydp​, 原方程化为 f(y,p,p dydp​)=0;  解出 p=φ(y,C1​) 或 φ(y,C1​)dy​=dx, 两边积分得 ∫φ(y,C1​)dy​=x+C2​, 进而求出原方 ​

【例】求 y y ′ ′ = y ′ 2 yy ^ { \prime \prime } = y ^ { \prime 2 } yy′′=y′2满足初始条件 y ( 0 ) = y ′ ( 0 ) = 1 y ( 0 ) = y ^ { \prime } ( 0 ) = 1 y(0)=y′(0)=1的特解.

【解】令y’ = p,则 d y d x = p , d x = d y p , 得 y ′ ′ = d p d x = p d p d y \frac{dy}{dx} = p,dx = \frac{dy}{p},得y'' = \frac{dp}{dx} = p\frac{dp}{dy} dxdy​=p,dx=pdy​,得y′′=dxdp​=pdydp​

代 入 原 方 程 得 y p d p d y − p 2 = 0 , 解 得 p = c 1 y 代入原方程得 yp\frac{dp}{dy}-p^2 = 0,解得p=c_1y 代入原方程得ypdydp​−p2=0,解得p=c1​y

根 据 y ( 0 ) = 1 = y ′ ( 0 ) 代 入 得 ， 1 = c 1 , 可 得 d y d x − y = 0 , 解 得 y = c 2 e x 根据 y(0)=1=y'(0) 代入得，1=c_1,可得\frac{dy}{dx}-y=0,解得y=c_2e^x 根据y(0)=1=y′(0)代入得，1=c1​,可得dxdy​−y=0,解得y=c2​ex

把 y ( 0 ) = 1 代 入 得 1 = c 2 , 故 y = e x 把y(0)=1代入得1=c_2 ,故y=e^x 把y(0)=1代入得1=c2​,故y=ex

除上面两种类型外，还可能是缺y’，此时可令p=y’'

常微分方程 p120 第四章

n阶齐次线性微分方程 定义 y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x ) y ′ + a n ( x ) y = 0 ( 1 ) y ^ { ( n ) } + a _ { 1 } ( x ) y ^ { ( n - 1 ) } + \cdots + a _ { n - 1 } ( x ) y ^ { \prime } + a _ { n } ( x ) y = 0 \quad (1) y(n)+a1​(x)y(n−1)+⋯+an−1​(x)y′+an​(x)y=0(1)

n阶非齐次线性微分方程 定义 y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x y ) ′ + a n ( x ) y = f ( x ) ( 2 ) y ^ { ( n ) } + a _ { 1 } ( x ) y ^ { ( n - 1 ) } + \dots + a _ { n - 1 } ( xy ) ^ { \prime } + a _ { n } ( x ) y = {f ( x )} \quad (2) y(n)+a1​(x)y(n−1)+⋯+an−1​(xy)′+an​(x)y=f(x)(2)

分解 若 f ( x ) = f 1 ( x ) + f 2 ( x ) , 则 ( 2 ) 可 分 解 为 如 下 两 个 方 程 : y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x ) y ′ + a n ( x ) y = f 1 ( x ) ( 2.1 ) y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x y ) ′ + a n ( x ) y = f 2 ( x ) ( 2.2 ) 若{f ( x )} = f _ { 1 } ( x ) + f _ { 2 } ( x ),则(2)可分解为如下两个方程: \\ y ^ { ( n ) } + a _ { 1 } ( x ) y ^ { ( n - 1 ) } + \dots + a _ { n - 1 } ( x ) y ^ { \prime } + a _ { n } ( x ) y = f _ { 1 } ( x ) \quad (2.1) \\ y ^ { ( n ) } + a _ { 1 } ( x ) y ^ { ( n - 1 ) } + \dots + a _ { n - 1 } ( xy ) ^ { \prime } + a _ { n } ( x ) y = f _ { 2 } ( x ) \quad (2.2) 若f(x)=f1​(x)+f2​(x),则(2)可分解为如下两个方程:y(n)+a1​(x)y(n−1)+⋯+an−1​(x)y′+an​(x)y=f1​(x)(2.1)y(n)+a1​(x)y(n−1)+⋯+an−1​(xy)′+an​(x)y=f2​(x)(2.2) 解的结构

实值解与复值解 （常微分方程第三版 p136）

设 y = e λ x ,   λ 可 实 可 复 y = e^{\lambda x} ,\ \lambda可实可复 y=eλx, λ可实可复，复值解如下 e ( α + i β ) = e a ( cos ⁡ β t + i sin ⁡ β t ) e ( α − i β ) = e a ( cos ⁡ β t − i sin ⁡ β t ) e ^ { ( \alpha + i\beta ) } = e ^ { a } ( \cos \beta t + i \sin \beta t ) \\ e ^ { ( \alpha - i\beta ) } = e ^ { a } ( \cos \beta t - i \sin \beta t ) e(α+iβ)=ea(cosβt+isinβt)e(α−iβ)=ea(cosβt−isinβt) 实部和虚部和共轭复值函数也是方程的解，一对共轭复根对应的两个实值解如下

λ = α ± i β e a x cos ⁡ β t e a x sin ⁡ β t \lambda = \alpha \pm i \beta \\ e ^ { ax } \cos \beta t \quad e ^ { ax } \sin \beta t λ=α±iβeaxcosβteaxsinβt

以二阶常系数为例（3种情形）

$ 二阶常系数线性齐次微分方程的一般形式为y ^ { \prime \prime } + py ^ { \prime } + qy = 0, \ 其特征方程为r ^ { 2 } + pr + q = 0, \ 设r _ { 1 } , r _ { 2 }为该方程的两个根.$

n阶常系数 （以三阶为例，根据特征根的重数确定x的次数）

$ 特征方程为\lambda ^ { 3 } + p \lambda ^ { 2 } + q \lambda + r = 0,根据特征值\lambda _ { 1 } , \lambda _ { 2 } , \lambda _ { 3 }的不同情形通解如下:$ ( 1 ) λ 1 , λ 2 , λ 3 ∈ R 且 它 们 两 两 互 不 等 , 则 通 解 为 y = C 1 e λ 1 x + C 2 e λ 2 x + C 3 e λ 3 x ； ( 2 ) λ 1 , λ 2 , λ 3 ∈ R 且 λ 1 = λ 2 ≠ λ 3 , 则 通 解 为 y = ( C 1 + C 2 x ) e λ 1 x + C 3 e λ 3 x ; ( 3 ) λ 1 , λ 2 , λ 3 ∈ R 且 λ 1 = λ 2 = λ 3 , 则 通 解 为 y = ( C 1 + C 2 x + C 3 x 2 ) e λ 1 x ( 4 ) λ 1 ∈ R , λ 2 , 3 = α ± β i ( β ≠ 0 ) ,   则 通 解 为 y = C 1 e λ 1 x + e α x ( C 2 cos ⁡ β x + C 3 sin ⁡ β x ) \begin{aligned} & (1)\lambda _ { 1 } , \lambda _ { 2 } , \lambda _ { 3 } \in \mathbf { R }且它们两两互不等,则通解为y = C _ { 1 } e ^ { \lambda _ 1 x } + C _ { 2 } e ^ { \lambda _2x } + C _ { 3 } e ^ { \lambda _ 3x }； \\ & (2)\lambda _ { 1 } , \lambda _ { 2 } , \lambda _ { 3 } \in \mathbf { R }且\lambda _ { 1 } = \lambda _ { 2 } \neq \lambda _ { 3 },则通解为y = ( C _ { 1 } + C _ { 2 } x ) e ^ { \lambda _ 1 x } + C _ { 3 } e ^ { \lambda _ 3 x }; \\ & (3)\lambda _ { 1 } , \lambda _ { 2 } , \lambda _ { 3 } \in \mathbf { R }且 { \lambda _ { 1 } = \lambda _ { 2 } = \lambda _ { 3 } },则通解为y = ( C _ { 1 } + C _ { 2 } x + C _ { 3 } x ^ { 2 } ) e ^ { \lambda _ 1 x } \\ & (4)\lambda _ { 1 } \in R ,\lambda _ { 2,3 } = \alpha \pm \beta i ( \beta \neq 0 ),\ 则通解为y = C _ { 1 } e ^ { \lambda _ 1 x } + e ^ { \alpha x } ( C _ 2 \cos \beta x + C _ 3 \sin \beta x ) \end{aligned} ​(1)λ1​,λ2​,λ3​∈R且它们两两互不等,则通解为y=C1​eλ1​x+C2​eλ2​x+C3​eλ3​x；(2)λ1​,λ2​,λ3​∈R且λ1​=λ2​​=λ3​,则通解为y=(C1​+C2​x)eλ1​x+C3​eλ3​x;(3)λ1​,λ2​,λ3​∈R且λ1​=λ2​=λ3​,则通解为y=(C1​+C2​x+C3​x2)eλ1​x(4)λ1​∈R,λ2,3​=α±βi(β​=0), 则通解为y=C1​eλ1​x+eαx(C2​cosβx+C3​sinβx)​ （重数k-1=x的最高次数）

二阶非齐线性（等式右边不为0）两种情形：普通型，带三角函数型

求解步骤: （齐次通解+特解 == 非齐通解）

(1)求出对应齐次线性微分方程 y ′ ′ + p y ′ + q y = 0 y ^ { \prime \prime } + py ^ { \prime } + qy = 0 y′′+py′+qy=0的通解 Y = ∑ i = 1 2 c i e λ i ( cos ⁡ β x + sin ⁡ β x ) Y=\sum_{i=1}^{2}c_ie^{\lambda_i}(\cos \beta x + \sin \beta x) Y=∑i=12​ci​eλi​(cosβx+sinβx)

(2)用待定系数法求出非齐次线性微分方程 y ′ ′ + p y ′ + q y = f ( x ) y ^ { \prime \prime } + py ^ { \prime } + qy = {f ( x )} y′′+py′+qy=f(x)的一个特解 y ∗ y* y∗.

①当 f ( x ) = Q ( x ) e x t {f ( x )} = Q ( x ) e ^ { xt } f(x)=Q(x)ext时,设特解 y ∗ = x k P ( x ) e λ x y* = x ^ { k } P ( x ) e ^ { \lambda { x } } y∗=xkP(x)eλx,其中按 λ \lambda λ不是 r 2 + p r + q = 0 r ^ { 2 } + pr + q = 0 r2+pr+q=0的根、是单根、是二重根时， k k k分别取0.1.2.

【说明】 P ( x ) P ( x ) P(x)是与 Q ( x ) Q ( x ) Q(x)次数相同的多项式，将 y ∗ y* y∗代入非齐次方程，比较两端，求出 P ( x ) P ( x ) P(x),便可得特解 y ∗ y* y∗

②当 f ( x ) = e λ x [ P l ( x ) cos ⁡ w x + Q n ( x ) sin ⁡ w x ] {f ( x )} = e ^ { \lambda x } [ P _ { l } ( x ) \cos wx + Q _ { n } ( x ) \sin wx ] f(x)=eλx[Pl​(x)coswx+Qn​(x)sinwx]时,设特解 y ∗ = x k e λ x [ R m ( 1 ) ( x ) cos ⁡ w x + R m ( 2 ) ( x ) sin ⁡ w x ] y* = x ^ { k } e ^ { \lambda x } [ R _ { m } ^ { (1) } ( x ) \cos wx + R _ { m } ^ { (2) } ( x ) \sin wx ] y∗=xkeλx[Rm(1)​(x)coswx+Rm(2)​(x)sinwx]

其中按 λ ± i w \lambda \pm iw λ±iw不是 r 2 + p r + q = 0 r ^ { 2 } + pr + q = 0 r2+pr+q=0的根、是特征根、k分别取0，1。 R m ( 1 ) ( x ) R _ { m } ^ { ( 1 ) } ( x ) Rm(1)​(x)与 R m ( 2 ) ( x ) R _ { m } ^ { (2) } ( x ) Rm(2)​(x)是 m m m次多项式，但其系数不同， m = m a x { l , n } m = max \{ l , n \} m=max{l,n} 【说明】将 y y y代入非齐次方程,比较两端，求出 R m ( 1 ) ( x ) R _ { m } ^ { (1) } ( x ) Rm(1)​(x)与 R m ( 2 ) ( x ) R _ { m } ^ { (2) } ( x ) Rm(2)​(x),便可以求得特解 y ∗ y* y∗.

(3)通解为 y = Y + y ∗ y = Y + y* y=Y+y∗.

f(x)为普通型 f ( x ) = P n ( x ) e k x {f ( x )} = P _ { n } ( x ) e ^ { kx } f(x)=Pn​(x)ekx

技巧（待补充）：代入原方程整理后的式子为: Q ′ ′ + ( 2 k + p ) Q ′ + ( k 2 + p k + q ) Q = P n ( x ) . Q'' + (2k + p)Q' + (k^2+pk+q)Q = P _ { n } ( x ) . Q′′+(2k+p)Q′+(k2+pk+q)Q=Pn​(x).·特别地,若k与一个特征值相同,则 Q r ′ + ( 2 k + p ) Q ′ = P n ( x ) Q ^ { r \prime } + ( 2k + p ) Q ^ { \prime } = P _ { n } ( x ) Qr′+(2k+p)Q′=Pn​(x)若k与两个特征值相同,则 Q ′ ′ = P n ( x ) Q ^ { \prime \prime } = P _ { n } ( x ) Q′′=Pn​(x)

f(x)为三角形式 f ( x ) = e a x [ P l ( x ) cos ⁡ β x + P n ( x ) sin ⁡ β x ] {f ( x )} = e ^ { ax } [ P _ { l } ( x ) \cos \beta x + P _ { n } ( x ) \sin \beta x ] f(x)=eax[Pl​(x)cosβx+Pn​(x)sinβx]，其中 P 1 ( x ) , P n ( x ) P _ { 1 } ( x ) , P _ { n } ( x ) P1​(x),Pn​(x)分别为 x x x的 l l l次 n n n次多项式 特解设为： y ′ = x k e a x [ R m ( 1 ) ( x ) cos ⁡ β x + R m ( 2 ) ( x ) sin ⁡ β x ] y ^ { \prime } = x ^ { k } e ^ { ax } [ R _ {m} ^ { (1) } ( x ) \cos \beta x + R _ { m } ^ { (2) } ( x ) \sin \beta x ] y′=xkeax[Rm(1)​(x)cosβx+Rm(2)​(x)sinβx]，其中 R m ( 1 ) ( x ) , R ( 2 ) ( x ) R _ { m } ^ { ( 1 ) } ( x ) , R ^ { ( 2 ) } ( x ) Rm(1)​(x),R(2)(x)是两个 m m m次多项式: m = m a x { l , n } m = max \{ l , n \} m=max{l,n}

【例】设 x = x ( y ) x = x ( y ) x=x(y)可导, x ′ ( y ) ≠ 0 x ^ { \prime } ( y ) \neq 0 x′(y)​=0且满足方程 d 2 x d y 2 + ( y + sin ⁡ x ) ( d x d y ) 3 = 0 \frac { d ^ { 2 } x } { dy ^ { 2 } } + ( y + \sin x ) ( \frac { dx } { dy } ) ^ { 3 } = 0 dy2d2x​+(y+sinx)(dydx​)3=0 (1)将方程化为 y y y关于 x x x的方程; (2)求满足初始条件 y ( 0 ) = 0. y ′ ( 0 ) = 3 2 y ( 0 ) = 0.y ^ { \prime } ( 0 ) = \frac { 3 } { 2 } y(0)=0.y′(0)=23​的特解 y ( x ) y ( x ) y(x)

已知一个通解，求另外一个线性无关的通解

利普希茨

​ 存在常数L＞0，使得不等式 ∣ f ( x , y 1 ) − f ( x , y 2 ) ∣ ≤ L ∣ y 1 − y 2 ∣ | {f ( x , y _ { 1 } )} - {f ( x , y _ { 2 } )} | \leq L | y _ { 1 } - y _ { 2 } | ∣f(x,y1​)−f(x,y2​)∣≤L∣y1​−y2​∣ （称为y满足利普希茨条件）对于所有的(x,y1,)，(x,y2)∈R都成立，L称为利普希茨常数。

几何意义：利普希茨连续就是函数上任意两点连线的斜率是有界的。直觉上，利普希茨连续函数限制了函数改变的速度

Peano 定理 (皮亚诺存在性定理, 解的存在性定理)

​ 设函数 f(x,y) 在矩形区域R中连续，则初值问题 $\frac{dy}{dx} = f(x,y)，y_{x_0}=y_0 $ 在区间 [ R : ∣ x − x 0 ∣ ≤ a , ∣ y − y 0 ∣ ≤ b R:|x-x_0| \le a, |y-y_0| \le b R:∣x−x0​∣≤a,∣y−y0​∣≤b] 上至少有一个解。更进一步地，若满足利普希茨条件，则解存在且唯一。

定理一

​ 若f(x,y)在矩形域R上连续且关于y满足利普希茨条件，则一阶微分方程 d y d x = f ( x , y ) ， R : ∣ x − x 0 ∣ ≤ a , ∣ y − y 0 ∣ ≤ b \frac{dy}{dx} = f(x,y)，R:|x-x_0| \le a, |y-y_0| \le b dxdy​=f(x,y)，R:∣x−x0​∣≤a,∣y−y0​∣≤b 存在唯一解y=y(x)，定义于区间|x-x0|≤h上。

​ 有时候不好用利普希茨判断，常用 fy存在且连续代替。（P 85）

若f(x,y)连续则解存在，此时若fy不连续，则解存在但不唯一。

注意

例题1

例题2

例题3 （考察 解的存在性和唯一性的判断）

【解】

（Peano 定理）解的存在性： f ( x , y ) = y 1 / 3 f(x,y) = y^{1/3} f(x,y)=y1/3，在R上连续，因此解存在；

（利普希茨条件）解的唯一性： ∂ f / ∂ y = 1 3 y − 2 / 3 \partial f/ \partial y = \frac{1}{3}y^{-2/3} ∂f/∂y=31​y−2/3 在(0,0)无定义即不连续，则不满足利普希茨条件，因此解不唯一。

常微分方程的两个解 y = 0 , y = 2 3 ( x ) 3 2 y=0, y = \frac{2}{3}(x)^{\frac{3}{2}} y=0,y=32​(x)23​

对于G选项，显然在区域R内满足利普希茨条件，则解存在且唯一。解为 y = 2 3 ( x + 1 ) 3 2 y = \frac{2}{3}(x+1)^{\frac{3}{2}} y=32​(x+1)23​

无限个解，例如解的形式为 y = x + c y=x+c y=x+c,不论c如何变化都满足微分方程，则有无数个解

定理二

​ 若在点(x0，y0, y’0)的某一邻域中，

F ( x , y , y ′ ) {F ( x , y , y ^ { \prime } )} F(x,y,y′)对所有变元 ( x , y , y ′ ) ( x , y , y ^ { \prime } ) (x,y,y′)连续,且存在连续偏导数;

F ( x 0 , y 0 , y 0 ′ ) = 0 {F ( x _ { 0 } , y _ { 0 } , y _ { 0 } ^ { ' } )} = 0 F(x0​,y0​,y0′​)=0；

∂ F ( x 0 , y 0 , y 0 ’ ) ∂ y ′ ≠ 0 \frac { \partial{F ( x _ { 0 } , y _ { 0 }, y _ { 0 }’ )} } {\partial y'} \neq 0 ∂y′∂F(x0​,y0​,y0​’)​​=0

朗斯基行列式指的是:在区间 x ∈ ( a , b ) x \in ( a , b ) x∈(a,b)上有一组函数 y 1 ( x ) , y 2 ( x ) , … , y n ( x ) } y _ { 1 } ( x ) , y _ { 2 } ( x ) , \dots , y _ { n } ( x ) \} y1​(x),y2​(x),…,yn​(x)}且每个函数都具有n - 1阶导数,它们构成如下所示形式的行列式，称为朗斯基行列式，记为 W ( y ( x ) ) W ( y ( x ) ) W(y(x))或 W ( x ) W ( x ) W(x)。

定理

​ 若函数 y 1 ( x ) , y 2 ( x ) , … , y n ( x ) } y _ { 1 } ( x ) , y _ { 2 } ( x ) , \dots , y _ { n } ( x ) \} y1​(x),y2​(x),…,yn​(x)}在区间a≤x≤b上线性相关，则W(x)=0

【例1】微分方程 y ′ + sin ⁡ y + x cos ⁡ y + x = 0 y' + \sin y +x \cos y + x = 0 y′+siny+xcosy+x=0 求通解

解：由 y ′ + sin ⁡ y + x ( 1 + cos ⁡ y ) = 0 y ^ { \prime } + \sin y + x ( 1 + \cos y ) = 0 y′+siny+x(1+cosy)=0 得 y ′ + 2 sin ⁡ y 2 cos ⁡ y 2 + 2 x cos ⁡ 2 y 2 = 0 y ^ { \prime } + 2 \sin \frac { y } { 2 } \cos \frac { y } { 2 } + 2x \cos ^ { 2 } \frac { y } { 2 } = 0 y′+2sin2y​cos2y​+2xcos22y​=0

两边除以 2 cos ⁡ 2 y 2 2 \cos ^ { 2 } \frac { y } { 2 } 2cos22y​得 1 2 sec ⁡ 2 y 2 ⋅ d y d x + tan ⁡ y 2 = − x \frac { 1 } { 2 } \sec ^ {2} \frac { y } { 2 } \cdot \frac { dy } { dx } + \tan \frac { y } { 2 } = -x 21​sec22y​⋅dxdy​+tan2y​=−x或 d ( tan ⁡ y 2 ) d x + tan ⁡ y 2 = − x \frac { d( \tan \frac { y } { 2 } ) } { dx } + \tan \frac { y } { 2 } = -x dxd(tan2y​)​+tan2y​=−x

令 u = tan ⁡ y 2 u = \tan \frac { y } { 2 } u=tan2y​,原方程化为 d u d x + u = − x \frac { du } { dx } + u = -x dxdu​+u=−x，解得 u = [ ( − x ) e ∫ d x d x + c ] ⋅ e − ∫ d x = [ − ( x − 1 ) e x + C ] e − x u = [ ( - x ) e ^ { \int dx} dx + c ] \cdot e ^ { - \int dx } = [ - ( x - 1 ) e ^ { x } + C ] e ^ { - x } u=[(−x)e∫dxdx+c]⋅e−∫dx=[−(x−1)ex+C]e−x

原方程的通解为 tan ⁡ y 2 = C e − x + 1 − x \tan \frac { y } { 2 } = Ce ^ { - x } + 1 - x tan2y​=Ce−x+1−x

【例2】微分方程 y ′ = 1 2 x − y 2 y' = \frac{1}{2x-y^2} y′=2x−y21​ 的通解为_______

【解】原方程化为 d x d y = 2 x − y 2 \frac { dx } { dy } = 2x - y ^ { 2 } dydx​=2x−y2或 d x d y − 2 x = − y 2 \frac { dx } { dy } - 2x = -y ^ { 2 } dydx​−2x=−y2

解得 x = [ ∫ ( − y 2 ) e − 2 d y d y + c ] e − ∫ − 2 d y = [ ( − y 2 ) e − 2 y d y + c ] e 2 y x = [ \int ( - y ^ { 2 } ) e ^ { - 2 dy} dy + c ] e ^ { - \int -2 dy} = [ ( - y ^ { 2 }) e ^ { -2 y} dy +c] e ^ { 2y } x=[∫(−y2)e−2dydy+c]e−∫−2dy=[(−y2)e−2ydy+c]e2y,

故原方程的通解为 x = C e 2 y + y 2 2 + y 2 + 1 4 x = Ce ^ { 2y } + \frac { y ^ { 2 } } { 2 } + \frac { y } { 2 } + \frac { 1 } { 4 } x=Ce2y+2y2​+2y​+41​

伯努利

变量变换

【例】求微分方程 d y d x = 1 ( x + y ) 2 \frac { dy } { dx } = \frac { 1 } { ( x + y ) ^ { 2 } } dxdy​=(x+y)21​的通解.

【解】令 x + y = u x + y = u x+y=u,则 d y d x = d u d x − 1 \frac { dy } { dx } = \frac { du } { dx } - 1 dxdy​=dxdu​−1,代人原方程得 d u d x − 1 = 1 u 2 \frac { du } { dx } - 1 = \frac { 1 } { u ^ { 2 } } dxdu​−1=u21​,即 d u d x = 1 + u 2 u 2 \frac { du } { dx } = \frac { 1 + u ^ { 2 } } { u ^ { 2 } } dxdu​=u21+u2​

变量分离得 ( 1 − 1 1 + u 2 ) d x = d x ( 1 - \frac { 1 } { 1 + u ^ { 2 } } ) dx = dx (1−1+u21​)dx=dx

积分得 u − a r c tan ⁡ u = x + c u - arc \tan u = x + c u−arctanu=x+c,故通解 y − a r c tan ⁡ ( x + y ) = C y - arc \tan ( x + y ) = C y−arctan(x+y)=C

齐次

非齐次+组合型

【例】求微分方程 y ′ ′ + y = x + cos ⁡ x y ^ { \prime \prime } + y = x + \cos x y′′+y=x+cosx的通解

【解】特征方程为 λ 2 + 1 = 0 \lambda ^ { 2 } + 1 = 0 λ2+1=0,特征值为 λ 1 , 2 = ± i \lambda _ { 1 , 2 } = \pm i λ1,2​=±i

y ′ ′ + y = 0 y ^ { \prime \prime } + y = 0 y′′+y=0的通解为 y = C 1 cos ⁡ x + C 2 sin ⁡ x y = C _ { 1 } \cos x + C _ { 2 } \sin x y=C1​cosx+C2​sinx

令 y ′ ′ + y = x y ^ { \prime \prime } + y = x y′′+y=x ，显然有特解 y 1 ( x ) = x y _ { 1 } ( x ) = x y1​(x)=x

令 y ′ ′ + y = cos ⁡ x y ^ { \prime \prime } + y = \cos x y′′+y=cosx ，显然有特解为 y 2 ( x ) = x ( a cos ⁡ x + b sin ⁡ x ) y _ { 2 } ( x ) = x ( a \cos x + b \sin x ) y2​(x)=x(acosx+bsinx)

代入原方程得 a = 0 , b = 1 2 a = 0 , b = \frac { 1 } { 2 } a=0,b=21​

故原方程的通解为 y = C 1 cos ⁡ x + C 2 sin ⁡ x + x + 1 2 x sin ⁡ x y = C _ { 1 } \cos x + C _ { 2 } \sin x + x + \frac { 1 } { 2 } x \sin x y=C1​cosx+C2​sinx+x+21​xsinx

【例】求微分方程 y ′ ′ ′ = 3 x 2 1 + x 3 y ′ ′ y ^ { \prime \prime \prime} = \frac { 3x ^ { 2 } } { 1 + x ^ { 3 } } y ^ { \prime \prime} y′′′=1+x33x2​y′′满足初始条件 y ( 0 ) = 0 , y ′ ( 0 ) = 1 , y n ( 0 ) = 4 y ( 0 ) = 0 , y ^ { \prime } ( 0 ) = 1 , y ^ { n } ( 0 ) = 4 y(0)=0,y′(0)=1,yn(0)=4的特解。

【解】令y’’ = p, 则 d p p = 3 x 2 1 + x 3 , 得 p = C 1 ( 1 + x 3 ) \frac{dp}{p} = \frac{3x^2}{1+x^3},得p=C_1( 1 + x^3) pdp​=1+x33x2​,得p=C1​(1+x3)

∵ y ′ ′ ( 0 ) = 4 \because y ^ { \prime \prime } ( 0 ) = 4 ∵y′′(0)=4， ∴ 4 = C 1 ( 1 + 0 ) \therefore 4 = C _ { 1 }(1+0) ∴4=C1​(1+0)

∴ y ′ ′ = 4 ( 1 + x 3 ) \therefore y ^ { \prime \prime } = 4 ( 1 + x ^ { 3 } ) ∴y′′=4(1+x3)，积分得 y ′ = 4 x + x 4 + C 2 y ^ { \prime } = 4x + x ^ { 4 } + C _ { 2 } y′=4x+x4+C2​

因为 y ′ ( 0 ) = 1 y ^ { \prime } ( 0 ) = 1 y′(0)=1，所以 C 2 = 1 C _ { 2 } = 1 C2​=1

从而 y ′ = 4 x + x 4 + 1 y ^ { \prime } = 4x + x ^ { 4 } + 1 y′=4x+x4+1,再积分得 y = 2 x 2 + x 5 5 + x + C 3 y = 2x ^ { 2 } + \frac { x ^ { 5 } } { 5 } + x + C _ { 3 } y=2x2+5x5​+x+C3​.

由 y ( 0 ) = 0 y ( 0 ) = 0 y(0)=0得 C 3 = 0 C _ { 3 } = 0 C3​=0,所求解为 y = 2 x 2 + x 5 5 + x y = 2x ^ { 2 } + \frac { x ^ { 5 } } { 5 } + x y=2x2+5x5​+x

【解】因为 y 1 = e − x y _ { 1 } = e ^ { - x } y1​=e−x y 2 = 2 x e − x , y 3 = 3 e x y _ { 2 } = 2xe ^ { - x } , y _ { 3 } = 3e ^ { x } y2​=2xe−x,y3​=3ex

所以三阶常系数齐次线性微分方程的三个特征值为 λ 1 = λ 2 = − 1 , λ 3 = 1 \lambda _ { 1 } = \lambda _ { 2 } = -1 , \lambda _ { 3 } = 1 λ1​=λ2​=−1,λ3​=1,

对应的特征方程为 ( λ + 1 ) 2 ( λ − 1 ) = 0 ( \lambda + 1 ) ^ { 2 } ( \lambda - 1 ) = 0 (λ+1)2(λ−1)=0,即 λ 3 + λ 2 − λ − 1 = 0 \lambda ^ { 3 } + \lambda ^ { 2 } - \lambda - 1 = 0 λ3+λ2−λ−1=0，

故一个原方程可为 y ′ ′ + y ′ ′ − y ′ − y = 0 y ^ { \prime \prime } + y ^ { \prime \prime } - y ^ { \prime } - y = 0 y′′+y′′−y′−y=0.

x 2 − 2 x + 4 = 0 , ( x − 1 ) 2 = − 3 , x − 1 = 3 i , x = 1 ± 3 i x^2-2x+4=0, (x-1)^2 = -3,x-1=\sqrt{3}i , x = 1 \pm \sqrt{3}i x2−2x+4=0,(x−1)2=−3,x−1=3 ​i,x=1±3 ​i

https://blog.csdn.net/lynn15600693998/article/details/86597068

https://ww2.mathworks.cn/help/symbolic/dsolve.html?s_tid=srchtitle_dsolve_1

​ 用于求解常微分方程的精确解，也称为常微分方程的符号解，无初值条件则求出通解

使用方法

​ S = dsolve(eqn) ​ S = dsolve(eqn,cond) ​ S = dsolve(eqn,cond,Name,Value) ​ [y1,…,yN] = dsolve(___)

eqn表示微分方程组，cond表示初始条件或边界条件，Name表示变量

实例1 y ′ ′ + y ′ − 6 y = 0 y'' + y' -6y = 0 y′′+y′−6y=0

Maple 是一个数学软件，透过智能文件界面提供最强大的数学引擎，可以轻松分析、探索、可视化和求解数学问题