概率论的学习和整理8: 几何分布 |
您所在的位置:网站首页 › T分布的图形 › 概率论的学习和整理8: 几何分布 |
概率论的学习和整理8: 几何分布
|
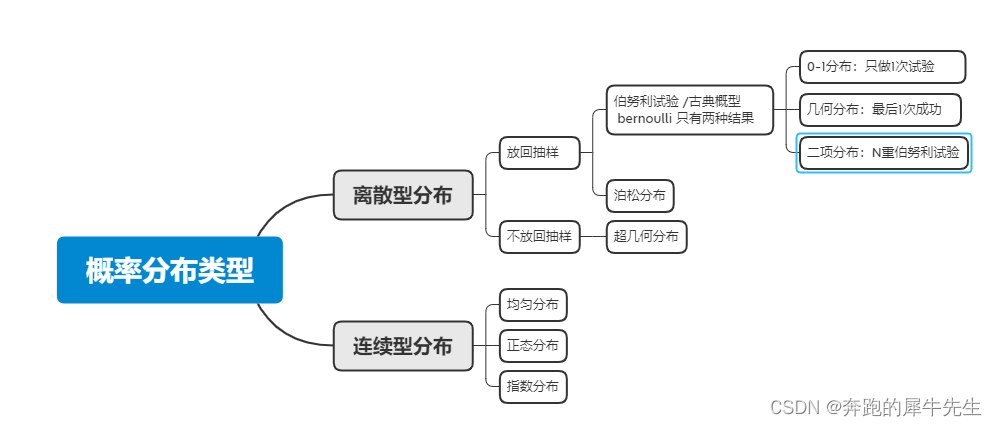
目录 前言 1 什么是几何分布 1.1 常规定义 1.2 另外一种定义 2 几何分布在概率分布中的定位 3 几何分布的 概率,期望,方差 4 为什么叫几何分布 (几何=等比) 4.1 先需要了解算术平均数和几何平均数 4.2 第1:几何布分布的,各个项之间,就是等比数据,公比为 (1-p ) 4.3 第2:几何布分布每个中间的项,都是前后两个数的几何平均数,因此得名 5 几何分布的期望 5.1 符合几何分布的变量,其期望 5.2 几何分布,其中失败次数 m的期望 6 几何分布的方差 7 几何分布的概率分布:分布率,分布函数,分布图 7.1 几何分布的分布律 7.2 几何分布的概率分布函数 7.3 几何分布的概率分布图形 8 几何分布的 期望的图形(一般很少画期望的图形) 9 具体例子:几何分布的概率,平均值,方差的多种计算对比 9.1 几何分布的一个计算例子如下 9.2 符合几何分布的随机变量n 的概率P(n=i)分布函数Pdf 9.2.1 注意Pi 和p的区别 9.2.2 随机变量n的Pi概率公式 9.2.3 Pi概率对应的pdf 和cdf的分布曲线形态 9.3 符合几何分布的随机变量n 的均值/期望值 9.4 符合几何分布的随机变量n 的方差 9.5 随机变量的该区,期望,方差和 样本/已知内容的都不同! 10 几何分布的各种图形和数据关系很大(尤其原始实验的概率p) 10.1 几何分布的一个计算例子如下 11 一个抽奖模型的例子:几何分布的应用 11.1 抽奖模型的定义 11.2 第N次抽中的概率 11.2.1 概率的函数---->pdf的朴素算法 和意义 11.3 随机变量的期望 和方差 11.3.1 期望的朴素算法和意义 11.4 随机变量的方差 11.5 如果没中,还抽多少次可以中奖 11.6抽多少可以中多少奖(n次)(中奖的期望次数----这个中奖K次就是二项分布了) 11 需要补充的, 备注检查 前言 几何分布和超几何分布,听名字很像,但实际上这两种随机变量的分布没有任何关系几何分布和二项分布关系也不大几何分布是负二项分布(帕斯卡分布)的一种特例 1 什么是几何分布 1.1 常规定义 一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的次数,这个次数所符合的概率分布即为几何分布。详细地说就是:前k-1次皆失败,第k次成功的概率。 首先几何分布,属于古典概型/ 伯努利试验,特点是:只有每次试验只可能有两种结果如果只做1次试验,那是属于0-1分布如果做n次试验,但是只有最后一次成功,则次数n这个随机变量符合 几何分布如果给定做N次试验,有k次成功,则随机变量k符合 二项分布如果做试验有k次成功,则总实验次数随机变量N符合 负二项分布 1.2 另外一种定义 几何分布实际上是一种无限分布,和二项分布,超几何分布都不一样首先,几何分布是伯努利试验,其中给p=0.1固定,且概率稳定不变要找的是第一次成功的次数n,和n的概率,方差等伯努利试验进行N次,比如可以是无限多次,假设成功标记结果为1,失败标记结果为0,那么一定存在这样的一些序列假如某一次是,如 [000000000100011000010010000100...] 而把所有标记为1的次数找出来,其中最小的那个次数 N 就是几何分布的 随机变量N而 n 可能=1,对应p=...而 n 可能=1,对应p=...而 n 可能=1,对应p=...... ...这样就可以得出 n的pdf函数,p(x=n)=(1-p)^(n-1)*p ,n=[1,∞] 2 几何分布在概率分布中的定位 下图错的,要修改图上有错,伯努利试验 和古典概型不一样古典概率,只强调所有事件概率相等,并不要求每次试验概率稳定反过来,伯努利试验只要求概率稳定,和2种结果,并不要求概率相等
几何分布的公式 在伯努利试验中,成功的概率为p若ξ表示出现首次成功时的试验次数,则ξ是离散型随机变量它只取正整数,且有P(ξ=k)=(1-p)的(k-1)次方乘以p (k=1,2,…,0=0,cdf 还是单调递增2 期望变化很大 期望的变化曲线,开始就是最高点,后面没有最高点,而且都是下降曲线!因为初始概率60%本来就很高了,造成Pi*ni 就很高,后面的都比这个低而 单次试验概率p=10%时,会有一个最高点,期望曲线先升高后降低,而 单次试验概率p=60%时,就直接开始下降了3 方差变化很大 方差的变化曲线,前期有1个低点,有1个高点方差序列和对应变化曲线,可以看到,方差最小的地方,对应的就是 期望值而 单次试验概率p=10%时,只有1个最低点--对应的是期望值的位置但是单次试验概率p=60%时,不但有1个最低点--对应的是期望值的位置,还有一个最高值。因为单次试验概率p=60%时,E(X)=1.1 这附近方差最低,而 n=4周围,方差达到了最大值,而后再降低 11 一个抽奖模型的例子:几何分布的应用 11.1 抽奖模型的定义 绝大多数的抽奖,虽然可能有多档奖励,但是用户的目标都可以抽象为,中奖,不中奖两种 (比如只关心大奖),而且中奖的概率一般都是不变的。而且用户的目标是:中奖会考虑以下问题 想知道抽第N次时,中奖的概率有多大 (概率---符合几何分布)想知道自己抽几次可以中奖(1次),(中奖的期望次数----几何分布的期望)抽多少可以中多少奖(n次)(中奖的期望次数----这个中奖K次就是二项分布了)如果没中,还抽多少次可以中奖
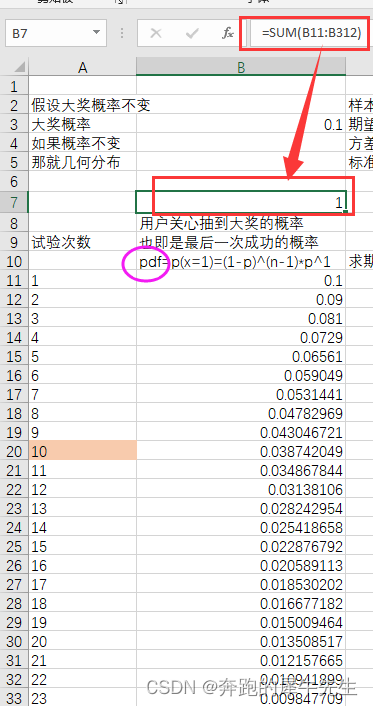
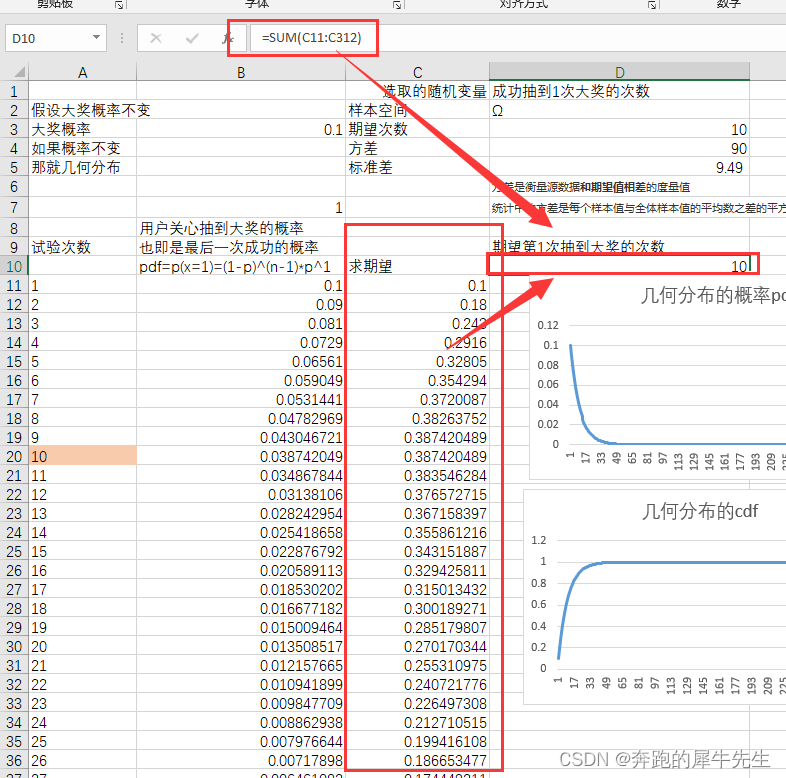
因此有些反直觉的结论 单次抽奖概率,第一次中奖概率最大,后面逐渐降低 符合几何分布的概率分布虽然累计概率cdf是一直在增大,这个符合大家的常识,也就是多抽总是越来越容易中奖但是pdf概率一直在下降第1次的抽奖概率是最大的,后面在逐渐降低从公式也可以看出来p(x=1,n)=(1-p)^(n-1)*p^1 ,当p固定的时候,p属于[0,1], n越大,p(x=n)越小p(x=1,n) 本身不是一个概率,是一个随着n 变化的 概率变化函数,有N个概率结果。pdf描述的正是这个函数的形态。 11.2.1 概率的函数---->pdf的朴素算法 和意义 pdf 就是关于 n=1~n 变化时,p(x=1) 的序列,函数这个sum 比然是等于1的。也就是cdf的最大值max=1
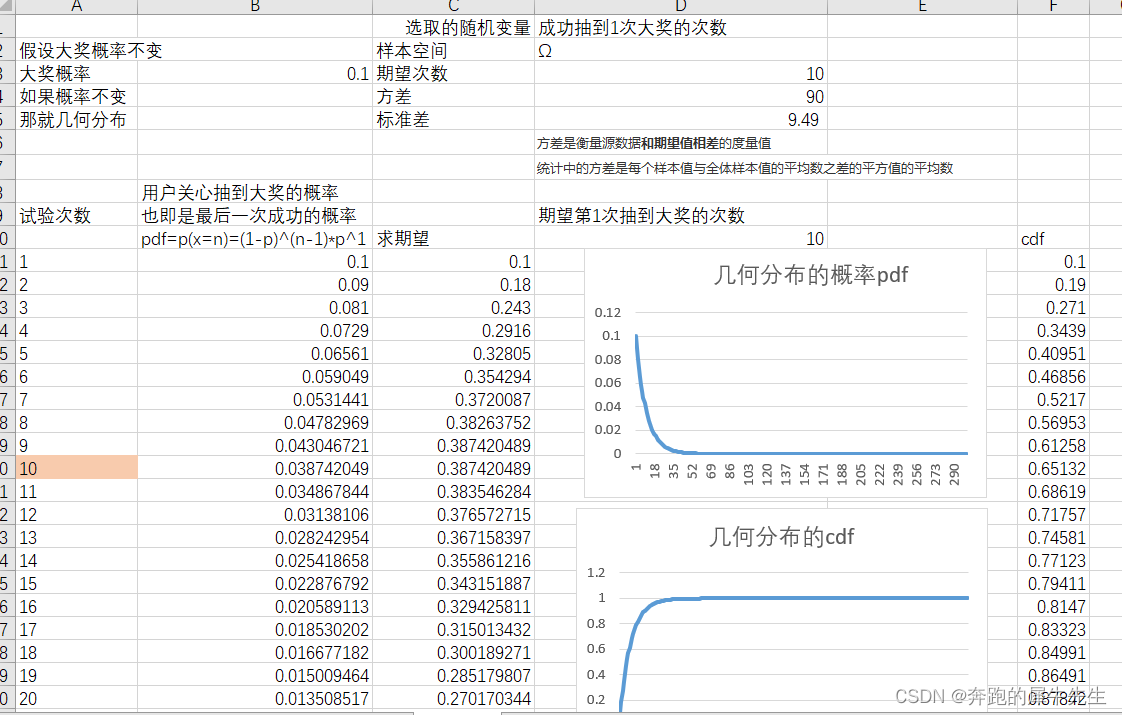
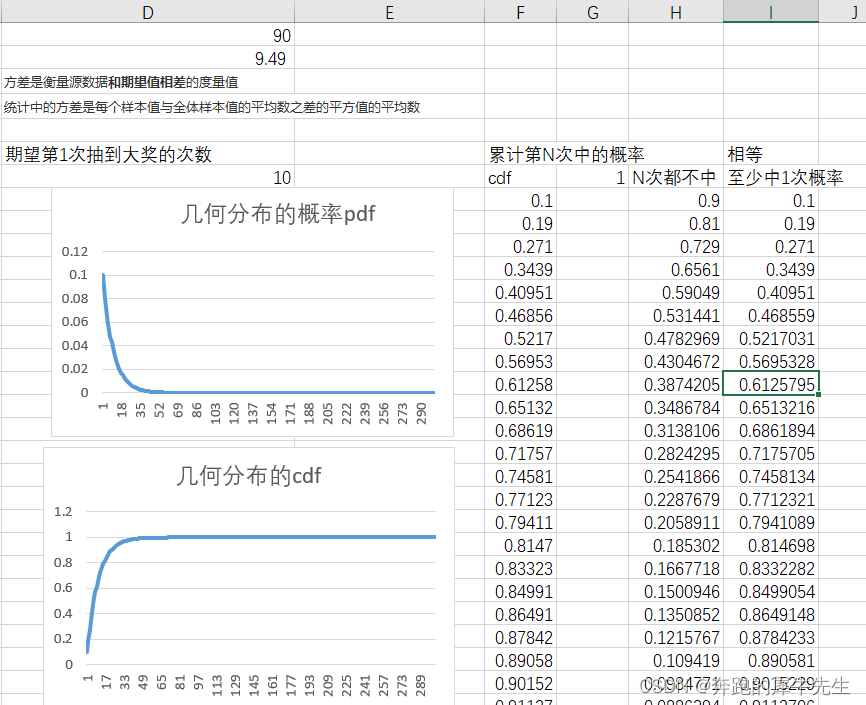
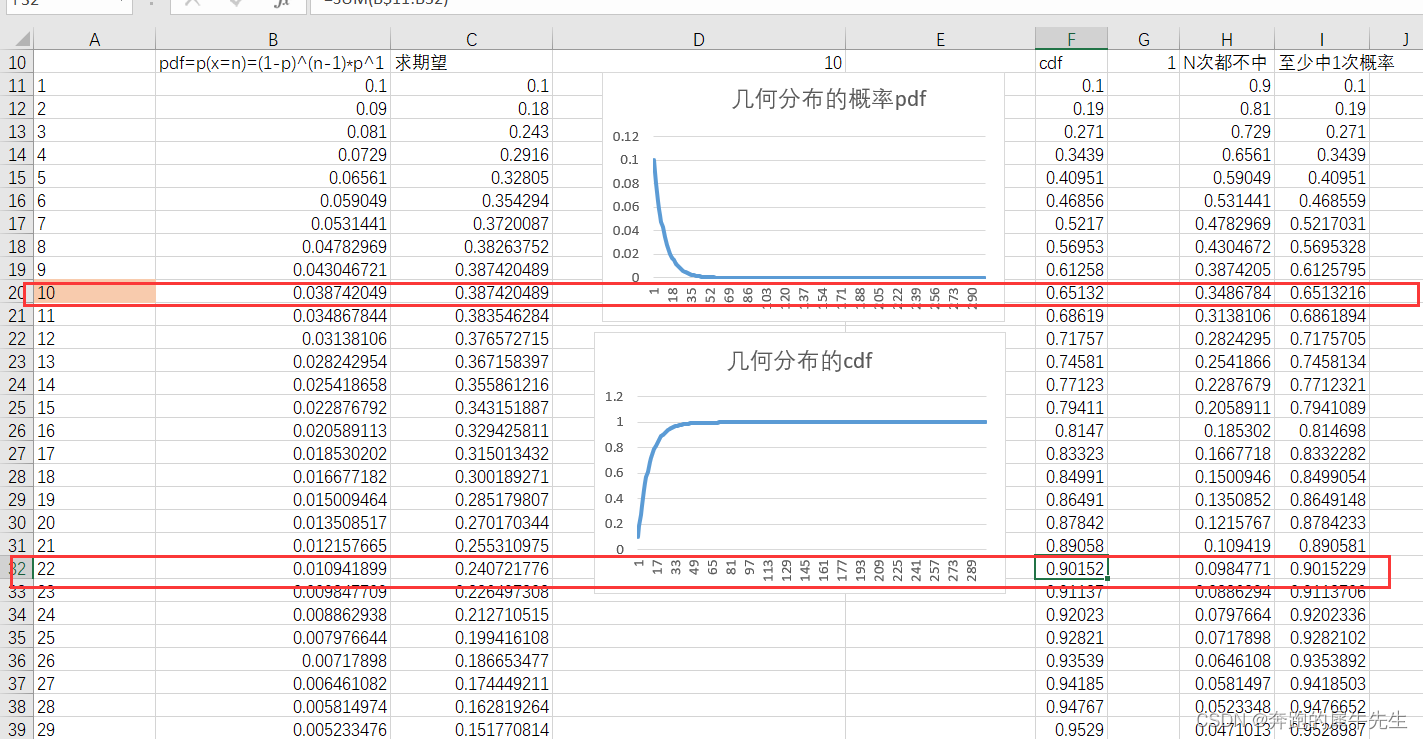
因此有些反直觉的结论 1 期望中奖次数附近对应的概率很低, 对应的累计概率并不是特别高 期望中奖次数,也就是 平均中奖次数=10但是第10次的pdf=3.8%第10次对应的cdf=65%看概率都不是很高2 几何分布的方差较大,抽奖的体验可能不太好 但是方差不小,统计中的方差是每个样本值与全体样本值的平均数之差的平方值的平均数标准差不小,标准差=9.49也就是抽奖的次数变化很大,中奖概率=cdf=1-连续不中的概率 中奖概率=Σp(x=n)=1-(1-p)^n 两种计算方法是一样的。 cdf 累计中奖的概率= 至少中1次的概率
可以看到 期望次数10次时,累计中奖概率65%而要累计90%中奖,需要大概22次,而对应22次单次抽奖中奖率才1%所以不同的人中奖概率会差别较大(后面可以改变模型,改变这个情况)
11.5 如果没中,还抽多少次可以中奖 11.6抽多少可以中多少奖(n次)(中奖的期望次数----这个中奖K次就是二项分布了) 11 需要补充的, 备注检查 1 概率的计算,有了 2 概率的意义 3 期望的意义 3 期望的公式 4 期望的朴素算复 5 方差的公式算复 6 方差的朴素算复
|
【本文地址】
今日新闻 |
推荐新闻 |