深入理解高斯消元法:解方程、线性相关和有解的条件|线性代数笔记 |
您所在的位置:网站首页 › 非线性方程组有解的条件 › 深入理解高斯消元法:解方程、线性相关和有解的条件|线性代数笔记 |
深入理解高斯消元法:解方程、线性相关和有解的条件|线性代数笔记
|
深入理解高斯消元法:解方程、线性相关和有解的条件|线性代数笔记
本文透彻讲解高斯消元法的各种意义和过程,不局限于它的解方程功能,探索更深刻的含义。先讲解解方程的过程,再介绍相关的概念、解读背后的原理。如果你已经熟悉使用高斯消元法解方程组,可选择性跳过部分内容。 本文的md源码文件:AnBlogs 文章目录 深入理解高斯消元法:解方程、线性相关和有解的条件|线性代数笔记 可逆矩阵的简单情况 看看解方程的过程 消元过程 (Elimination) 回代过程 (Backward Substitution) 联系求逆矩阵 (Inverse) 解方程的目的 不止一个解的方程 没有那么多个方程 齐次方程的解 算法 解释一下 填充单位矩阵 总结一下算法 非齐次方程 线性相关或独立 定义 秩 矩阵的各种形状和有解条件 高瘦列满秩 矮胖行满秩 综合情况 可逆矩阵的简单情况你一定会解简单的线性方程组,比如下面这样的: 这个过程可以用矩阵描述,表达的是相同含义。 把方程组左边变量前的系数放进矩阵: A = ( 2 4 − 2 4 9 − 3 − 2 − 3 7 ) A=\begin{pmatrix} 2 & 4 & -2\\ 4 & 9 & -3\\ -2 & -3 & 7\\ \end{pmatrix} A=⎝⎛24−249−3−2−37⎠⎞ 把方程组右边数字放进矩阵: b = ( 2 8 10 ) b=\begin{pmatrix} 2\\ 8\\ 10\\ \end{pmatrix} b=⎝⎛2810⎠⎞ 原方程可以写成: A x = b Ax=b Ax=b 接下来进行消元的过程。由于等式之间的加减法同时操作等式两边,以上两个矩阵 A , b A,b A,b的「行变换」需要同时进行,故把它们放进同一个矩阵: A ′ = ( 2 4 − 2 2 4 9 − 3 8 − 2 − 3 7 10 ) A'=\begin{pmatrix} 2 & 4 & -2 & 2\\ 4 & 9 & -3 & 8\\ -2 & -3 & 7 & 10\\ \end{pmatrix} A′=⎝⎛24−249−3−2−372810⎠⎞ 先消掉 ( 2 ) , ( 3 ) (2),(3) (2),(3)中的 x 1 x_1 x1,也就是把矩阵第2,3行的第一列变为0。将第1行直接加到第3行、乘2后减去第2行,可以实现这个效果: A ( 1 ) = ( 2 4 − 2 2 0 1 1 4 0 1 5 12 ) A^{(1)}=\begin{pmatrix} 2 & 4 & -2 & 2\\ 0 & 1 & 1 & 4\\ 0 & 1 & 5 & 12\\ \end{pmatrix} A(1)=⎝⎛200411−2152412⎠⎞ 相当于保持第一个方程不变,使用第一个方程,在第2,3中消去了 x 1 x_1 x1。新的第2,3方程如下: 上式可以再看成一个二元一次方程组,在其中的一个方程中消去 x 2 x_2 x2或 x 3 x_3 x3,就可以解出这个方程组,再通过带入 Equ 1 \text{Equ}_1 Equ1第一个方程解出 x 1 x_1 x1。 我们用矩阵的语言描述消去 x 2 x_2 x2的过程。在已经得到 A ( 1 ) A^{(1)} A(1)的前提下,使用第2行,把 A ( 1 ) A^{(1)} A(1)第3行第2列的数字变成0,也就是消去 x 2 x_2 x2的过程。得到的矩阵如下: A ( 2 ) = ( 2 4 − 2 2 0 1 1 4 0 0 4 8 ) A^{(2)}=\begin{pmatrix} 2 & 4 & -2 & 2\\ 0 & 1 & 1 & 4\\ 0 & 0 & 4 & 8\\ \end{pmatrix} A(2)=⎝⎛200410−214248⎠⎞ 第三行表达成方程: Equ 3 : 4 x 3 = 8 \text{Equ}_3:4x_3=8 Equ3:4x3=8 为了解出 x 3 x_3 x3,得到 x 3 = … x_3=… x3=…的形式,要给 Equ 3 \text{Equ}_3 Equ3两边同时除以 4 4 4,得到 Equ 4 : x 3 = 2 \text{Equ}_4:x_3=2 Equ4:x3=2。矩阵也对应操作, A ( 2 ) A^{(2)} A(2)第3行除以 4 4 4: A ( 3 ) = ( 2 4 − 2 2 0 1 1 4 0 0 1 2 ) A^{(3)}=\begin{pmatrix} 2 & 4 & -2 & 2\\ 0 & 1 & 1 & 4\\ 0 & 0 & 1 & 2\\ \end{pmatrix} A(3)=⎝⎛200410−211242⎠⎞ 把 x 3 x_3 x3带入 Equ 2 \text{Equ}_2 Equ2的任意一个方程都可以解出 x 2 x_2 x2。因为上步操作中,把 Equ 2 \text{Equ}_2 Equ2的第二个方程的 x 2 x_2 x2消去了,所以现在把 Equ 4 : x 3 = 2 \text{Equ}_4:x_3=2 Equ4:x3=2带入第一个方程,相当于等式两边同时减去 Equ 4 : x 3 = 2 \text{Equ}_4:x_3=2 Equ4:x3=2,得到 Equ 5 : x 2 = 2 \text{Equ}_5:x_2=2 Equ5:x2=2。对应矩阵操作,是拿 A ( 3 ) A^{(3)} A(3)的第3行去减第2行: A ( 4 ) = ( 2 4 − 2 2 0 1 0 2 0 0 1 2 ) A^{(4)}=\begin{pmatrix} 2 & 4 & -2 & 2\\ 0 & 1 & 0 & 2\\ 0 & 0 & 1 & 2\\ \end{pmatrix} A(4)=⎝⎛2 |
【本文地址】
今日新闻 |
推荐新闻 |
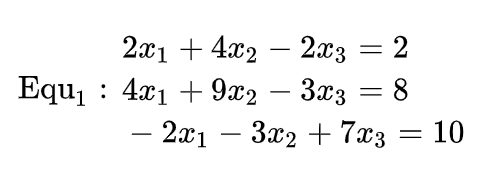 你一定知道,消元的过程就是解方程的过程。对于上面的方程组, ( 1 ) + ( 3 ) (1)+(3) (1)+(3)、 ( 1 ) × 2 − ( 2 ) (1)\times 2-(2) (1)×2−(2)可以消掉 x 1 x_1 x1,得到的两个方程进一步可以消掉 x 2 x_2 x2或 x 3 x_3 x3,进而解得结果。
你一定知道,消元的过程就是解方程的过程。对于上面的方程组, ( 1 ) + ( 3 ) (1)+(3) (1)+(3)、 ( 1 ) × 2 − ( 2 ) (1)\times 2-(2) (1)×2−(2)可以消掉 x 1 x_1 x1,得到的两个方程进一步可以消掉 x 2 x_2 x2或 x 3 x_3 x3,进而解得结果。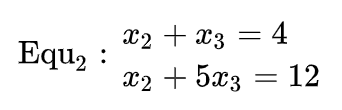 上面的操作可以看出,把矩阵的一行乘上某个数字,再加/减到另一行,可以看作把方程组中的两个方程拿出来,让他们的等式两边相互加减,就是我们熟悉的消元手法!
上面的操作可以看出,把矩阵的一行乘上某个数字,再加/减到另一行,可以看作把方程组中的两个方程拿出来,让他们的等式两边相互加减,就是我们熟悉的消元手法!