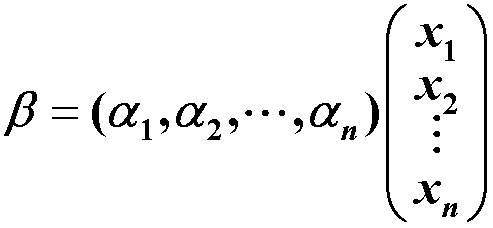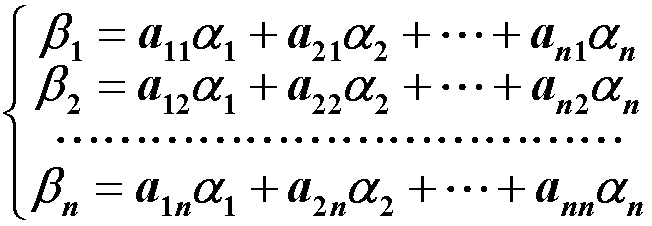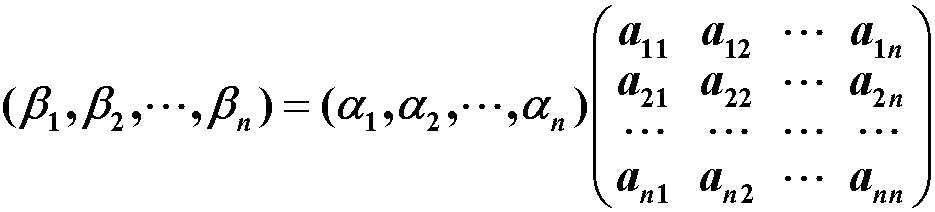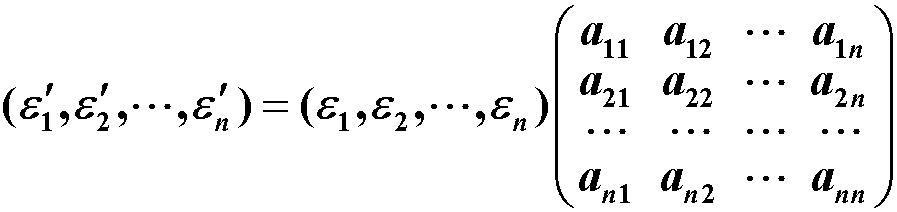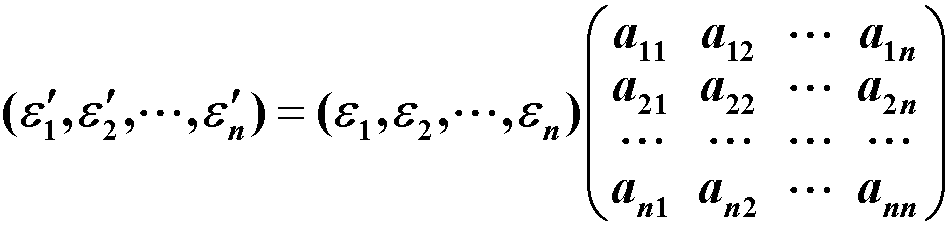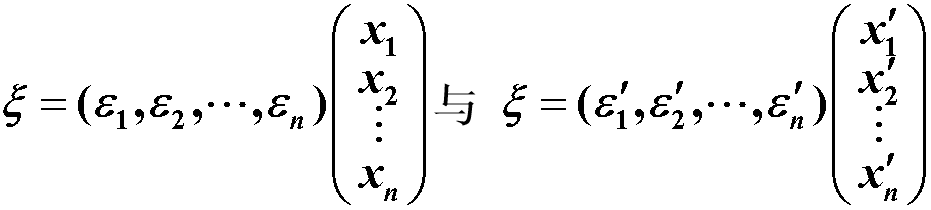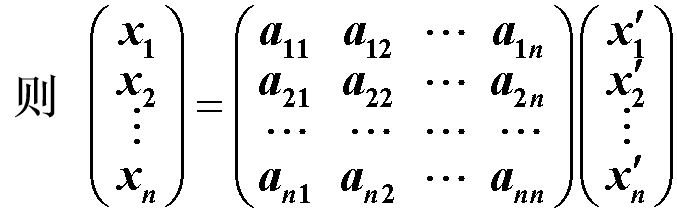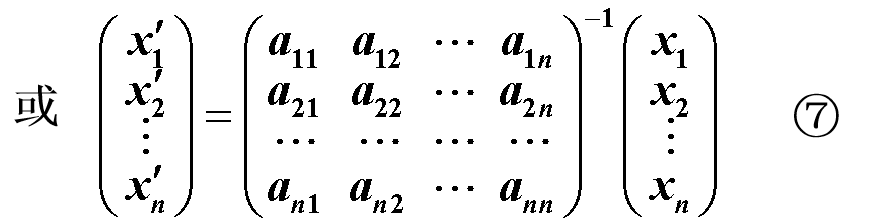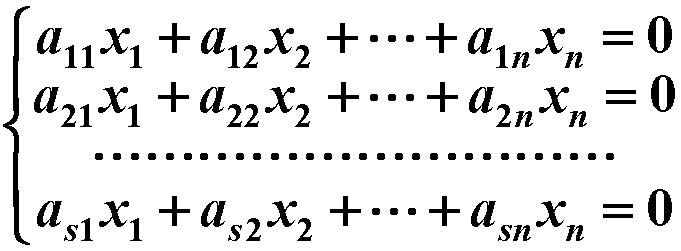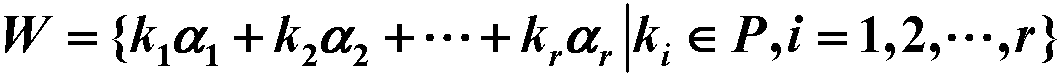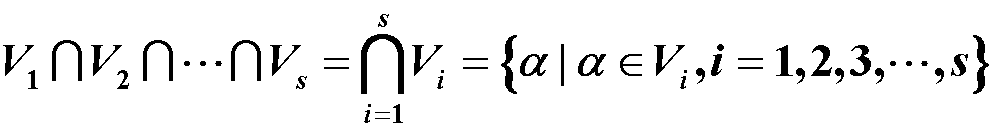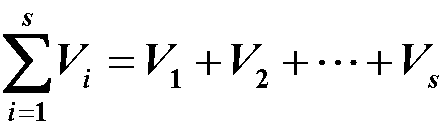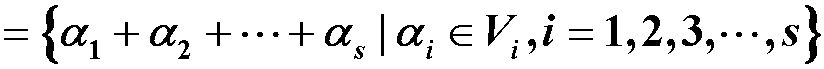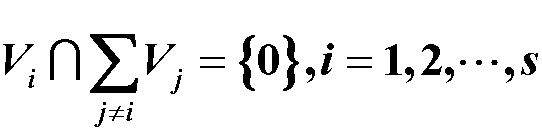数域：设P是由一些复数组成的集合，其中包括0与1，如果P中任意两个数的和、差、积、商（除数不为0）仍是P中的数，则称P为一个数域。

常见数域： 复数域C；实数域R；有理数域Q。

集合：指作为整体看的一堆东西，例如一条直线是一个由点组成的集合，一个线性方程组解的全体组成一个集合，即解集合。

元素：组成集合的东西称为这个集合的元素。

集合的描述方法：

集合间的关系：

集合间的运算：交集、并集

映射：设M、M´是给定的两个非空集合，如果有一个对应法则σ，通过这个法则σ对于M中的每一个元素a，都有M´中一个唯一确定的元素a´与它对应, 则称 σ为M到M´的一个映射，记作 σ: M → M’ 称 a´为 a 在映射σ下的象，而 a称为 a´在映射σ下的**原象，**记作 σ(a)=a’ 或 σ: a↦a’

集合M 到M 自身的映射称为M 的一个变换

设映射 σ: M → M’ ，集合 σ(M) = {σ(a)|a∈M} 称之为M在映射σ下的象，通常记作Imσ。显然，Imσ ⊆ M’

单位映射：σ把每个元素映射到它自身，称为集合M的恒等映射或单位映射，记为IM。

函数：函数可以认为是映射的一个特殊情形。

映射乘法：设映射σ: M → M’，τ: M’ → M’'，乘积τσ定义为(τσ)(a)=τ(σ(a))，即相继施行σ和τ的结果，是 M 到 M" 的一个映射。

映射的乘法结合律：设映射σ: M → M’，τ: M’ → M’‘，φ: M’’ → M’‘’，有 (φτ)σ = φ(τσ)。

映射的性质：设映射 σ: M → M’，

若 Imσ = M’，即对于任意 y ∈ M’， 均存在 x ∈ M，使 y = σ(x)，则称σ是M到M´的一个满射（或称 σ为映上的）；

若M中不同元素的象也不同，即由 a1≠a2一定有 σ(a1) ≠ σ(a2)，那么称σ是M到M´的一个单射（或称σ为1—1的）；

若σ既是单射，又是满射，则称σ为双射（或称σ为 1—1对应）

存在对于有限集来说，两集合之间存在双射的充要条件是它们所含元素的个数相同；

对于有限集A及其子集B，若B≠A（即B为A的真子集），则 A、B之间不可能存在1—1对应；但是对于无限集未必如此.

可逆映射：设映射 σ: M → M’，若有映射 τ: M’ → M，使得 τσ = IM，στ = IM，则称σ为可逆映射，τ为σ的逆映射，记作σ-1。

引进线性空间的目的：研究线性方程组解有无解，有多少解的判定，以及有无穷多解时解集的结构

线性空间的定义：设V是一个非空集合，P是一个数域，在集合V中定义了一种代数运算，叫做加法：即对∀ɑ，β ∈ V，在V中都存在唯一的一个元素γ与它们对应，称γ为ɑ与β的和，记 γ = ɑ + β；在P与V的元素之间还定义了一种运算，叫做数量乘法：即∀ɑ ∈ V，∀k ∈ P，在V中都存在唯一的一个元素δ它们对应，称δ为k与α的数量乘积，记为 δ=kα。

如果加法和数量乘法封闭且满足下述8条运算规则，则称V为数域P上的线性空间：

加法规则：

α + β = β + α

(α + β) + γ = α +（β + γ）

在V中有一个元素0，对∀ɑ ∈ V，有 α + 0 = α

（具有这个性质的元素0称为V的零元素）

对∀ɑ ∈ V，都有V中的一个元素β，使得 α + β = 0

（β 称为 α 的负元素）

数量乘法规则 :

数量乘法与加法规则：

注：

凡满足以上八条规则的加法及数量乘法也称为线性运算

线性空间的元素也称为向量，线性空间也称向量空间．但这里的向量不一定是有序数组．

若集合对于定义的加法和数乘运算不封闭，或者运算封闭但不满足八条规则中的任一条，则此集合就不能构成线性空间．

例如，对于线性空间R2，去掉其中的向量[0, 0]T，就不满足加法数乘封闭，因此就不是线性空间，所以线性空间必包含零向量；

只含一个向量—零向量{0}的线性空间称为零空间.

P[x]指数域P上的一元多项式环，表示定义在数域P上的多项式

P[x]n表示定义在数域P上的次数不超过n的多项式加上零多项式构成的空间.

Pm×n指数域P上全体m×n矩阵构成的线性空间，它是m×n维的。

线性空间的性质：

线性空间中向量之间的线性关系：在线性代数中我们知道，设V 是数域 P 上的一个线性空间，那么有：

α1,α2,···,α~r ~∈ V(r ≥1)，k1,k2,···,kr ∈ P，则式 k1α1+k2α2+···+krαr称为向量组α1,α2,···,αr的一个线性组合；

α1,α2,···,αr,β~ ~∈ V，若存在k1,k2,···,kr ∈ P，使 β = k1α1+k2α2+···+krαr，则称向量β可经向量组α1,α2,···.,αr​线性表出；

若向量组β1,β2,···,βs中每一向量皆可经向量组α1,α2,···,αr线性表出，则称向量组β1,β2,···,βs可经向量组α1,α2,···,αr​线性表出；

若两向量组可以互相线性表出，则称这两个向量组为等价的；

α1,α2,···,αr∈ V，若存在不全为零的数k1,k2,···,kr ∈ P，使 k1α1+k2α2+···+krαr = 0，则称向量组α1,α2,···,αr为线性相关的；

若仅当k1=k2=···=k1=0 时 k1α1+k2α2+···+krαr = 0 才成立，则称向量组α1,α2,···,αr为线性无关的。

结论：

向量组α1,α2,···,αr线性相关 ⇔ α1,α2,···,αr中有一个向量可经其余向量线性表出；

若向量组α1,α2,···,αr线性无关，且可被向量组β1,β2,···,βs线性表出，则 r ≤ s；

若向量组α1,α2,···,αr和向量组β1,β2,···,βs等价，则 r = s；

若向量组α1,α2,···,αr线性无关，但向量组α1,α2,···,αr,β 线性相关，则β可被向量组α1,α2,···,αr线性表出，且表示法唯一。

无限维线性空间：若线性空间 V 中可以找到任意多个线性无关的向量，则称 V 是无限维线性空间。

有限维线性空间：

线性空间的基与维数的确定：若线性空间V中的向量组α1,α2,···,αn满足:

标准基：一般地，向量空间 Pn = {(a1,a2,…,an)|ai ∈ P, i = 1,2,…,n} 为n维的，ɛ1=(1,0,…,0),ɛ2=(0,1,…,0),···,ɛn=(0,0,…,1)就是 Pn 的一组基．称为Pn 的标准基.

注：

向量的形式书写法：

则记作

基变换：设V为数域P上n维线性空间，ɛ1,ɛ2,···,ɛn，ɛ’1,ɛ’2,···,ɛ’n为V中的两组基，若

则称公式右边的系数矩阵为由基 ɛ1,ɛ2,···,ɛn 到基 ɛ’1,ɛ’2,···,ɛ’n的过渡矩阵，称上式为由基 ɛ1,ɛ2,···,ɛn到基 ɛ’1,ɛ’2,···,ɛ’n的基变换公式。

性质：

坐标变换：V为数域P上的n维线性空间，ɛ1,ɛ2,···,ɛn与 ɛ’1,ɛ’2,···,ɛ’n为V中的两组基，且

设 ξ∈V且ξ在基 ɛ1,ɛ2,···,ɛn与 ɛ’1,ɛ’2,···,ɛ’n下的坐标分别为 (x1,x2,···,xn) 与 ( x’1,x’2,···,x’n)，即

称上述两式为向量ξ在基变换下的坐标变换公式

线性子空间的定义：设V是数域P上的线性空间，集合 W ⊆ V(W≠∅)，若W对于V中的两种运算（加法和数乘）也构成数域P上的线性空间，则称W为V的一个线性子空间，简称为子空间。

注：

任一线性子空间的维数不能超过整个空间的维数

只含零向量的子集合 W = {0} 是V的一个线性子空间，称之为V的零子空间

解空间：n元齐次线性方程组

的全部解向量所成集合W对于通常的向量加法和数量乘法构成的线性空间是 n 维向量空间 Pn 的一个子空间，称W为上述方程组的解空间．

注：

生成子空间：V为数域P上的线性空间，α1,α2,···,αn为V 中的一组向量，则子空间

称为V的由α1,α2,···,α~n ~​生成的子空间，记作 L(α1,α2,···,αn)，称α1,α2,···,αn为L(α1,α2,···,αn)的一组生成元。

定理：

设W为n维线性空间V的任一子空间，α1,α2,···,αn是W的一组基，则有 W = L(α1,α2,···,αn)

α1,α2,···,αr与 β1,β2,···,βs为线性空间V中的两组向量，则 L(α1,α2,···,αr) = L(β1,β2,···,βs) ⇔ α1,α2,···,αr与 β1,β2,···,βs等价

生成子空间 L(α1,α2,···,αr) 的维数＝向量组α1,α2,···,αr的秩

推论：设α1,α2,···,αs是线性空间V中不全为零的一组向量，αi1,αi2,···,αir(r≤s)是它的一个极大无关组，则 L(α1,α2,···,αs) = L(αi1,αi2,···,αir)

设 α1,α2,···,αn为P上n维线性空间V的一组基，A为P上一个 n×s 矩阵，若 (β1,β2,···,βs) = (α1,α2,···,αn)A，则 L(β1,β2,···,βs) 的维数 = 秩(A)

扩基定理：W为 n 维线性空间 V 的一个 m 维子空间，α1,α2,···,αm为W的一组基，则这组向量必定可扩充为 V 的一组基．即在 V 中必定可找到 n－m 个向量 αm+1,αm+2,···,αn，使α1,α2,···,αm为V的一组基。

子空间的交：设V1、V2为线性空间V的子空间，则集合 V1∩V2 = {a | a ∈ V1 且 a ∈ V2}也为V的子空间，称之为V1与V2的交空间。

多个子空间的交记为

子空间的和：设V1、V2为线性空间V的子空间，则集合 V1+V2 = {a1+a2 | a1 ∈ V1 , a2 ∈ V2} 也为V的子空间，称之为V1与V2的和空间。

多个子空间的和记为

注：

子空间的交与和的有关性质：

设V1, V2, W为线性空间V的子空间：

若 W⊆V1, W⊆V2, 则 W⊆V1∩V2

若 V1⊆W, V2⊆W, 则 V1+V2⊆W

设V1, V2为线性空间V的子空间，则以下三条件等价:

V1⊆V2

V1∩V2=V1

V1+V2=V2

α1,α2,···,αr与 β1,β2,···,βs为线性空间V中的两组向量，则 L(α1,α2,···,αr) + L(β1,β2,···,βs) = L(α1,α2,···,αr, β1,β2,···,βs)

维数公式:设V1, V2为线性空间V的两个子空间，则 dimV1 + dimV2 = dim(V1+V2) + dim(V1∩V2)。可以看出，子空间的和的维数往往比子空间的维数的和要小。

推论：设V1, V2为线性空间V的两个子空间，若 dimV1 + dimV2> n，则V1、V2必含非零的公共向量. 即V1∩V2中必含有非零向量。

应用：在Pn中，用W1、W2分别表示两个齐次线性方程组的解空间，则W1∩W2就是这两个齐次线性方程组公共解的解空间。

直和的定义：设V1, V2为线性空间V的两个子空间，若和V1+V2中每个向量α的分解式 α = α1 + α2，α1∈V1, α2∈V2是唯一的，和 V1+V2就称为直和，记作V1⊕V2

直和的判定：

和V1+V2是直和 ⇔ 零向量分解式唯一，即若 α1 + α2= 0，α1∈V1, α2∈V2，则必有 α1 = α2= 0

和V1+V2是直和 ⇔ V1∩ V2={0}

和V1+V2是直和 ⇔ dimV1 + dimV2 = dim(V1+V2)

设U是线性空间V的一个子空间，则必存在一个子空间W，使 V = U ⊕ W，称这样的W为U的一个余子空间，余子空间 一般不是唯一的（除非U是平凡子空间）

设 ɛ1,ɛ2,···,ɛn，ɳ1,ɳ2,···,ɳn分别是线性子空间V1、V2中的一组基，则

和V1+V2是直和 ⇔ ɛ1,ɛ2,···,ɛn，ɳ1,ɳ2,···,ɳn线性无关

多个子空间的直和：设V1, V2,…,Vs都是线性空间V的子空间，若和V1+V2+…+Vs中每个向量α的分解式 α = α1 + α2 + … + αs，αi∈Vi, i=1,2,…,s是唯一的，则和就称为直和，记作V1⊕V2⊕…⊕Vs

多个子空间的直和的判定：和上述直和判定同理，注意：

注：每一个n 维线性空间都可以表示成n个一维子空间的直和；

同构映射的定义：设V，V’都是数域P上的线性空间，如果映射 σ：V→V’具有以下性质：

则称σ是V到V’的一个同构映射，并称线性空间V与V’同构，记作V≅V’

同构的有关结论：

数域P上任一n维线性空间都与Pn同构.

设V，V’都是数域P上的线性空间，σ是V到V’的一个同构映射，则有：

两个同构映射的乘积还是同构映射

注：同构关系具有反身性、对称性、传递性

数域P上的两个有限维线性空间 V、V’ 同构 ⇔ dimV1 = dimV2