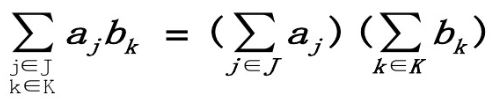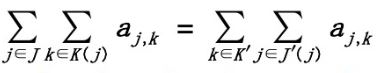求和式子的几个性质及下标变换

您所在的位置：网站首页 › 阶乘相乘化简 › 求和式子的几个性质及下标变换

求和式子的几个性质及下标变换

2024-07-15 00:36| 来源: 网络整理| 查看: 265

莫比乌斯反演化简经常用，特别是交换求和次序，下标变换

参考1

参考2

参考3（化简技巧）

例子来自《具体数学》

一.三大基本性质

二.多重和式分配律，J K独立或者J包含K

三.多重次序变换（可以类比多重积分来理解） ①j,k相互独立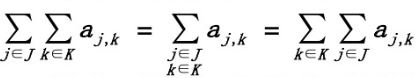

②j,k不独立

前提：

推论（例子）：

但是不能写成 $\sum_{j=1}^{k}\sum_{k=1}^{n}$

内层受外层影响，所以还可以把只含k的项提前，用分配律

例子2：（第二步k+j替换k)

四.下标变换（补充）

化简类似j|i 的整除式

①常数

$\sum_{i = 1}^{n} \sum_{j|i} j = \sum_{i = 1}^{n} i * \lfloor \frac{n}{i} \rfloor = \sum_{i = 1}^{n} \frac{\lfloor \frac{n}{i} \rfloor * ( 1 + \lfloor \frac{n}{i} \rfloor)}{2}$

②函数

$\sum_{i=1}^{n}\sum_{j|i} f(j) = \sum_{i=1}^{n}\sum_{j=1}^{\lfloor\frac{n}{i}\rfloor}f(j)$

③下标合并

$\sum_{i=1}^{n}\sum_{j|i} f(i) = \sum_{i=1}^{n}\sum_{\frac{j}{j}|\frac{i}{j}} f(\frac{i}{j}*j) = \sum_{\frac{i}{j}=1}^{n} f(\frac{i}{j}*j)=(\frac{i}{j}\rightarrow i) \sum_{i=1}^{n} f(ij)$

【本文地址】

求和式子的几个性质及下标变换

求和式子的几个性质及下标变换

今日新闻

推荐新闻