朴素贝叶斯（Naïve Bayes, NB）算法，是一种基于贝叶斯定理与特征条件独立假设的分类方法。朴素：特征条件独立；贝叶斯：基于贝叶斯定理。属于监督学习的生成模型，实现简单，并有坚实的数学理论（即贝叶斯定理）作为支撑。在大量样本下会有较好的表现，不适用于输入向量的特征条件有关联的场景。

贝叶斯定理：贝叶斯理论是以18世纪的一位神学家托马斯.贝叶斯(Thomas Bayes)命名。通常，事件A在事件B（发生）的条件下的概率，与事件B在事件A（发生）的条件下的概率是不一样的。然而，这两者是有确定的关系的，贝叶斯定理就是这种关系的陈述。

P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)​

朴素贝叶斯：朴素贝叶斯方法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入 x x x，利用贝叶斯定理求出后验概率最大的输出 y y y：

P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x j ∣ Y = c k ) P(X=x| Y=c_{k})=P(X^{(1)=}x^{(1)},...,X^{(n)=}x^{(n)}|Y=c_k)=\prod_{j=1}^{n}P(X^{(j)}=x^{j}|Y=c_k) P(X=x∣Y=ck​)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck​)=j=1∏n​P(X(j)=xj∣Y=ck​)

朴素贝叶斯算法原理：其实朴素贝叶斯方法是一种生成模型，对于给定的输入 x x x，通过学习到的模型计算后验概率分布 P ( Y = c k ∣ X = x ) P(Y=c_k | X=x) P(Y=ck​∣X=x)，将后验概率最大的类作为 x x x的类输出。其中后验概率计算根据贝叶斯定理进行：

P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) P(Y=c_{k}|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_k P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k) } P(Y=ck​∣X=x)=∑k​P(Y=ck​)∏j​P(X(j)=x(j)∣Y=ck​)P(X=x∣Y=ck​)P(Y=ck​)​

然后，最后的朴素贝叶斯分类模型为：

y = f ( x ) = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=arg max_{c_k}\frac{P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_jP(X^{(j)}=x^{(j)}|Y=c_k) } y=f(x)=argmaxck​​∑k​P(Y=ck​)∏j​P(X(j)=x(j)∣Y=ck​)P(Y=ck​)∏j​P(X(j)=x(j)∣Y=ck​)​

在高斯朴素贝叶斯中，每个特征都是连续的，并且都呈高斯分布。高斯分布又称为正态分布。 GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布：

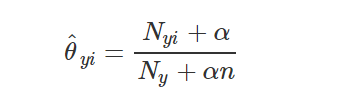MultinomialNB 实现服从多项分布数据的贝叶斯算法，是一个经典的朴素贝叶斯在文本分类中使用的变种（其中的数据是通常表示为词向量的数量，虽然TF-IDF向量在实际项目中表现得很好），对于每一个 y y y来说，分布通过向量 Θ y = ( Θ y 1 , . . . , Θ y n ) \Theta_y=(\Theta_{y1},...,\Theta_{yn}) Θy​=(Θy1​,...,Θyn​)参数化， n n n是类别的数目（在文本分类中，表示词汇量的长度）， Θ y i \Theta_{yi} Θyi​ 表示标签 i i i出现的样本属于类别 y y y的概率 P ( x i ∣ y ) P(x_i|y) P(xi​∣y)。 该参数 Θ y i \Theta_{yi} Θyi​是一个平滑的最大似然估计，即相对频率计数： N y i = ∑ x ∈ T x i N_{yi}=\sum_{x\in T}x_i Nyi​=∑x∈T​xi​：表示标签 i i i在样本集 T T T中属于类别 y y y的数目； N y = ∑ i = 1 ∣ T ∣ N y i N_{y}=\sum_{i=1}^{|T|}N_yi Ny​=∑i=1∣T∣​Ny​i：表示在所有标签中类别 y y y出现的数目。