逻辑回归算法虽然名字中含有回归二字，但却是机器学习算法中典型的监督式二分类算法模型。本文在推导逻辑回归算法过程中遵循的顺序是，首先提出假设函数、其次构造出损失函数、最后求解损失函数得出假设函数中的参数值。在构造损失函数时同样采取两种不同的方式：一是从样本数据出发，二是从统计理论着手。不同的方式最后构造出的损失函数却是一致的，文章的最后会给出逻辑回归算法梯度下降求解的矩阵迭代更新形式，以便于后续编程实现。本文的pdf版本已上传至Github，如果有需要可以自行下载。码字不易，欢迎点个赞，谢谢！

对于二分类问题逻辑回归是经常被采用的方法，逻辑回归算法就是在样本数据中寻找一个超平面，然后可以把样本数据准确的分隔成不同的类别，并且能够对相应的新数据特征进行分类。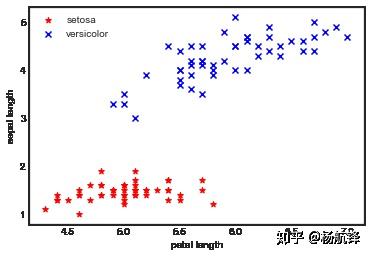

比如上图所示的两类数据样本，怎么寻找一个超平面(直线)分割开红色、蓝色样本？如果新给出一个样本的特征如何预测该样本属于哪个类别？

回顾线性回归中的假设函数 h_\theta(x)=\theta_0+\theta_1x_1+\cdots+\theta_nx_n=\theta^Tx 这表示的是一个超平面，逻辑回归中的超平面与线性回归中的超平面并无什么本质上的差异，但是线性回归是回归问题逻辑回归是分类问题两者本质上不同，线性回归中样本集中在超平面附近且没有类别差异而逻辑回归中样本点被所超平面分割且有明确的类别。因此逻辑回归的假设函数需要判断样本点在超平面上还是超平面下，所以给出一种映射关系： g(z) = \dfrac{1}{1+e^{-z}}\\ 函数 \ g(z) \ 称为 \ sigmoid \ 函数，其函数图像如下图所示：

使用 \ sigmoid\ 函数对超平面进行映射是因为它有一些很好的性质：

综上可以给出逻辑回归算法的假设函数 \ h_\theta(x)\ h_\theta(x)=g(\theta^Tx)=\dfrac{1}{1+e^{-\theta^Tx}} \\

不妨假设含有 m 个样本数据(x^{(1)},y^{(1)})、( x^{(2)},y^{(2)})、 \cdots 、(x^{(m)},y^{(m)})， y^{(i)} \in \{0,1\} 。由于 h_\theta(x) \in (0,1) ，且对于某个样本数据来说它只能属于两种类别中的某一类，所以有如下等式成立 \begin{aligned} P(y=1|x;\theta)&=h_\theta(x)\\ P(y=0|x;\theta)&=1-h_\theta(x) \end{aligned}\\

​ 构造误差函数为 \ error(h_\theta(x),y)\ \begin{aligned} error(h_\theta(x),y)&=\begin{cases} -\log h_\theta(x), & \mbox{if }y=1 \\ -\log (1-h_\theta(x)), & \mbox{if }y=0 \end{cases}\\ &=y\cdot(-\log h_\theta(x)) + (1-y)\cdot(-\log (1-h_\theta(x)))\\ &=-\left\{y\cdot(\log h_\theta(x)) + (1-y)\cdot(\log (1-h_\theta(x)))\right\} \end{aligned}\\ 至于为什么选择它作为误差函数可以从 -\log x, x \in (0,1)​ 的函数图像中得到解释:

通过对每一个样本数据计算误差函数值，损失函数 \ J(\theta) \ 即为误差函数值总和 \begin{aligned} J(\theta) &= \sum\limits_{i=1}^m error(h_\theta(x^{(i)}), y^{(i)})\\ &=\sum\limits_{i=1}^m \left\{{y^{(i)}}\cdot(-\log h_\theta(x^{(i)}))+ ({1-y^{(i)}})\cdot(-\log(1-h_\theta(x^{(i)})))\right\}\\ &=-\sum\limits_{i=1}^m \left\{{y^{(i)}}\cdot(\log h_\theta(x^{(i)}))+ ({1-y^{(i)}})\cdot(\log(1-h_\theta(x^{(i)})))\right\} \end{aligned}\\

\begin{aligned} P(y=1|x;\theta)&=h_\theta(x)\\ P(y=0|x;\theta)&=1-h_\theta(x) \end{aligned}\\

因此可以得出概率分布： \ p(y|x)=[h_\theta(x)]^{y}[1-h_\theta(x)]^{1-y}\ 。假设样本数据相互独立且同分布，所以它们的联合分布函数可以表示为各边际分布函数的乘积，故最大似然函数为 \begin{aligned} L(\theta) &=\prod\limits_{i=1}^m p(y^{(i)}|x^{(i)})\\ &=\prod\limits_{i=1}^m [h_\theta(x^{(i)})]^{y^{(i)}}[1-h_\theta(x^{(i)})]^{1-y^{(i)}} \end{aligned}\\ 对 \ L(\theta)\ 取对数从而得到对数化最大似然估计函数 \begin{aligned} \mathcal L(\theta) &= \mathcal \log(L(\theta)) \\ &= \log \prod\limits_{i=1}^m [h_\theta(x^{(i)})]^{y^{(i)}}[1-h_\theta(x^{(i)})]^{1-y^{(i)}}\\ &= \sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\} \end{aligned}\\ 求解最大化对数似然函数可得： \begin{aligned} \mathop{\arg\max}_{\theta} L(\theta) & \Leftrightarrow \mathop{\arg\max}_{\theta} \mathcal L(\theta)\\ & \Leftrightarrow \mathop{\arg\max}_{\theta} \sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\}\\ & \Leftrightarrow \mathop{\arg\min}_{\theta} -\sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\}\\ \end{aligned}\\ 即 J(\theta)=-\sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\} 。

3、小结

​ 可以发现两种方法推导出的损失函数都是一样的，下面正式定义逻辑回归模型的损失函数 $J(\theta)=-\dfrac{1}{m}\sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\} 。只是在先前的基础上乘了一个常系数 -\dfrac{1}{m} 对下一步求解 J(\theta) 的结果并不会产生影响。

最小化损失函数采用梯度下降算法，在逻辑回归中梯度下降算法的迭代格式为 \theta_j:=\theta_j-\alpha\nabla_{\theta_j} {J(\theta)}\\ 其中 \alpha\in(0,1] ​代表感知机算法的学习率，为了实现该算法首先要求出损失函数 \ J(\theta)\ 对参数 \ \theta_j\ 的梯度： \begin{aligned} \nabla_{\theta_j} J(\theta) &=- \dfrac{1}{m}\nabla_{\theta_j}\sum\limits_{i=1}^m \left\{y^{(i)} \cdot (\log h_\theta(x^{(i)})) +(1-y^{(i)})\cdot \log(1-h_\theta(x^{(i)}))\right\}\\ &=- \dfrac{1}{m}\sum\limits_{i=1}^m\left( y^{(i)} \cdot \dfrac{1}{h_\theta(x^{(i)})}\nabla_{\theta_j}h_\theta(x^{(i)}) - (1-y^{(i)})\cdot \dfrac{1}{1-h_\theta(x^{(i)})} \nabla_{\theta_j}h_\theta(x^{(i)})\right) \\ &=- \dfrac{1}{m}\sum\limits_{i=1}^m\left( y^{(i)} \cdot \dfrac{1}{h_\theta(x^{(i)})} - (1-y^{(i)})\cdot \dfrac{1}{1-h_\theta(x^{(i)})}\right)\cdot\nabla_{\theta_j}h_\theta(x^{(i)}) \\ &=- \dfrac{1}{m}\sum\limits_{i=1}^m\left( y^{(i)} \cdot \dfrac{1}{h_\theta(x^{(i)})} - (1-y^{(i)})\cdot \dfrac{1}{1-h_\theta(x^{(i)})}\right)\cdot h_\theta(x^{(i)})\cdot(1-h_\theta(x^{(i)}))\nabla_{\theta_j}\theta^Tx^{(i)}\\ &=- \dfrac{1}{m}\sum\limits_{i=1}^m \left( y^{(i)}\cdot(1-h_\theta(x^{(i)})) - (1-y^{(i)})\cdot h_\theta(x^{(i)})\right)x_j^{(i)}\\ &=- \dfrac{1}{m}\sum\limits_{i=1}^m \left( y^{(i)} - h_\theta(x^{(i)})\right)x_j^{(i)}\\ &=\dfrac{1}{m}\sum\limits_{i=1}^m \left(h_\theta(x^{(i)}) - y^{(i)}\right)x_j^{(i)} \end{aligned}\\ 因此在逻辑回归模型中利用所有的样本数据，训练梯度下降算法的完整迭代更新格式为 \theta_j:=\theta_j-\alpha \sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \ \ \ ( j\ \ for \ \ 0 \ \sim \ n)\\ 可以发现逻辑回归模型的迭代更新格式和线性回归模型的迭代更新格式完全一样，但是它们的假设函数 \ h_\theta(x)\ 的函数表达式是不一样的。

​ 向量化是使用矩阵计算来代替 for 循环 ，以简化计算过程提高效率 ，上述迭代更新的过程中有一个连加符号，如果使用 for 循环则需要执行 m 次。在此之前需要先定义一些矩阵，不妨令： \begin{aligned} Y&= \begin{bmatrix} (y^{(1)}) \\ (y^{(2)}) \\ \vdots \\ (y^{(m)}) \end{bmatrix}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta= \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}\\ ~\\ X&= \begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \vdots \\ (x^{(m)})^T \end{bmatrix} = \begin{bmatrix} 1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)} \end{bmatrix}\\ \end{aligned}\\ 则 \begin{aligned} \phi&=g(X\theta)= \begin{bmatrix} h_\theta(x^{(1)}) \\ h_\theta(x^{(2)}) \\ \vdots \\ h_\theta(x^{(m)}) \end{bmatrix} =g\left(\begin{bmatrix} \theta_0+\theta_1x_1^{(1)}+\cdots + \theta_nx_n^{(1)} \\ \theta_0+\theta_1x_1^{(2)}+\cdots + \theta_nx_n^{(2)}\\ \vdots \\ \theta_0+\theta_1x_1^{(m)}+\cdots + \theta_nx_n^{(m)} \end{bmatrix}\right)\\ ~\\ E&=h_\theta(x)-y=\phi-Y= \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_m \end{bmatrix}\\ \end{aligned}\\ 所以 \sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} = XE\\ 最后 \theta_j:=\theta_j-\alpha \sum\limits_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \ \ \ ( j\ \ for \ \ 0 \ \sim \ n)\\ 向量化后可改为 \theta:=\theta-\alpha XE\ \ \ \ \ \\

​ 逻辑回归算法是机器学习算法中比较好理解的分类模型，训练速度也很快。因为只需要存储各个维度的特征值的原因，对资源尤其是内存的占用会比较小 ，在引入了 softmax 以后可以处理多分类的问题。 任何机器学习模型都是有自己的假设，在这个假设成立的情况下模型才是适用的。逻辑回归的第一个基本假设是假设样本数据的先验分布为伯努利分布。