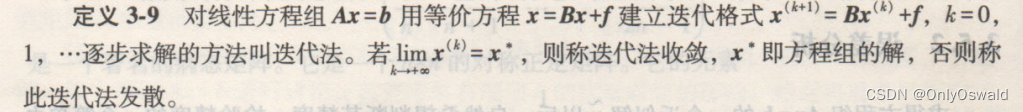迭代法求解线性方程 (简单迭代法 雅可比(Jacobi)迭代法 高斯 |
您所在的位置:网站首页 › 迭代版本命名方法是什么 › 迭代法求解线性方程 (简单迭代法 雅可比(Jacobi)迭代法 高斯 |
迭代法求解线性方程 (简单迭代法 雅可比(Jacobi)迭代法 高斯
|
本系列内容主要针对数值计算方法 第一部分 引言(误差、有效数字、减小误差的方法) 第二部分 非线性方程解法(二分法、牛顿迭代法等) 第三部分 线性方程解法(直接法和迭代法) 第四部分 差值与曲线拟合(拉格朗日、牛顿插值法、最小二乘法等) 第五部分 数值积分与数值微分(牛顿-柯特斯公式,复化积分法等) 第六部分 常微分方程的初值问题的解法 本章主要内容为迭代法求解线性方程,迭代法和直接法在求解线性方程组时各有优势和应用场景。直接法通常用于求解规模较小、系数矩阵密集的线性方程组,它通过计算系数矩阵的逆或者利用高斯消元法等方法一次性求解出所有未知数的值。而迭代法则更适合处理大型稀疏线性方程组,这是因为直接法在处理大型问题时,不仅计算量巨大,而且需要大量的存储空间来保存系数矩阵及其逆矩阵。 迭代法的基本思想是从一个初始估计解开始,通过不断迭代逼近真实解。每次迭代都根据当前的估计解来更新新的估计解,直到满足一定的精度要求或者达到预定的迭代次数。迭代法的关键在于设计一个合适的迭代公式,使得序列能够收敛到解。 一、迭代法的原理 如果说直接法像是你手中拿着地图,一眼就能看清最优路径,直接朝着目标方向快速前进。,那么迭代法好比是在迷宫中摸索前进的过程,你不断地根据当前所处位置和周围环境来调整自己的行进方向,一步步向着目标前进。 在计算机领域,迭代算法就像是使用GPS逐步调整车辆行驶方向,根据当前位置和周围环境动态更新路径,逐步朝着目的地前进。这种方法适用于那些需要多次尝试和调整才能达到最优解的问题,而直接法则更像是通过一次性的指引,直接找到最佳路径。
上式说明: x*是解向量x,从而当k充分大时 X(k)≈解问量x 式1叫简单迭代法,B叫迭代矩阵。————一阶定常迭代 注意:迭代阵 B不唯一,影响收敛性。 二、雅可比(Jacobi)迭代法理论: 雅可比迭代法又称为同时迭代法,是一种用于解线性方程组的迭代算法。其基本思想是将线性方程组的系数矩阵分解为对角线矩阵和剩余部分,并通过迭代的方式逐步逼近方程组的解。 步骤: 将系数矩阵A分解为对角线矩阵D、严格下三角矩阵L和严格上三角矩阵U。初始化初始解向量x(0)。使用迭代公式例题:先来考虑一道简单的例题 5x - y = 1 -x + 3y - z = 2 -y - z = 3不难得到对应的矩阵形式,和直接法不同,迭代法需要的矩阵是系数和解分开的两个矩阵: A = | 5 -1 0 |, b = | 1 | | -1 3 -1 | | 2 | | 0 -1 4 | | 3 | 将得到的矩阵输入到计算机中,可以编程求解,具体代码如下: #include #include #define N 3 // 假设是3x3的线性方程组 #define TOLERANCE 1e-5 // 收敛阈值 #define MAX_ITERATIONS 1000 // 最大迭代次数 void jacobiIteration(double A[N][N], double b[N], double x[N], int n) { double D_inv[N], R[N][N], x_new[N]; double max_diff; // 初始化D的逆矩阵 for (int i = 0; i < n; i++) { D_inv[i] = 1.0 / A[i][i]; } // 初始化R矩阵 for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (i == j) continue; R[i][j] = A[i][j]; } } // 迭代求解 for (int k = 0; k < MAX_ITERATIONS; k++) { for (int i = 0; i < n; i++) { x_new[i] = b[i]; for (int j = 0; j < n; j++) { x_new[i] += R[i][j] * x[j] * D_inv[j]; } } // 检查收敛性 max_diff = 0.0; for (int i = 0; i < n; i++) { max_diff = fmax(max_diff, fabs(x_new[i] - x[i])); } if (max_diff < TOLERANCE) break; // 更新解向量 for (int i = 0; i < n; i++) { x[i] = x_new[i]; } } } int main() { double A[N][N] = { {5, -1, 0}, {-1, 3, -1}, {0, -1, 4} }; double b[N] = {1, 2, 3}; double x[N] = {0, 0, 0}; // 初始解向量 jacobiIteration(A, b, x, N); printf("Solution by Jacobi Iteration:\n"); for (int i = 0; i < N; i++) { printf("x%d = %f\n", i+1, x[i]); } return 0; } 三、高斯-塞德尔(Gauss-Seidel)迭代法理论: 高斯-塞德尔迭代法(Gauss-Seidel Iteration Method)是另一种用于求解线性方程组的迭代方法。它与雅可比迭代法类似,但是每次迭代中,高斯-塞德尔法会立即使用新计算得到的值,而不是像雅可比法那样在下一次迭代中才使用。这种方法通常比雅可比迭代法收敛得更快。 步骤: 初始化:选择一个初始解向量 𝑥(0)x。迭代:对每个未知数,使用高斯-塞德尔迭代公式更新其值。收敛性检查:如果 𝑥(𝑘+1) 和 𝑥(𝑘) 之间的差异小于某个预设的阈值,则认为方程组已经求解到足够精度,停止迭代。如果未收敛,继续迭代步骤。例题: 10x - 2y - z = 1 2x + 10y + 5z = 0.5 -x - 2y + 3z = -1看到这种线性方程,依旧是先转化为矩阵的形式 : A = | 10 -2 -1 |, b = | 1 | | 2 10 5 | | 0.5 | | -1 -2 3 | | -1 | 使用高斯-塞德尔迭代法时,我们将线性方程组转换为迭代形式,并逐步逼近解。然而,此方法的成功取决于初始向量的选择和停止条件的设置。因此,在编程时,我们必须小心处理这些参数,以确保算法能够收敛并得到准确的解。 #include #include #define N 3 #define TOLERANCE 1e-5 #define MAX_ITERATIONS 1000 // 函数用于执行高斯-塞德尔迭代 void gaussSeidelIteration(double A[N][N], double b[N], double x[N]) { double x_new[N]; // 存储新的解向量 int i, j, k; double max_diff; // 存储最大的变化量 for (k = 0; k < MAX_ITERATIONS; k++) { max_diff = 0.0; // 遍历每个未知数 for (i = 0; i < N; i++) { x_new[i] = b[i]; // 计算新的解向量的每个分量 for (j = 0; j < N; j++) { if (i != j) { x_new[i] -= A[i][j] * x[j]; } } x_new[i] /= A[i][i]; // 更新最大的变化量 max_diff = fmax(max_diff, fabs(x_new[i] - x[i])); } // 判断是否达到了收敛条件 if (max_diff < TOLERANCE) break; // 更新解向量 for (i = 0; i < N; i++) { x[i] = x_new[i]; } } } int main() { double A[N][N] = { {5, -1, 0}, {-1, 3, -1}, {0, -1, 4} }; double b[N] = {1, 2, 3}; double x[N] = {0, 0, 0}; // 初始解向量 // 执行高斯-塞德尔迭代 gaussSeidelIteration(A, b, x); printf("Solution by Gauss-Seidel Iteration:\n"); for (int i = 0; i < N; i++) { printf("x%d = %f\n", i+1, x[i]); } return 0; } 四、逐次超松弛(SOR)迭代法 理论: 逐次超松弛迭代法是高斯-塞德尔迭代法的一种变体,用于加速收敛。它通过引入一个松弛因子(ω)来调整迭代过程,该因子介于1和2之间。SOR方法特别适用于大型稀疏线性系统,它利用了高斯-塞德尔法的迭代公式,但是在每次迭代中对每个未知数的更新都包含了前一次迭代的值和当前迭代的值的加权平均。 步骤: 选择松弛因子:通常介于1和2之间的某个值,记作ω。初始化解向量:选择一个初始解 𝑥(0)。迭代求解:对每个未知数,使用SOR迭代公式进行更新。检查收敛性:如果连续两次迭代的解向量之间的最大差异小于预设的阈值 𝑇𝑂𝐿𝐸𝑅𝐴𝑁𝐶𝐸,则认为方程组已经求解到足够精度,停止迭代。例题: 3x1 + 8x2 + x3 = 5 x1 - 4x2 + 10x3 = -1 -5x1 + 0.5x2 + 2x3 = 3 这里我们选定松弛因子为1.8(1.0-2.0都可以)。选定精度为小数点后六位(TOLERANCE = 1e-6) #include #include #define N 3 #define MAX_ITERATIONS 1000 #define TOLERANCE 1e-6 #define OMEGA 1.8 // 松弛因子 double A[N][N] = { {3, 8, 1}, {1, -4, 10}, {-5, 0.5, 2} }; double b[N] = {5, -1, 3}; void SOR(double x[N], double x_old[N]) { for (int i = 0; i < N; i++) { double sum = 0.0; for (int j = 0; j < N; j++) { if (i != j) { sum += A[i][j] * x_old[j]; } } x[i] = (1 - OMEGA) * x_old[i] + OMEGA * (b[i] - sum) / A[i][i]; } } int main() { double x[N], x_old[N]; // 随机初始化解向量 for (int i = 0; i < N; i++) { x[i] = x_old[i] = (double)rand() / RAND_MAX; } int iterations = 0; double max_diff; do { SOR(x, x_old); max_diff = 0.0; for (int i = 0; i < N; i++) { max_diff = fmax(max_diff, fabs(x[i] - x_old[i])); } for (int i = 0; i < N; i++) { x_old[i] = x[i]; } iterations++; } while (max_diff > TOLERANCE && iterations < MAX_ITERATIONS); printf("Solution after %d iterations:\n", iterations); for (int i = 0; i < N; i++) { printf("x%d = %f\n", i + 1, x[i]); } return 0; }本次的迭代法求解线性方程就到这里结束了,也就意味着第三章的内容已经全部更新完成,如果对我的内容有什么问题欢迎留言讨论,希望我的内容可以给大家带来帮助! |
【本文地址】
今日新闻 |
推荐新闻 |