参考 【运筹学】对偶理论 : 对称形式 ( 对称形式 | 对偶模型转化实例 | 对偶问题规律分析 ) 写出原问题线性规划的对偶问题线性规划 ,

原问题的线性规划模型 : 注意原问题的线性规划 目标函数求最大值 , 约束方程都是 小于等于不等式 ;

m a x Z = C X s . t { A X ≤ b X ≥ 0 \begin{array}{lcl} \rm maxZ = C X \\\\ \rm s.t\begin{cases} \rm AX \leq b \\\\ \rm X \geq 0 \end{cases}\end{array} maxZ=CXs.t⎩⎪⎨⎪⎧​AX≤bX≥0​​

如果原问题是求最大值 , 约束方程有大于等于不等式 , 需要在这些大于等于不等式 左右两边乘以 − 1 \rm -1 −1 , 将 大于等于不等式 转为 小于等于不等式 ;

如果进行了上述操作 , 则最终求出对偶问题后 , 系数矩阵肯定不互为转置矩阵 , 还要进行一次代换 , 令 y ′ = − y \rm y' = -y y′=−y 吗使用 − y ′ = y \rm -y' = y −y′=y 替换对偶问题中的变量 ;

对偶问题的线性规划模型 : 对偶问题 目标函数求最小值 , 约束方程都是 大于等于不等式 ;

m i n W = b T Y s . t { A T Y ≥ C T Y ≥ 0 \begin{array}{lcl} \rm minW = b^T Y \\\\ \rm s.t\begin{cases} \rm A^TY \geq C^T \\\\ \rm Y \geq 0 \end{cases}\end{array} minW=bTYs.t⎩⎪⎨⎪⎧​ATY≥CTY≥0​​

矩阵转置 : 第 1 1 1 列变第 1 1 1 行 , ⋯ \cdots ⋯ , 第 n \rm n n 列变第 n \rm n n 行 ;

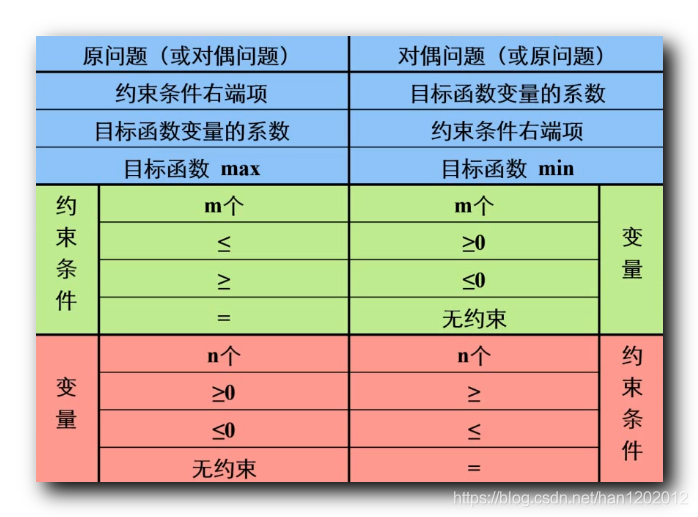
对偶示例 : 给出如下线性规划 ,

m a x Z = 2 x 1 + x 2 s . t { x 1 − 2 x 2 ≤ 8 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm maxZ = 2 x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - 2x_2 \leq 8 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} maxZ=2x1​+x2​s.t⎩⎪⎨⎪⎧​x1​−2x2​≤8x1​,x2​≥0​​

上述线性规划原问题 ① 目标函数求最大值 ② 约束方程是小于等于不等式 , ③ 约束变量大于等于 0 0 0 , 符合标准 ;

写出其对偶问题 :

( 1 ) 目标函数求最小 , 且目标函数的系数是原方程的约束方程常数 ;

m i n Z = 8 y 1 \rm minZ = 8y_1 minZ=8y1​

( 2 ) 约束条件 :

对偶问题约束方程系数 : 约束方程矩阵是 ( 1 − 2 ) \begin{pmatrix} &1 & -2 & \\ \end{pmatrix} (​1​−2​​) 的转置矩阵 ( 1 − 2 ) \begin{pmatrix} &1 & \\ &-2 & \\ \end{pmatrix} (​1−2​​) ;

对偶问题变量个数 : 约束方程的变量个数是矩阵的列数 , 这里只有 1 1 1 列 , 则只有 1 1 1 个变量 y 1 \rm y_1 y1​ ;

约束方程中间符号 : 约束条件的符号是由 原问题 变量符号决定 ( 都是 ≥ 0 \geq 0 ≥0 ) , 因此对偶问题的约束方程符号也是 ≥ \geq ≥ ;

约束方程右侧常数 : 是原问题目标函数的系数转置 , 分别是 2 , 1 2 , 1 2,1 ;

变量符号 : 对偶问题变量符号与原问题约束方程符号相反 ; 原问题约束方程是小于等于符号 , 对偶问题的变量是大于等于 0 0 0 的 ;

最终的对偶问题是 :

m i n W = 8 y 1 s . t { y 1 ≥ 2 − 2 y 1 ≥ 1 y 1 ≥ 0 \begin{array}{lcl} \rm minW = 8y_1 \\\\ \rm s.t\begin{cases} \rm y_1 \geq 2 \\\\ \rm -2y_1 \geq 1 \\\\ \rm y_1 \geq 0 \end{cases}\end{array} minW=8y1​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​y1​≥2−2y1​≥1y1​≥0​​

如果给出的原问题目标函数是求最小值 :

m i n Z = 2 x 1 + x 2 s . t { x 1 − 2 x 2 ≤ 8 x 1 , x 2 ≥ 0 \begin{array}{lcl} \rm minZ = 2 x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - 2x_2 \leq 8 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array} minZ=2x1​+x2​s.t⎩⎪⎨⎪⎧​x1​−2x2​≤8x1​,x2​≥0​​

上述线性规划的对偶问题的目标函数是求最大值 ;

参考下图列表 :

写出其对偶问题 ( 上述表格中的右侧 ) :

( 1 ) 目标函数求最大 , 且目标函数的系数是原方程的约束方程常数 ;

m i n W = 8 y 1 \rm minW = 8y_1 minW=8y1​

( 2 ) 约束条件 :

对偶问题约束方程系数 : 约束方程矩阵是 ( 1 − 2 ) \begin{pmatrix} &1 & -2 & \\ \end{pmatrix} (​1​−2​​) 的转置矩阵 ( 1 − 2 ) \begin{pmatrix} &1 & \\ &-2 & \\ \end{pmatrix} (​1−2​​) ;

对偶问题变量个数 : 约束方程的变量个数是矩阵的列数 , 这里只有 1 1 1 列 , 则只有 1 1 1 个变量 y 1 \rm y_1 y1​ ;

约束方程中间符号 : 约束条件的符号是由 原问题 变量符号决定 ( 都是 ≥ 0 \geq 0 ≥0 ) , 这里如果目标函数求最小值时原问题 , 其对偶问题约束方程符号 与 原问题变量符号相反 , 因此对偶问题的约束方程符号也是 ≤ \leq ≤ ;

约束方程右侧常数 : 是原问题目标函数的系数转置 , 分别是 2 , 1 2 , 1 2,1 ;

变量符号 : 对偶问题变量符号与原问题约束方程符号相同 ; 原问题约束方程是小于等于符号 , 对偶问题的变量是小于等于 0 0 0 的 ;

最终的对偶问题是 :

m a x Z = 8 y 1 s . t { y 1 ≤ 2 − 2 y 1 ≤ 1 y 1 ≤ 0 \begin{array}{lcl} \rm maxZ = 8y_1 \\\\ \rm s.t\begin{cases} \rm y_1 \leq 2 \\\\ \rm -2y_1 \leq 1 \\\\ \rm y_1 \leq 0 \end{cases}\end{array} maxZ=8y1​s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​y1​≤2−2y1​≤1y1​≤0​​

写出对偶定理的标准对称形式 ★ : 记住下面的标准形式

原问题 :

m a x Z = C X s . t { A X ≤ b X ≥ 0 \begin{array}{lcl} \rm maxZ = C X \\\\ \rm s.t\begin{cases} \rm AX \leq b \\\\ \rm X \geq 0 \end{cases}\end{array} maxZ=CXs.t⎩⎪⎨⎪⎧​AX≤bX≥0​​

对偶问题 :

m i n W = b T Y s . t { A T Y ≥ C T Y ≥ 0 \begin{array}{lcl} \rm minW = b^T Y \\\\ \rm s.t\begin{cases} \rm A^TY \geq C^T \\\\ \rm Y \geq 0 \end{cases}\end{array} minW=bTYs.t⎩⎪⎨⎪⎧​ATY≥CTY≥0​​

查看 约束变量的符号 与 其另外一个对偶问题的 约束方程的符号 一致性 , 来确定对偶问题的约束方程符号 ;

约束方程符号 :

如果当前线性规划问题 目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是 ≥ \geq ≥ , 因此 对偶问题的约束方程符号 与 原问题变量 符号一致 ;

如果当前线性规划问题 目标函数是求最小值 , 原问题就是下面的问题 , 其对偶问题 ( 上面的 ) 的约束方程符号是 ≤ \leq ≤ , 因此 对偶问题的约束方程符号 与 原问题变量 符号相反 ;

变量符号 :

如果当前线性规划问题 目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是 ≥ \geq ≥ , 因此 对偶问题的变量符号 与 原问题约束方程符号 符号相反 ;

如果当前线性规划问题 目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是 ≥ \geq ≥ , 因此 对偶问题的变量符号 与 原问题约束方程符号 符号一致 ;