优化 |
您所在的位置:网站首页 › 路径规划理论是什么 › 优化 |
优化
|
优化 | 考虑随机性的车辆路径规划问题详解(Stochastic VRP):模型、理论推导及Python调用Gurobi实现
0. 摘要1. 带时间窗的车辆路径规划问题(VRPTW)1.1 问题描述1.2 模型构建1.3 数值实验
2. 考虑随机性的车辆路径规划问题简介 (SVPR)2.1 问题分类2.2 建模方式
3. 考虑需求不确定性的VRPTW:数学模型、模型转化和代码实现3.1 数学模型3.2 理论推导:模型转化3.3 Python调用Gurobi求解
4. VRPTW 和SVRPTW的结果分析和对比5. 小结与思考完整代码获取方式参考文献
作者:樵溪子,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,硕士在读 审校:刘兴禄,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,博士在读 0. 摘要本文首先介绍了带时间窗的车辆路径规划问题(VRPTW)的问题描述、模型建立,并用python调用Gurobi进行求解。之后简要概述了考虑随机性的VRP问题(SVRPTW)的问题类型和建模方式。主要针对考虑需求随机性的VRPTW问题(VRPTWSD),以机遇约束规划 (Chance-constrainted programming) 的方式建模,通过理论推导将不确定性约束转化为确定性约束,然后用python调用Gurobi进行求解。 本文的模型参考自文献: [1] Desaulniers, Guy, Jacques Desrosiers, and Marius M. Solomon, eds. Column generation. Vol. 5. Springer Science & Business Media, 2006. [2] Stewart Jr, William R., and Bruce L. Golden. “Stochastic vehicle routing: A comprehensive approach.” European Journal of Operational Research 14.4 (1983): 371-385. 1. 带时间窗的车辆路径规划问题(VRPTW) 1.1 问题描述VRPTW问题定义在一队车辆 V \mathcal{V} V、一组客户 C \mathcal{C} C和一个有向图 G \mathcal{G} G上。图 G \mathcal{G} G由 ∣ C ∣ + 2 |\mathcal{C}|+2 ∣C∣+2个点组成,其中客户由 1 , 2 , . . . , n 1,2,...,n 1,2,...,n表示,车站由 0 0 0(始发站)和 n + 1 n+1 n+1(终点站)表示。所有节点的集合可表示为 N = { 0 , 1 , . . . , n + 1 } \mathcal{N}=\{0,1,...,n+1\} N={0,1,...,n+1}。所有边的集合 A \mathcal{A} A表示了车站与客户之间,以及客户之间的有向连接。其中没有边从 0 0 0点终止或者从 n + 1 n+1 n+1点开始。每一条弧 ( i , j ) , i ≠ j (i,j),i \neq j (i,j),i=j都对应一个成本 c i j c_{ij} cij和时间 t i j t_{ij} tij,时间可以包括在弧 ( i , j ) (i,j) (i,j)上的行驶时间和在 i i i点的服务时间。所有车辆通常是同质化的,每辆车都存在容量上限 Q Q Q,每一个客户 i i i点都有需要被满足的需求 d i d_i di,并且需要在时间窗 [ a i , b i ] [a_i,b_i] [ai,bi]之内被服务[1]。待优化的问题即为,如何决策车辆访问客户的路径,使得在满足一定约束的条件下,实现最小化总成本的目标。 1.2 模型构建(1) 参数 V \mathcal{V} V:车辆集合, V = { 0 , 1 , . . . , V } \mathcal{V}=\{0,1,...,V\} V={0,1,...,V}; C \mathcal{C} C:客户点的集合, C = { 1 , 2 , . . . , n } \mathcal{C}=\{1,2,...,n\} C={1,2,...,n}; N \mathcal{N} N:所有节点的集合, N = { 0 , 1 , . . . , n + 1 } \mathcal{N}=\{0,1,...,n+1\} N={0,1,...,n+1}; c i j c_{ij} cij:从 i i i到 j j j的行驶距离; d i d_i di: i i i点的客户需求量; Q Q Q:车辆容量; t i j t_{ij} tij:从 i i i点到 j j j点的行驶时间,以及服务 i i i点的时间之和; [ a i , b i ] [a_{i},b_{i}] [ai,bi]:访问 i i i点的时间窗; M i j M_{ij} Mij:足够大的正数。(2) 决策变量 s i k s_{ik} sik:车辆 k k k服务 i i i点的开始时刻; x i j k x_{ijk} xijk:车辆路径决策变量 x i j k = { 1 , 车辆 k 从弧 ( i , j ) 上经过 0 , 其他 x_{ijk}= \begin{cases} 1, & 车辆k从弧(i,j)上经过\\ 0, & 其他 \end{cases} xijk={1,0,车辆k从弧(i,j)上经过其他(3)混合整数规划模型 基于上述决策变量和参数,VRPTW可以被建模为下面的混合整数规划模型。 min ∑ k ∈ V ∑ i ∈ N ∑ j ∈ N c i j x i j k s . t . ∑ i ∈ C d i ∑ j ∈ N x i j k ⩽ Q ∀ k ∈ V , ∑ k ∈ V ∑ j ∈ N x i j k = 1 ∀ i ∈ C , ∑ j ∈ N x 0 j k = 1 ∀ k ∈ V , ∑ i ∈ N x i h k − ∑ j ∈ N x h j k = 0 ∀ h ∈ C , ∀ k ∈ V , ∑ i ∈ N x i , n + 1 , k = 1 ∀ k ∈ V , s i k + t i j − M i j ( 1 − x i j k ) ⩽ s j k , ∀ i , j ∈ N , ∀ k ∈ V , a i ⩽ s i k ⩽ b i ∀ i ∈ N , ∀ k ∈ V , x i j k ∈ { 0 , 1 } ∀ i , j ∈ N , ∀ k ∈ V s i k ≥ 0 ∀ i ∈ N , ∀ k ∈ V \begin{align} \min \quad &\sum_{k \in \mathcal{V}} \sum_{i \in \mathcal{N}}\sum_{j \in \mathcal{N}} c_{ij}x_{ijk} && \\ s.t. \quad &\sum_{i \in \mathcal{C}}d_i \sum_{j \in \mathcal{N}} x_{ijk} \leqslant Q \quad && \forall k \in \mathcal{V}, \\ & \sum_{k \in \mathcal{V}} \sum_{j \in \mathcal{N}} x_{ijk} =1 \quad &&\forall i \in \mathcal{C}, \\ &\sum_{j \in \mathcal{N}}x_{0jk}=1 \quad && \forall k \in \mathcal{V},\\ & \sum_{i \in \mathcal{N}} x_{ihk}-\sum_{j \in \mathcal{N}}x_{hjk}=0 \quad && \forall h \in \mathcal{C}, \forall k \in \mathcal{V},\\ & \sum_{i \in \mathcal{N}}x_{i,n+1,k}=1 \quad \forall k \in \mathcal{V},\\ %&x_{ijk}(s_{ik}+t_{ij}-s_{jk}) \leqslant 0 \quad &&\forall i,j \in \mathcal{N}, \forall k \in \mathcal{V},\\ & s_{ik}+t_{ij}-M_{ij}(1-x_{ijk}) \leqslant s_{jk}, \quad&& \forall i,j \in \mathcal{N}, \forall k \in \mathcal{V}, \\ &a_i \leqslant s_{ik} \leqslant b_i \quad && \forall i \in \mathcal{N}, \forall k \in \mathcal{V},\\ & x_{ijk} \in \{0,1\} \quad && \forall i,j \in \mathcal{N}, \forall k \in \mathcal{V}\\ & s_{ik} \geq 0\quad && \forall i \in \mathcal{N}, \forall k \in \mathcal{V} \end{align} mins.t.k∈V∑i∈N∑j∈N∑cijxijki∈C∑dij∈N∑xijk⩽Qk∈V∑j∈N∑xijk=1j∈N∑x0jk=1i∈N∑xihk−j∈N∑xhjk=0i∈N∑xi,n+1,k=1∀k∈V,sik+tij−Mij(1−xijk)⩽sjk,ai⩽sik⩽bixijk∈{0,1}sik≥0∀k∈V,∀i∈C,∀k∈V,∀h∈C,∀k∈V,∀i,j∈N,∀k∈V,∀i∈N,∀k∈V,∀i,j∈N,∀k∈V∀i∈N,∀k∈V 下面是各个约束的具体含义: 目标函数(1)最小化总体行驶距离;约束(2)说明车辆的载重量不能超过其容量上限;约束(3)保证了每个客户点都被访问了一次;约束(4-6)分别保证了每辆车必须从始发站出发,到达并离开每个客户点,并最终回到终点站;约束(7)规定了车辆 k k k开始服务 j j j点的时刻 s j k s_{jk} sjk,不能早于开始服务 i i i点的时刻 s i k s_{ik} sik,加上从 i i i点到 j j j点的行驶时间以及服务 i i i点的时间之和 t i j t_{ij} tij,其中 M i j M_{ij} Mij的取值下界为 b i + t i j − a j b_i+t_{ij}-a_j bi+tij−aj;约束(8)使得开始服务 i i i点的时刻是在规定的时间窗范围内;约束(9-10)是对于决策变量的约束。 1.3 数值实验本文使用的算例为Solomn算例中的c101.txt ,利用前25个客户点作为数据集并调用Gurobi求解。 求解日志 Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm]) Thread count: 8 physical cores, 8 logical processors, using up to 8 threads Optimize a model with 5513 rows, 5103 columns and 33684 nonzeros Model fingerprint: 0x0167fefc Variable types: 189 continuous, 4914 integer (4914 binary) Coefficient statistics: Matrix range [1e+00, 1e+04] Objective range [1e+00, 4e+01] Bounds range [1e+00, 1e+03] RHS range [1e+00, 1e+04] Presolve removed 4256 rows and 1953 columns Presolve time: 0.04s Presolved: 1257 rows, 3150 columns, 20472 nonzeros Variable types: 189 continuous, 2961 integer (2961 binary) Root relaxation: objective 1.840273e+02, 468 iterations, 0.01 seconds (0.01 work units) Nodes | Current Node | Objective Bounds | Work Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time 0 0 184.02728 0 60 - 184.02728 - - 0s 0 0 184.02728 0 36 - 184.02728 - - 0s 0 0 184.02728 0 36 - 184.02728 - - 0s 0 0 184.02728 0 31 - 184.02728 - - 0s 0 0 184.02728 0 31 - 184.02728 - - 0s H 0 0 193.0414573 184.02728 4.67% - 0s 0 0 184.02728 0 28 193.04146 184.02728 4.67% - 0s 0 0 184.02728 0 28 193.04146 184.02728 4.67% - 0s 0 0 184.04305 0 31 193.04146 184.04305 4.66% - 0s 0 0 184.04305 0 15 193.04146 184.04305 4.66% - 0s H 0 0 192.6417404 184.04305 4.46% - 0s 0 0 184.04305 0 20 192.64174 184.04305 4.46% - 0s 0 0 184.04305 0 15 192.64174 184.04305 4.46% - 0s H 0 0 191.8136198 184.04305 4.05% - 0s 0 0 cutoff 0 191.81362 191.81362 0.00% - 0s Cutting planes: Learned: 1 Gomory: 5 Implied bound: 3 Clique: 14 MIR: 4 RLT: 1 Relax-and-lift: 1 Explored 1 nodes (1814 simplex iterations) in 0.26 seconds (0.35 work units) Thread count was 8 (of 8 available processors) Solution count 3: 191.814 192.642 193.041 Optimal solution found (tolerance 1.00e-04) Best objective 1.918136197787e+02, best bound 1.918136197787e+02, gap 0.0000% 结果输出 Model status : 2 Objective value: 191.81 Vehicle capacity: 200.00 Vehicle id | Route 1 | [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 26] 4 |[0, 13, 17, 18, 19, 15, 16, 14, 12, 26] 6 | [0, 20, 24, 25, 23, 22, 21, 26] Vehicle id | Route length Travel distance Loads 1 | 13 59.49 160.00 4 | 10 95.88 190.00 6 | 8 36.44 110.00 结果可视化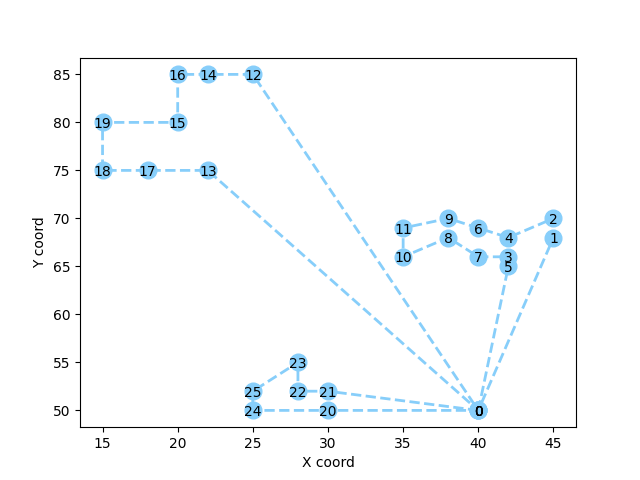 2. 考虑随机性的车辆路径规划问题简介 (SVPR)
2.1 问题分类
2. 考虑随机性的车辆路径规划问题简介 (SVPR)
2.1 问题分类
考虑随机性的车辆路径规划问题,从随机性的内容出发可以分为多种类型[3],例如: (1)随机需求(VRPSD):客户的需求量是随机变量;(2)随机客户(VRPSC):客户以一定概率出现,但是有确定的需求量;(3)随机客户和需求(VRPSCD):客户以一定概率出现,且需求量也随机;(4)随机行驶时间(VRPTWSTT):在两点之间的行驶时间,以及服务时间是随机变量。 2.2 建模方式SVPR问题的建模方法主要有以下几种: (1)机会约束规划,Chance constrained program (CCP)(2)带补偿的随机规划,Stochastic program with recourse (SPR)(3)动态规划,Dynamic programming (DP)(4)鲁棒优化,Robust optimization (RO)本文主要针对考虑需求随机性的VRPTW问题,以机遇约束规划 (Chance-constrainted programming) 的方式建模,通过理论推导将不确定性约束转化为确定性约束,然后调用Gurobi求解。 3. 考虑需求不确定性的VRPTW:数学模型、模型转化和代码实现上文提到了多种参数的不确定性,例如需求不确定、客户不确定等,但是不同的不确定因素的处理方法有一定的相似之处。本小节就以需求量不确定为例来介绍考虑随机因素的VRP的建模和模型重构方法。此外,为了帮助读者能加深理解,本文提供了完整的实现代码。 3.1 数学模型Chance-constrainted programming最早由Charnes 和Cooper提出[4,5],该模型将VRPTW中的车辆容量确定性约束(2) 转化为机会约束(13)。 min ∑ k ∈ V ∑ i ∈ N ∑ j ∈ N c i j x i j k s . t . ( 3 ) − ( 10 ) , P [ ∑ i , j d i x i j k ⩽ Q ] ⩾ 1 − α , ∀ k ∈ V . \begin{align} \min \quad &\sum_{k \in \mathcal{V}} \sum_{i \in \mathcal{N}}\sum_{j \in \mathcal{N}} c_{ij}x_{ijk} && \\ s.t. \quad & (3)-(10),\\ &P\bigg[\sum_{i,j} d_i x_{ijk} \leqslant Q \bigg ] \geqslant 1-\alpha, \quad && \forall k \in \mathcal{V}. \\ \end{align} mins.t.k∈V∑i∈N∑j∈N∑cijxijk(3)−(10),P[i,j∑dixijk⩽Q]⩾1−α,∀k∈V. 其中 P [ ∑ i ∈ C d i ∑ j ∈ N x i j k ⩽ Q ] P\bigg[\sum_{i \in \mathcal{C}}d_i \sum_{j \in \mathcal{N}} x_{ijk} \leqslant Q \bigg ] P[∑i∈Cdi∑j∈Nxijk⩽Q]代表了车辆载重未超过容量上限的概率, α \alpha α代表了该约束被违背的最大接受概率。 d i d_i di此处是一组独立分布的随机变量,代表了每个客户点的随机需求量。 注意,不同的 d i d_i di也许会服从不同的分布,但是,一些模型重构的方法对 d i d_i di的分布一般会有一定的要求,所以这里需要具体问题具体分析。 3.2 理论推导:模型转化在推导模型之前,我们先给出模型推导的大体思路。一般情况下,处理机会约束的方法,就是通过模型转化,将带有概率表达式的约束转化为确定性的不等式,从而使模型可以直接求解。下面,就来具体介绍本文考虑的随机约束的转化方法。 在上述模型中,约束(13)可以被转化为确定性约束。对于所有客户 ∀ i ∈ C \forall i \in \mathcal{C} ∀i∈C而言,若其需求 d i d_i di是一组独立分布的随机变量,其需求的均值为 μ i \mu_i μi,标准差为 σ i \sigma_i σi。基于此,对于车辆 k k k而言,其行驶路径上访问的客户的总需求的均值和标准差可以用下面的表达式来计算: 总需求的均值 M k = ∑ i , j μ i x i j k \begin{align} M_k = \sum_{i,j}\mu_ix_{ijk} \end{align} Mk=i,j∑μixijk 总需求的标准差 S k = ∑ i , j σ i 2 x i j k 2 \begin{align} S_k = \sqrt{\sum_{i,j}\sigma_i^2x_{ijk}^2} \end{align} Sk=i,j∑σi2xijk2 若存在常数 τ \tau τ使得 P [ ( ∑ i , j d i x i j k − M k ) / S k ⩽ τ ] = 1 − α , \begin{align} P\bigg[\bigg(\sum_{i,j} d_i x_{ijk} - M_k \bigg)/ S_k \leqslant \tau \bigg ] = 1-\alpha, \end{align} P[(i,j∑dixijk−Mk)/Sk⩽τ]=1−α, 则约束(16)可以被表示为如下确定性约束 M k + τ S k ⩽ Q , ∀ k ∈ V . \begin{align} M_k + \tau S_k \leqslant Q, \quad \forall k \in \mathcal{V}. \end{align} Mk+τSk⩽Q,∀k∈V. 若写为展开形式,可知约束(17)是非线性约束: ∑ i , j μ i x i j k + τ ∑ i , j σ i 2 x i j k 2 ⩽ Q , ∀ k ∈ V . \begin{align} \sum_{i,j}\mu_ix_{ijk} + \tau \sqrt{\sum_{i,j}\sigma_i^2x_{ijk}^2} \leqslant Q, \quad \forall k \in \mathcal{V}. \end{align} i,j∑μixijk+τi,j∑σi2xijk2 ⩽Q,∀k∈V. 当需求的分布满足一定条件时,非线性约束(16)可以转化为关于 μ i \mu_i μi的线性约束[2]。 定理 \quad 如果需求 d i d_i di满足: (1)需求 d i d_i di的概率分布是独立的;(2) ( ∑ i , j d i x i j k − M k ) / S k (\sum_{i,j} d_i x_{ijk} - M_k )/ S_k (∑i,jdixijk−Mk)/Sk和 ( d i − μ i ) / σ i (d_i-\mu_i)/\sigma_i (di−μi)/σi拥有相同的分布,且对所有 i i i成立;(3) σ i 2 \sigma_i^2 σi2是 μ i \mu_i μi的常数倍,即 σ i 2 = π μ i \sigma_i^2 = \pi \mu_i σi2=πμi, 则存在常数 Q ‾ \overline{Q} Q使得线性约束 ∑ i , j μ i x i j k ⩽ Q ‾ , ∀ k ∈ V . \begin{align} \sum_{i,j}\mu_ix_{ijk}\leqslant \overline{Q}, \quad \forall k \in \mathcal{V}. \end{align} i,j∑μixijk⩽Q,∀k∈V. 和机会约束(13)和(14),以及确定性约束(15)和(16)是等价的。证明 \quad VRP和SVRP问题中的决策变量 x i j k x_{ijk} xijk是0-1决策变量,则有 ( x i j k ) 2 = x i j k (x_{ijk})^2 = x_{ijk} (xijk)2=xijk。因此, S k = ∑ i , j σ i 2 x i j k 2 = ∑ i , j π μ i x i j k = π ∑ i , j μ i x i j k = π M k . \begin{align} S_k = \sqrt{\sum_{i,j} \sigma_i^2 x_{ijk}^2} = \sqrt{\sum_{i,j} \pi\mu_i x_{ijk}} =\sqrt{\pi\sum_{i,j} \mu_i x_{ijk}} = \sqrt{\pi M_k}. \end{align} Sk=i,j∑σi2xijk2 =i,j∑πμixijk =πi,j∑μixijk =πMk . 将(20)带入(17)则有 M k + τ π M k ⩽ Q . \begin{align} M_k + \tau \sqrt{\pi M_k} \leqslant Q. \end{align} Mk+τπMk ⩽Q. 进而得到 M k ⩽ 2 Q + τ 2 π − τ 4 π 2 + 4 Q τ 2 π 2 = Q ‾ . \begin{align} M_k \leqslant \frac{2Q+\tau^2\pi - \sqrt{\tau^4\pi^2 + 4Q\tau^2\pi}}{2} = \overline{Q}. \end{align} Mk⩽22Q+τ2π−τ4π2+4Qτ2π =Q. 即 ∑ i , j μ i x i j k ⩽ Q ‾ . \begin{align} \sum_{i,j}\mu_ix_{ijk}\leqslant \overline{Q}. \end{align} i,j∑μixijk⩽Q. 多种分布均满足上述定理的要求,例如泊松分布、正态分布、二项分布、伽马分布等。 因此,若需求的分布满足上述定理的要求,则转化后的模型是如下容量约束为 Q ‾ \overline{Q} Q的VRPTW问题: min ∑ k ∈ V ∑ i ∈ N ∑ j ∈ N c i j x i j k s . t . ( 3 ) − ( 10 ) , ∑ i , j μ i x i j k ⩽ Q ‾ , ∀ k ∈ V . \begin{align} \min \quad &\sum_{k \in \mathcal{V}} \sum_{i \in \mathcal{N}}\sum_{j \in \mathcal{N}} c_{ij}x_{ijk} && \\ s.t. \quad & (3)-(10),\\ &\sum_{i,j}\mu_ix_{ijk}\leqslant \overline{Q}, \quad && \forall k \in \mathcal{V}. \\ \end{align} mins.t.k∈V∑i∈N∑j∈N∑cijxijk(3)−(10),i,j∑μixijk⩽Q,∀k∈V. 3.3 Python调用Gurobi求解为了方便读者加深理解,本小节使用Python调用Gurobi求解上文介绍的数学规划模型,并给出求解结果的可视化。 我们使用Solomn VRPTW benchmark instance算例中的c101.txt,利用前25个客户点作为数据集。假设客户需求是一组独立的随机变量 d 0 , d 1 , . . . , d n d_0,d_1,...,d_n d0,d1,...,dn,其中每个 d i d_i di都服从正态分布,均值 μ i \mu_i μi等于原始数据中的需求量 d ‾ i \overline{d}_i di,方差 σ i 2 = π μ i \sigma_i^2 = \pi\mu_i σi2=πμi ( π = 0.5 \pi = 0.5 π=0.5)。 主体代码(完整代码获取方式见文末) class ModelBuilder(object): def __init__(self, data): self.data = data self.x = {} self.s = {} self.v = 5 # velocity of each vehicle self.M = 10000 # a sufficiently large number self.alpha = 0.1 # the maximum allowable probability of route failure self.mu = [] # mean self.sigma = [] # standard deviation def stochastic_demand(self, pi): """ demand at each customer: normal distribution """ # mean demand = demand from data® self.mu = copy.deepcopy(self.data.demand) # std = sqrt(pi * mu) for i in range(len(self.mu)): self.sigma.append(math.sqrt(pi * self.mu[i])) # update demand value = random variable value for i in range(len(self.data.demand)): self.data.demand[i] = np.random.normal(self.mu[i],self.sigma[i],1)[0] # chance constraint: capacity r = norm.ppf(1-self.alpha, 0, 1) Q = self.data.vehicle_capacity self.Q = (2 * Q + r**2 * pi - math.sqrt(r**4 * pi**2 + 4 * Q * r**2 * pi))/2 def build_model(self, data=None, stochastic=False, pi=0, result_path=''): self.model = None self.model = Model('SVRPTW') """ create the decision variables """ for i in self.data.node_id: for k in range(self.data.vehicle_number): self.s[i,k] = self.model.addVar(lb=0, ub=self.data.due_time[-1], vtype=GRB.CONTINUOUS, name='s_'+str(i)+'_'+str(k)) for j in self.data.node_id: if ( i!= j ): self.x[i,j,k] = self.model.addVar(lb=0, ub=1, vtype=GRB.BINARY, name='x_'+str(i)+'_'+str(j)+'_'+str(k)) self.model.update() """ (1) set the objective function """ obj = LinExpr() for i in self.data.node_id: for j in self.data.node_id: for k in range(self.data.vehicle_number): if ( i!= j ): c = self.data.distance_matrix[i][j] obj.addTerms(c, self.x[i,j,k]) self.model.setObjective(obj, GRB.MINIMIZE) """ (2) add constraints : vehicle capacity limit (stochastic or not) """ if not stochastic: self.Q = self.data.vehicle_capacity for k in range(self.data.vehicle_number): lhs = LinExpr() for i in self.data.customer_id: d = self.data.demand[i] for j in self.data.node_id: if ( i!= j ): lhs.addTerms(d,self.x[i,j,k]) self.model.addConstr(lhs |
【本文地址】