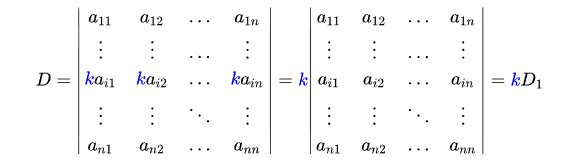
如果A是一个矩阵（n*n方阵），则det(A)或| A |表示和A对应的n阶行列式，是一个标量。 行列式值直接求解（1阶行列式的值等于其唯一元素值）：

2阶矩阵的行列式： ∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix} a_{11} ; a_{12} \\ a_{21} ; a_{22} \end{vmatrix} =a_{11} a_{22} - a_{12}a_{21} ∣∣∣∣​a11​a21​​a12​a22​​∣∣∣∣​=a11​a22​−a12​a21​

3阶矩阵的行列式： ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 11 a 23 a 32 − a 12 a 21 a 33 \begin{vmatrix} a_{11} ; a_{12} ; a_{13} \\ a_{21} ; a_{22} ; a_{23} \\ a_{31} ; a_{32} ; a_{33} \end{vmatrix} =a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{11} a_{23} a_{32} - a_{12}a_{21}a_{33} ∣∣∣∣∣∣​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​∣∣∣∣∣∣​=a11​a22​a33​+a12​a23​a31​+a13​a21​a32​−a13​a22​a31​−a11​a23​a32​−a12​a21​a33​

n阶行列式中，位于第 i i i行 j j j列的元素 a i j a_{ij} aij​，划去其所在的行和列，剩下的n-1阶行列式称为 a i j a_{ij} aij​的余子式，余子式的值乘以 ( − 1 ) i + j (-1)^{i+j} (−1)i+j就是 a i j a_{ij} aij​的代数余子式的值。

代数余子式可以简化行列式值的求解，因为有如下定理：行列式的值等于，它其中任意行（或列）所有元素与其代数余子式乘积的和。

以下3阶行列式:

∣ 3 5 1 1 2 3 4 2 1 ∣ \begin{vmatrix} 3 ; 5 ; 1 \\ 1 ; 2 ; 3 \\ 4 ; 2 ; 1 \end{vmatrix} ∣∣∣∣∣∣​314​522​131​∣∣∣∣∣∣​

其值为： 3 ∗ 2 ∗ 1 + 5 ∗ 3 ∗ 4 + 1 ∗ 1 ∗ 2 − 3 ∗ 3 ∗ 2 − 5 ∗ 1 ∗ 1 − 1 ∗ 2 ∗ 4 = 37 3*2*1+5*3*4+1*1*2-3*3*2-5*1*1-1*2*4 = 37 3∗2∗1+5∗3∗4+1∗1∗2−3∗3∗2−5∗1∗1−1∗2∗4=37

若取最后一行元素（4、2、1）分解为代数余子式求解： 4的余子式为：

∣ 5 1 2 3 ∣ \begin{vmatrix} 5 ; 1 \\ 2 ; 3 \end{vmatrix} ∣∣∣∣​52​13​∣∣∣∣​

4在第3行第1列（或第2行第0列，虽不影响结果，但行列式的行列都是从1开始数），所以代数余子式值为 ( − 1 ) 3 + 1 ∗ ( 5 ∗ 3 − 1 ∗ 2 ) = 13 (-1)^{3+1}*(5*3-1*2) = 13 (−1)3+1∗(5∗3−1∗2)=13 同理2和1的代数余子式值分别为-8、1。所以行列式的值为 4 ∗ 13 + 2 ∗ ( − 8 ) + 1 ∗ 1 = 37 4*13+2*(-8)+1*1 = 37 4∗13+2∗(−8)+1∗1=37

行列式还有如下性质：

在行列式中，某一行（列）有公因子k，则可以提出k

在行列式中，某一行（列）的每个元素是两数之和，则此行列式可拆分为两个相加的行列式

交换某两行（或两列）行列式值的符号改变。

行列式某一行（或列）元素全是0，则值为0。

行列式某一行（或列）乘以一个常数加到另一行（或列）上，行列式值不变。

利用最后一个性质可以简化行列式值求解（行列式值的简单求法）：

我们可以经过变换将行列式最后一行转化为只有最后一个元素不为0（只要用最后一列分别乘以某个数加到其他列上，总能把最后一行非末元素变为0的）。 然后利用行列式代数余子式展开求值法，可得此行列式值等于最后元素乘以其余子式的值。而其余子式也可以用以上方法进行变换，转化为最后行只有末元素不为零…… 事实上，我们能够经过一系列转换，将行列式对角线下面的所有元素都转化为零，然后求值，这时候行列式的值等于位于其对角线上的所有元素的乘积。

下面的java程序递归实现了将行列式转为三角行列式（对角线下元素全为0）的步骤——