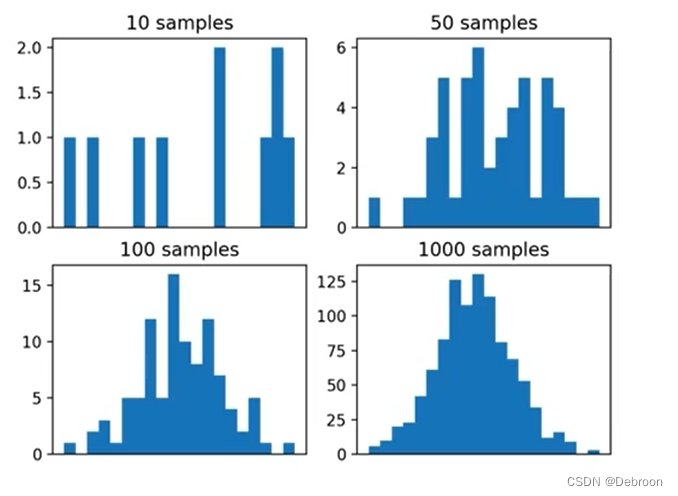
蒙特卡洛方法：一种近似复杂概率分布的随机采样方法。

假设你有一家包子店，但你不确定每天应该准备多少个包子。

你知道如果包子不够卖，会失去收入；如果包子剩太多，又会浪费食材。

问题是，你不知道每天会来多少顾客，每个顾客会买多少个包子。

这时候，你可以用一种叫做蒙特卡洛方法的技巧来帮助你做决策。

这个方法的基本思想是这样的：

观察：首先，你观察过去几天或几周的情况，记录下来工作日和周末每天的顾客数量，以及他们买的包子数量。

模拟：接着，你通过这些信息来模拟可能的情况。比如，你可以用抽签的方式来决定明天每个顾客可能的行为。每个签上写着“买1个包子”或“买2个包子”这样的信息。

重复：你把这个过程重复100次。就像你有100个不同的明天，每个明天都可能有不同的顾客数和购买情况。

计算：每次模拟结束后，你计算一下如果是这种情况，你的店会有多少利润。比如，如果张三来了买1个包子，李四买了2个，总共卖出的包子数量和利润是多少。

平均：最后，你把这100次模拟的利润加起来，然后除以100，得到一个平均值。这个平均值可以告诉你，基于以往的情况，你可以期望的大概利润是多少。

蒙特卡洛方法就像是你在做一个实验，通过反复随机模拟明天的情况，来帮助你决定应该准备多少个包子。

换成数学语言就是 – 蒙特卡洛方法就是对问题中的随机事件进行取样，为有限个样本进行独立计算，最后把样本结果进行统计的策略。

什么时候可以采用蒙特卡洛法？

蒙特卡洛的性质：

蒙特卡洛的采样，是从概率分布中随机抽取样本，从而得到分布的近似。

s = ∫ p ( x ) f ( x ) d x = E p [ f ( x ) ] s ^ n = 1 n ∑ i = 1 n f ( x ( i ) ) . \begin{aligned}s&=\int p(\boldsymbol{x})f(\boldsymbol{x})d\boldsymbol{x}=E_p[f(\mathbf{x})]\\\\\hat{s}_n&=\frac1n\sum_{i=1}^nf(\boldsymbol{x}^{(i)}).\end{aligned} ss^n​​=∫p(x)f(x)dx=Ep​[f(x)]=n1​i=1∑n​f(x(i)).​

s 是一个数学期望（平均值），我们可以想象一个随机过程，比如抽签，每次抽签都对应一个结果 x，并且每个结果 x 都有一个概率 p(x)。

函数 f(x) 是我们对每次抽出的结果 x 做的某种操作，比如可以是计算 x 的平方、加倍等等。

公式中的 ∫ p(x)f(x)dx 是一个积分，意思是对所有可能的结果 x，将每个结果的概率 p(x) 与操作后的值 f(x) 相乘，然后把这些乘积加在一起。这就给了我们一个加权平均，也就是 s。

这个期望值 s 是说：如果我们无限次地重复抽签过程，每次都对结果做操作 f(x)，那么平均下来，每次操作的结果会是多少。

这个公式的问题在于，实践中，某个概率分布 p ( x ) f ( x ) p(x)f(x) p(x)f(x) 难以采样。

数学上提供了 重要性抽样（Importance sampling），解决这个问题。

以下就是重要性抽样的数学公式：

p ( x ) f ( x ) = q ( x ) p ( x ) f ( x ) q ( x ) . s ^ q = 1 n ∑ i = 1 , x ( i ) ∼ q n p ( x ( i ) ) f ( x ( i ) ) q ( x ( i ) ) \begin{aligned}p(\boldsymbol{x})f(\boldsymbol{x})&=q(\boldsymbol{x})\frac{p(\boldsymbol{x})f(\boldsymbol{x})}{q(\boldsymbol{x})}.\\\hat{s}_q&=\frac1n\sum_{i=1,\boldsymbol{x}^{(i)}\thicksim q}^n\frac{p(\boldsymbol{x}^{(i)})f(\boldsymbol{x}^{(i)})}{q(\boldsymbol{x}^{(i)})}\end{aligned} p(x)f(x)s^q​​=q(x)q(x)p(x)f(x)​.=n1​i=1,x(i)∼q∑n​q(x(i))p(x(i))f(x(i))​​

当问题涉及到高维空间，使用重要性抽样 + 蒙特卡洛方法，还是难以计算。

我们可以使用马尔科夫链的蒙特卡洛方法来解决这个问题。

比如在巨大城堡，里面有很多房间，找到每个房间里的人数分布情况（每个房间被访问的次数），但是你不能一次进入所有的房间并计数。

你从房间A开始，记录房间A里的人数。

然后，根据一个规则（假设转移概率是基于房间的人数，人数较多的房间具有较高的转移概率），你随机选择一个相邻的房间作为下一个状态。

你进入该房间，记录房间的人数，并再次根据规则选择下一个房间。

你不断重复这个过程，记录不同房间的人数。

因为你是根据随机规则进行选择的，所以你会以一种随机的方式在不同的房间之间移动。

但是，当你重复这个过程很多次时，你会发现你更有可能停留在人数更多的房间，而在人数较少的房间停留的次数较少。

你最终会得到一个状态序列，其中房间的停留次数与该房间的人数成正比。

当你重复这个过程很多次时，你会更多地停留在人数较多的房间，从而获得与人数分布相关的结果。

虽然你不能直接计算每个房间的人数，但通过马尔科夫链的蒙特卡洛方法，你可以从任意状态（房间）开始采样，并最终收敛到目标分布（人数分布）。