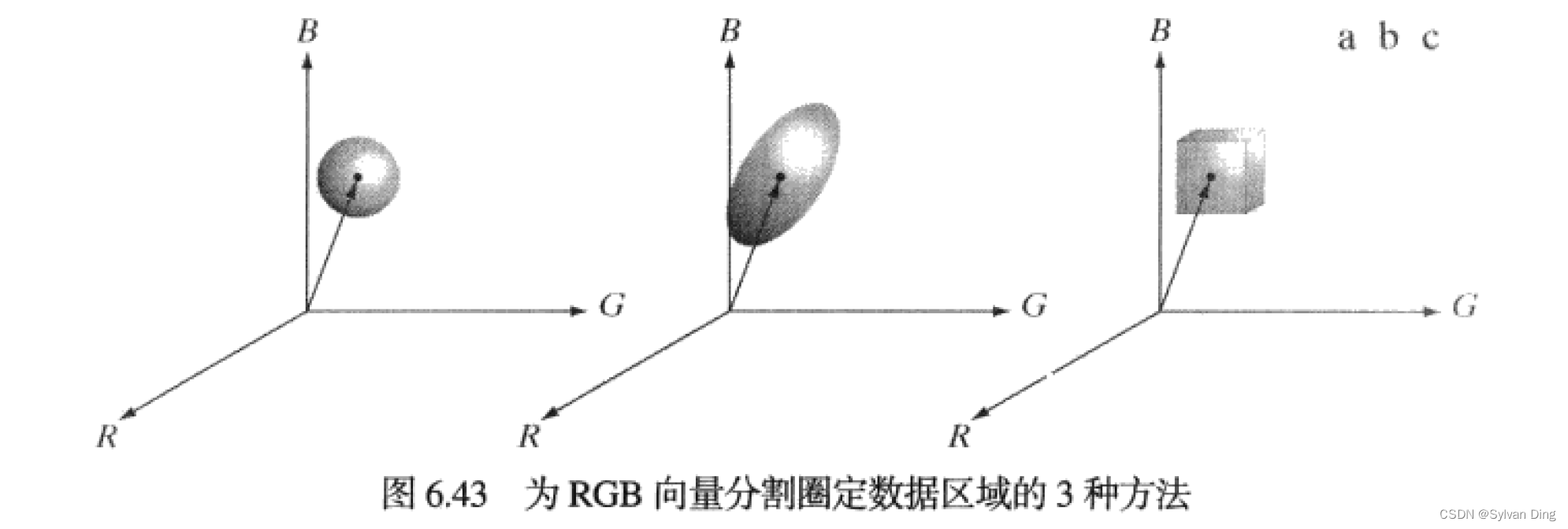
⭐️ 为尊重原创性！转载请注明出处：©️ Sylvan Ding’s Blog

本文论述了基于欧式距离和曼哈顿距离的彩色图像分割算法，并用python实现了各个算法。之后将二者的优势结合，提出了改进后的曼哈顿距离算法：基于加权曼哈顿距离的彩色图像分割算法，在分割效果和速度上超越了传统的欧式距离分割算法。

在一幅RGB图像中分割某个指定的颜色区域（bbox）的物体。给定一个感兴趣的有代表性色彩的彩色样点集，可得到我们希望分割的颜色的“平均”估计。平均彩色用RGB向量 α \alpha α表示，分割的目的是将图像中每个RGB像素分类，即在指定的区域内是否有一种颜色。为了执行这一比较，需要有相似性度量：欧氏距离和曼哈顿距离。

D ( z , α ) = ∥ z − α ∥ = [ ( z − α ) T ( z − α ) ] 1 2 = [ ( z R − a R ) 2 + ( z G − a G ) 2 + ( z B − a B ) 2 ] 1 2 D(z, \alpha)=\|z-\alpha\|=\left[(z-\alpha)^{\mathrm{T}}(z-\alpha)\right]^{\frac{1}{2}}=\left[\left(z_{R}-a_{R}\right)^{2}+\left(z_{G}-a_{G}\right)^{2}+\left(z_{B}-a_{B}\right)^{2}\right]^{\frac{1}{2}} D(z,α)=∥z−α∥=[(z−α)T(z−α)]21​=[(zR​−aR​)2+(zG​−aG​)2+(zB​−aB​)2]21​

其中，下标R、G、B表示向量 α \alpha α和 z z z的RGB分量。满足 D ( z , α ) ≤ D 0 D(z,\alpha)\le D_0 D(z,α)≤D0​的点的轨道是半径为 D 0 D_0 D0​的实心球体，包含在球体内部和表面上的点满足指定的色彩准则。对图像中两组点进行二值化，就产生了一幅二值分割图像。

有时会对欧氏距离进行推广，一种推广形式就是 D ( z , α ) = [ ( z − α ) T C − 1 ( z − α ) ] 1 / 2 D(z,\alpha)=[(z-\alpha)^TC^{-1}(z-\alpha)]^{1/2} D(z,α)=[(z−α)TC−1(z−α)]1/2，其中 C C C是表示我们希望分割的有代表性颜色的样本的协方差矩阵，描述了一个椭球体，其主轴面向最大数据扩展方向。当 C = I 3 × 3 C=I_{3\times 3} C=I3×3​时，上式退化为“球形”欧氏距离。

由于欧式距离是正的且单调的，所以可用距离的平方运算来代替，从而避免开方运算，所以我们最终的欧氏距离表达式为：

D E ( z , α ) = ( z − α ) T ( z − α ) D_E(z,\alpha)=(z-\alpha)^T(z-\alpha) DE​(z,α)=(z−α)T(z−α)

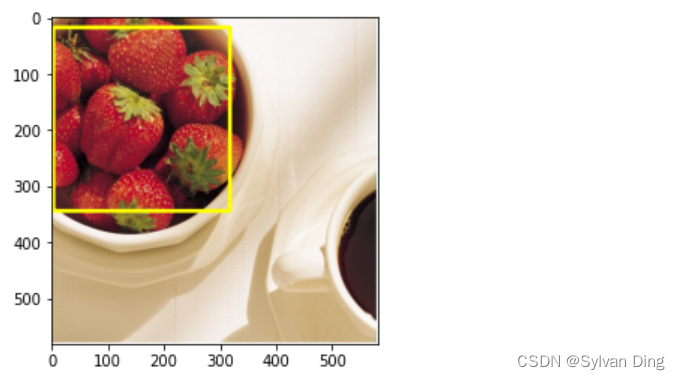
但是，上式计算代价较高，故使用曼哈顿距离（RGB空间中的盒边界）可以大幅降低计算代价。其核心思想是在盒中心 α \alpha α处，沿每一个颜色轴选择的维数与沿每个轴的样本的标准差成比例，标准差的计算只使用一次样本颜色数据。

在单通道上（以R通道为例），曼哈顿距离的定义为：

D M R ( z R , α R ) = ∣ z R − α R ∣ D_{MR}(z_R,\alpha_R)=|z_R-\alpha _R| DMR​(zR​,αR​)=∣zR​−αR​∣

需要满足的色彩准则为：

D M R ≤ η σ R D_{MR} \le \eta \sigma _R DMR​≤ησR​

其中， σ R \sigma _R σR​是样本点红色分量的标准差， η \eta η是标准差的系数，通常取 1.25 1.25 1.25。

根据上述定义，多通道平均曼哈顿距离如下：

D M ( z , α ) = ∣ ∣ z − α ∣ ∣ L 1 = ∣ z R − α R ∣ + ∣ z G − α G ∣ + ∣ z B − α B ∣ D_{M}(z,\alpha)=||z-\alpha ||_{L1}=|z_R-\alpha _R|+|z_G-\alpha _G|+|z_B-\alpha _B| DM​(z,α)=∣∣z−α∣∣L1​=∣zR​−αR​∣+∣zG​−αG​∣+∣zB​−αB​∣

D M ≤ η   ∣ ∣ σ ∣ ∣ L 1 D_{M} \le \eta \ ||\sigma ||_{L1} DM​≤η ∣∣σ∣∣L1​

其中， σ = ( σ R , σ G , σ B ) \sigma=(\sigma _R,\sigma _G,\sigma _B) σ=(σR​,σG​,σB​)是三通道各自的标准差向量。

为R、G、B每个通道设定各自的 η \eta η，则需要满足的色彩标准为：

D M R ≤ η R σ R D_{MR} \le \eta_R \sigma _R DMR​≤ηR​σR​

D M G ≤ η G σ G D_{MG} \le \eta_G \sigma _G DMG​≤ηG​σG​

D M B ≤ η B σ B D_{MB} \le \eta_B \sigma _B DMB​≤ηB​σB​