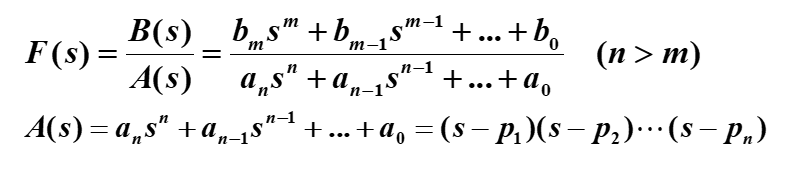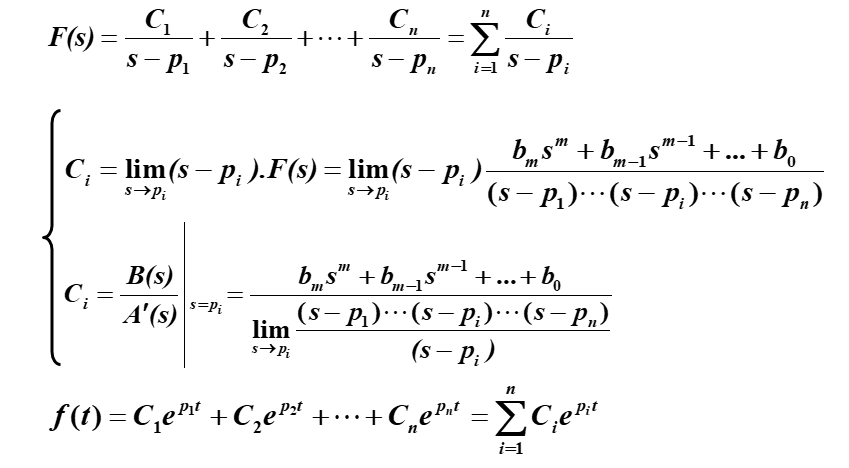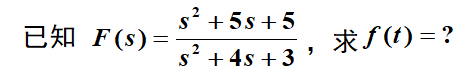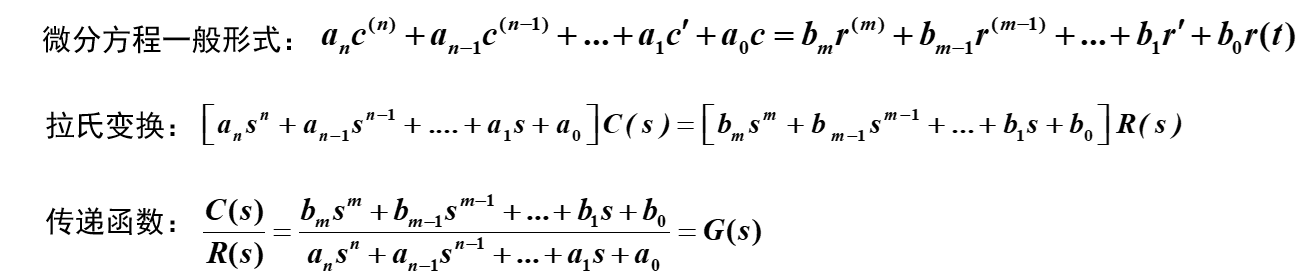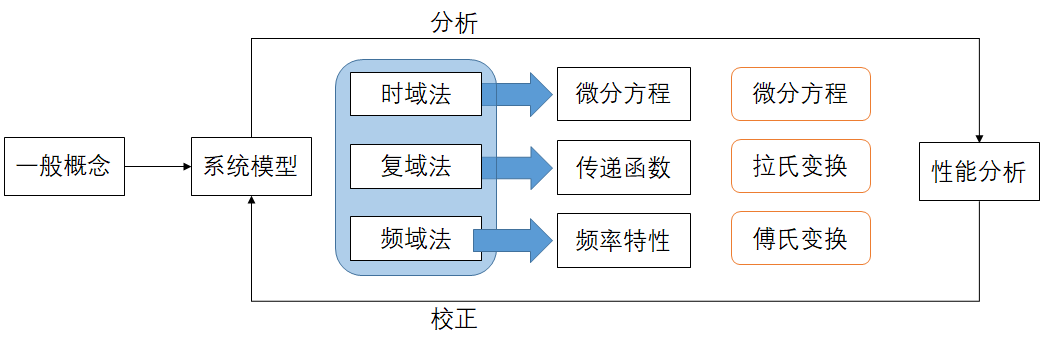
了解数学模型的概念，自动控制原理都包含哪些数学模型，怎样将系统转换为数学模型

什么是控制系统的数学模型？控制系统的模型有哪些种？

数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。

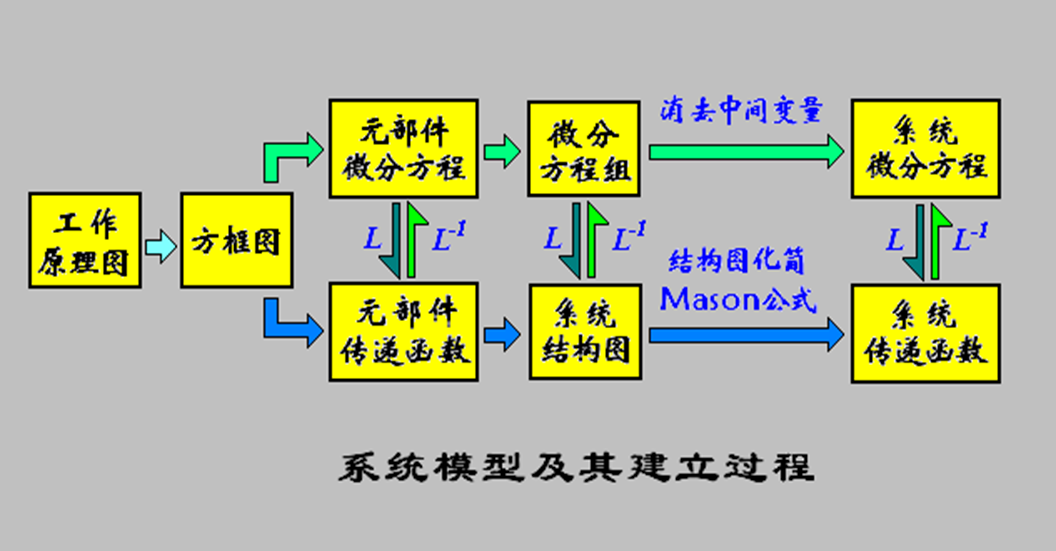
什么是控制系统的数学模型？控制系统的模型有哪些种？

数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。

系统数学模型建立的过程：

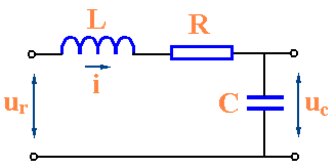
RLC电路微分方程的建立（二阶）

u r ( t ) = L d i ( t ) d t + R i ( t ) + u c ( t ) i ( t ) = C d u c ( t ) d t u r ( t ) = L C d 2 u c ( t ) d t 2 + R C d u c ( t ) d t + u c ( t ) u_r(t)=L\frac{d_i(t)}{dt}+R_i(t)+u_c(t)\\ i(t)=C\frac{du_c(t)}{dt}\\ u_r(t)=LC\frac{d^2u_c(t)}{dt^2}+RC\frac{du_c(t)}{dt}+u_c(t) ur​(t)=Ldtdi​(t)​+Ri​(t)+uc​(t)i(t)=Cdtduc​(t)​ur​(t)=LCdt2d2uc​(t)​+RCdtduc​(t)​+uc​(t) 整理得： d 2 u c ( t ) d t 2 + R L d u c ( t ) d t + 1 L C u c ( t ) = 1 L C \frac{d^2u_c(t)}{dt^2}+\frac{R}{L}\frac{du_c(t)}{dt}+\frac{1}{LC}u_c(t)=\frac{1}{LC} dt2d2uc​(t)​+LR​dtduc​(t)​+LC1​uc​(t)=LC1​

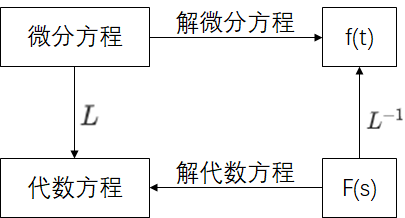
为什么引入拉普拉斯变换？

在自控这门课中，用的最多的自然就是传递函数，谈及传递函数，一个绕不开的一个概念就是：拉普拉斯变换，对于它，我们首先要知道为什么要用到它，这其中有两个原因：

①对于一个系统，如果建立了微分方程，在进行分析时，自然是求解其微分方程，但是过程麻烦，很耗时，所以另辟蹊径。那就是先对微分方程进行拉氏变换得到代数方程，代数方程就很易求解了，对结果再进行拉氏反变换，就可以间接得到微分方程的解。

②可以用拉氏变换定义复域数学模型——传递函数，这是使用它的一个更重要的原因。

直接背会即可，不必采用拉氏变换的几种定理自行证明

此处我们举一个微分方程使用拉氏变求解系统的传递函数的例子 { y ′ ′ ( t ) + a 1 ⋅ y ′ + a 2 ⋅ y ( t ) = 1 ( t ) y ( 0 ) = y ′ = 0 \begin{cases} y^{''}(t)+a_1·y^{'}+a_2·y(t)=1(t) \\ y(0)=y^{'}=0 \end{cases} {y′′(t)+a1​⋅y′+a2​⋅y(t)=1(t)y(0)=y′=0​ 进行 L L L变换 ( S 2 + a 1 S + a 2 ) ⋅ Y ( S ) = 1 S (S^2+a_1S+a_2)·Y(S)=\frac{1}{S} (S2+a1​S+a2​)⋅Y(S)=S1​ 整理得 Y ( S ) = 1 S ( S 2 + a 1 S + a 2 ) R ( S ) = 1 S Y ( S ) R ( S ) = 1 S 2 + a 1 S + a 2 Y(S)=\frac{1}{S(S^2+a_1S+a_2)}\\ R(S)=\frac{1}{S}\\ \frac{Y(S)}{R(S)}=\frac{1}{S^2+a_1S+a_2} Y(S)=S(S2+a1​S+a2​)1​R(S)=S1​R(S)Y(S)​=S2+a1​S+a2​1​

这里附上题目，对拉氏变换进行题目求解

拉氏反变换是重点内容，这里只需要掌握一个公式即可，就是留数法。留数法一般结合查表法使用，因此把一些常用的函数的拉氏变换熟练掌握是十分必要的。

【例题】

【练习】

【例题】

在零初始条件下，线性定常系统输出量拉氏变换与输入量拉氏变换之比。

G ( s ) = C ( s ) R ( s ) G(s)=\frac{C(s)}{R(s)} G(s)=R(s)C(s)​

【例题】

（1）原则上不反映非零初始条件时系统响应的全部信息；

（2）适合于描述单输入/单输出系统；

（3）只能用于表示线性定常系统。