线性回归模型笔记整理1 |
您所在的位置:网站首页 › 线性概率模型系数解释 › 线性回归模型笔记整理1 |
线性回归模型笔记整理1
|
线性回归模型的参数求解
接下来,我们来看一下线性回归模型中的误差。正如我们之前所提及的,线性回归解释的变量(现实中存在的样本),是存在线性关系的。然而,这种关系并不是严格的函数映射关系,但是,我们构建的模型(方程)却是严格的函数映射关系的,因此,对于每个样本来说,我们拟合的结果会与真实值之间存在一定的误差,我们可以将误差表示为:
由于每个样本的误差 ε \varepsilon ε是独立同分布的,根据中心极限定理, ε \varepsilon ε服从均值为0,方差为 σ 2 \sigma ^ {2} σ2的正态分布。 因此,根据正态分布的概率密度公式: 我们所有的样本的权重值都是一样。eg. 不管房间面积是什么,w都是统一的,也就是房的单价都是一样的。w下标没有i ,也是因为对所有样本都一样。 y_hat就是预测值,y是真实值。 每一个样本对应一个不同的误差, 对于每一个样本误差都是不同的。第一个样本的第一个特征,得到一个预测值。 1.2 why 每个样本的误差 ε \varepsilon ε是独立同分布的 ?误差就是加上一个epsilon ,可能是正的,可能是负的,就是一个误差项。误差跟误差之间,都是独立的,每一个样本都是独立的。 eg. 预测房价的时候。一楼的房价与二楼的房价是没有关系的。 误差分布情况是独立的,进行的任务都是同一个任务,同一个任务带来的分布都是同分布的。 服从中心极限定理,指的是随机变量x之间独立同分布,那么这些变量求和就服从正态分布。 误差可能全都预测大吗?有比样本误差大,有比样本误差小的。 这样有多,有少,均值为0 sigma平方,爱是是多少多少。 2. 解释误差的正态分布的概率密度公式:
epsilon = 真实值yi - 预测值y_hat ( 也就是WtXi),带入概率密度公式。 前面是exp,就是常数 e 2.7 epsilon的平方 其实是epsilon - 0的平方,就是减去均值,因为均值为0,底下是2倍 sigma 的平方。 epsilon让它取值非常非常大,之前e的指数图像画过,右边上的越来越快。epsilon误差越来越大。 前面有负号。 exp指数图像就趋向于负的,exp越来越小,exp的负无穷,趋近于 0。准确值概率P越来越小。 epsilon误差不能出现负数,epsilon如果是0,e的0次方就是1,趋向于1 随着epsilon增长 右边 接近于0 变小。我们希望越小越好 那我们换一种方式表达: 左边这块,怎么也变了? 不用纠结于符号,之所以可以变,意义相同 我们希望epsilon 越小越好,epsilon 越小,准确值概率P大 输入xi 输出yi的概率,只有epsilon误差越小 越接近yi。如果误差为0 误差值就和真实值相等。 右侧完全相同,左侧表示 epsilon误差越小 p概率越大 yi ,实际值和预测值y_hat接近, 期望右边的越大,p概率越大,误差越小。 eg. 举骰子的例子。1点到6点,呈均匀分布,这3个骰子都是同分布(均匀分布)。同时,3个骰子之间都是独立,那么这3个骰子点数相加的和服从正太分布。 3粒骰子 求和可能取的值 是3到18。3到18的分布就是正太分布。 骰子点数Why服从正太分布? 穷尽可能: 加入打出 3点 三个骰子都是 1点,打出 18点 三个骰子都是6点,这种组合少。 如果要想打出4点,这种组合就多了 。 如果我们想打出5点,组合更多。 随着点数越来越多,到达中心越来越多,随后降下来。 总而言之,就是两边的可能性最小
注意:用python写也可以,但不如numpy,因为python不能矢量化计算。 取1到6的值,求和sum 最小的是3 到18之间 不可能是0 最后画出图,也可以画直方图。BUT直方图是离散的。关于概率密度图,画连续的最好。所以可视化还是比较有意义的。 # 掷骰子 三粒 取值3-18 # 中心极限定理 # 如果随机变量X (x1, x2, x3.......)是独立分布的,则变量之间的和是服从正太分布的 import numpy as np import pandas as pd result = [] for i in range(10000): array = np.random.randint(1, 7, size=3) result.append(np.sum(array)) s = pd.Series(result) s.plot(kind='kde')
中心极限定理以及其和大数定律的区别 当样本量N逐渐趋于无穷大时,N个抽样样本的均值的频数逐渐趋于正态分布,其对原总体的分布不做任何要求,意味着无论总体是什么分布,其抽样样本的均值的频数的分布都随着抽样数的增多而趋于正态分布
这个正态分布的u会越来越逼近总体均值,并且其方差满足a^2/n,a为总体的标准差,注意抽样样本要多次抽取,一个容量为N的抽样样本是无法构成分布的。 3.2 中心极限定理和大数定律的区别下面援引一段知乎上的回答:https://www.zhihu.com/question/48256489/answer/110106016 大数定律n只要越来越大,我把这n个独立同分布的数加起来去除以n得到的这个样本均值(也是一个随机变量)会依概率收敛到真值u,但是样本均值的分布是怎样的我们不知道。 区分综上所述,这两个定律都是在说样本均值性质。随着n增大,大数定律说样本均值几乎必然等于均值。中心极限定律说,他越来越趋近于正态分布。并且这个正态分布的方差越来越小。 直观上来讲,想到大数定律的时候,你脑海里浮现的应该是一个样本,而想到中心极限定理的时候脑海里应该浮现出很多个样本。 3.3 正态分布的概率密度函数正态分布的概率密度函数均值为μ,方差为σ^2 (或标准差σ)是高斯函数的一个实例:
如果一个随机变量X服从这个分布,我们写作 X ~ N(μ,σ2). 如果μ = 0并且σ = 1,这个分布被称为标准正态分布,这个分布能够简化为 exp,高等数学里以自然常数e为底的指数函数 Exponential |
【本文地址】
今日新闻 |
推荐新闻 |
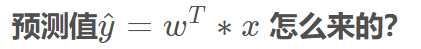 上篇9号博文已经解释过了。
上篇9号博文已经解释过了。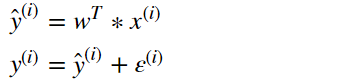 这就是误差值公式。其中,
ε
(
i
)
\varepsilon ^ {(i)}
ε(i)表示每个样本与实际值之间的误差。
这就是误差值公式。其中,
ε
(
i
)
\varepsilon ^ {(i)}
ε(i)表示每个样本与实际值之间的误差。 不能保证所有的预测跟真实值之间都是正确的,因为现实数据也有噪声。
不能保证所有的预测跟真实值之间都是正确的,因为现实数据也有噪声。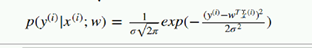 根据
根据 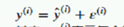 有
有 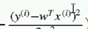
 分号后面的w,表示以w作为参数,后面也有。 前面这个 以 xi作为前提,获取yi的概率。
分号后面的w,表示以w作为参数,后面也有。 前面这个 以 xi作为前提,获取yi的概率。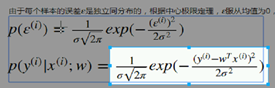 给定xi 期望得到 yi 实际值
给定xi 期望得到 yi 实际值 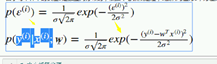 epsilon越小 x(i)越接近实际值y(i)
epsilon越小 x(i)越接近实际值y(i) 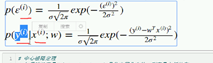


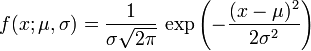
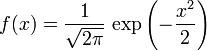 在正态分布中,有一些一些值得注意的量:
在正态分布中,有一些一些值得注意的量: