非线性回归 |
您所在的位置:网站首页 › 线性回归方程做题步骤是什么 › 非线性回归 |
非线性回归
|
非线性回归——非线性函数的最小二乘拟合
非线性回归1.1 可转为线性回归1.2 非线性回归1.2.1 高斯一牛顿法1.2.2 转为最优化问题处理
非线性回归
1.1 可转为线性回归
上一篇文章曲线拟合——最小二乘拟合中已近详细介绍了线性回归的方法。 并且提到了,对于非线性模型中,有3种类型可以线性化:指数方程,幂方程,饱和增长率方程。分别如下: 1.指数方程: y = a 1 e a 2 x y = a_1e^{a_2x} y=a1ea2x 2.幂方程: y = a 1 x a 2 y = a_1x^{a_2} y=a1xa2 2.饱和增长率方程: y = a 1 x x + a 2 y = a_1\frac{x}{x+a_2} y=a1x+a2x 可将其转化为线性形式然后处理。具体方法这里不再细讲,接下来还是主要讲不能线性化的模型的处理方法。 1.2 非线性回归对于不能线性化的模型,我们又该如何处理呢? 以下式为例: y = a 0 ( 1 − e − a 1 x ) y = a_0(1-e^{-a_1x}) y=a0(1−e−a1x) 如果给定一组数据 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . , ( x n , y n ) (x_1,y_1),(x_2,y_2),(x_3,y_3),...,(x_n,y_n) (x1,y1),(x2,y2),(x3,y3),...,(xn,yn),要拟合上述曲线的形式,我们依然采用残差平方和最小原则,残差平方和计算如下: S r = ∑ i = 1 n [ y i − a 0 ( 1 − e − a 1 x i ) ] 2 S_r = \sum_{i=1}^{n} {[y_i- a_0(1-e^{-a_1x_i})]^2} Sr=i=1∑n[yi−a0(1−e−a1xi)]2 接下来就要注意了,如果我们依然和之前线性回归中一样,将上式 S r S_r Sr分别对系数 a 0 a_0 a0和 a 1 a_1 a1求偏导,然后令其为0,那么得到的方程组将是复杂的非线性方程组,使得求解 a 0 a_0 a0和 a 1 a_1 a1的值十分困难。 因此,我们需要寻求其他的处理办法。 接下来介绍两个思路: 1.高斯一牛顿法(迭代)法。 2.最优化的方法; 1.2.1 高斯一牛顿法上面遇到的一大问题就是要解非线性方程组。那我们能不能想办法避免解非线性方程组呢? 于是就有了如下的高斯一牛顿迭代的方法。 首先,对于非线性函数模型,如 y = a 0 ( 1 − e − a 1 x ) y = a_0(1-e^{-a_1x}) y=a0(1−e−a1x),将非线性方程和数据之间的关系表示为一般形式(如果对下面的表示和处理方法不理解的话,可与“曲线拟合——最小二乘拟合”中“线性回归小结”中所讲的联系起来思考): y = f ( x i ; a 1 , a 2 , . . . , a m ) y = f(x_i;a_1,a_2,...,a_m) y=f(xi;a1,a2,...,am) 或 y = f ( x i ) y = f(x_i) y=f(xi) 在参数值处,将上面的非线性模型围绕参数值以泰勒级数展开,并省略一阶导数后面的项。于是,对于有两个参数的情况有 同时,需要注意: 我们跳出上面说的,求偏导然后求解 a 0 a_0 a0和 a 1 a_1 a1的思路。直接想办法,使残差平方和 S r S_r Sr最小。这样,只要能使残差平方和 S r S_r Sr最小,就能满足残差平方和最小原则,得到的就是我们想要的拟合结果。 这里,我们就可以直接利用最优化的方法,将 S r = ∑ i = 1 n [ y i − a 0 ( 1 − e − a 1 x i ) ] 2 S_r = \sum_{i=1}^{n} {[y_i- a_0(1-e^{-a_1x_i})]^2} Sr=∑i=1n[yi−a0(1−e−a1xi)]2作为目标函数,将其中的 a 0 a_0 a0和 a 1 a_1 a1看作是变量,想办法要使 S r S_r Sr最小,而使 S r S_r Sr最小时的 a 0 a_0 a0和 a 1 a_1 a1的值,就是我们所寻找的结果。 于是此问题就变成了二维无约束最优化问题。我们可以采用多为无约束最优化搜索方法来系统地调整参数 a 0 a_0 a0和 a 1 a_1 a1,使 S r S_r Sr的值达到最小。具体一些方法可参考在另一篇文章"最优化方法笔记2:多维无约束最优化"中有介绍,也可以搜索多维无约束最优化应该有很多介绍的。 |
【本文地址】
今日新闻 |
推荐新闻 |
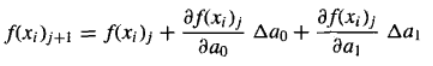 其中,下标为j的是初始参数值(上一次迭代的参数值),下标为j+1的是预测值。
△
a
0
=
a
0
,
j
+
1
−
a
0
,
j
\triangle{a_0}=a_{0,j+1}-a_{0,j}
△a0=a0,j+1−a0,j,
△
a
1
=
a
1
,
j
+
1
−
a
1
,
j
\triangle{a_1}=a_{1,j+1}-a_{1,j}
△a1=a1,j+1−a1,j。 于是,就将原非线性模型关于参数进行了线性化。然后将上式代入到
y
=
f
(
x
i
)
y = f(x_i)
y=f(xi)中,就得到:
其中,下标为j的是初始参数值(上一次迭代的参数值),下标为j+1的是预测值。
△
a
0
=
a
0
,
j
+
1
−
a
0
,
j
\triangle{a_0}=a_{0,j+1}-a_{0,j}
△a0=a0,j+1−a0,j,
△
a
1
=
a
1
,
j
+
1
−
a
1
,
j
\triangle{a_1}=a_{1,j+1}-a_{1,j}
△a1=a1,j+1−a1,j。 于是,就将原非线性模型关于参数进行了线性化。然后将上式代入到
y
=
f
(
x
i
)
y = f(x_i)
y=f(xi)中,就得到: 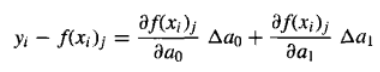 以矩阵形式表示为:
以矩阵形式表示为: 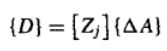

 将线性最小二乘理论应用于式此,得到下面的正规方程:
将线性最小二乘理论应用于式此,得到下面的正规方程: 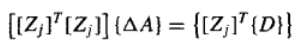 通过求解该线性方程组可得到
△
A
\triangle{A}
△A。然后可以用
△
A
\triangle{A}
△A来计算改进后的参数值:
通过求解该线性方程组可得到
△
A
\triangle{A}
△A。然后可以用
△
A
\triangle{A}
△A来计算改进后的参数值: 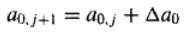 和
和 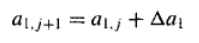 由于泰勒展开并不是精确表示,所以得到的
a
0
a_0
a0和
a
1
a_1
a1并不准确,需要通过重复上面的过程,不断地迭代提高精度,直到求解过程收敛为止,收敛条件:
由于泰勒展开并不是精确表示,所以得到的
a
0
a_0
a0和
a
1
a_1
a1并不准确,需要通过重复上面的过程,不断地迭代提高精度,直到求解过程收敛为止,收敛条件: 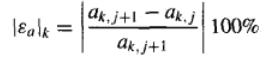 小于一个可以接受的终止条件,结束。
小于一个可以接受的终止条件,结束。