机器学习 |
您所在的位置:网站首页 › 算法分析的主要方面有什么 › 机器学习 |
机器学习
|
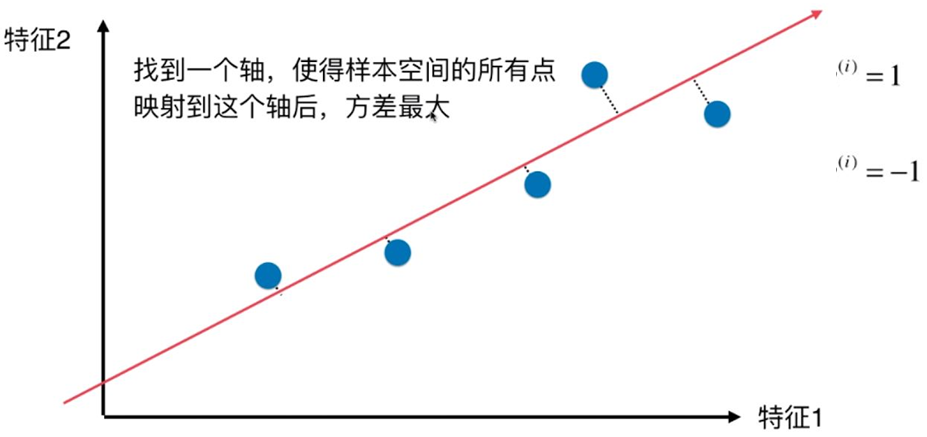
一、PCA算法的原理 PCA(principle component analysis),即主成分分析法,是一个非监督的机器学习算法,是一种用于探索高维数据结构的技术,主要用于对数据的降维,通过降维可以发现更便于人理解的特征,加快对样本有价值信息的处理速度,此外还可以应用于可视化(降到二维)和去噪。 1、PCA与LDA算法的基本思想 数据从原来的坐标系转换到新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,我们可以忽略余下的坐标轴,即对数据进行降维处理。 2、数学推导过程 PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。 求解思路:用方差来定义样本的间距,方差越大表示样本分布越稀疏,方差越小表示样本分布越密集。 方差的公式如下: 在求解最大方差前,为了方便计算,可以先对样本进行demean(去均值)处理,即减去每个特征的均值,这种处理方式不会改变样本的相对分布(效果就像坐标轴进行了移动)。去均值后,样本x每个特征维度上的均值都是0,方差的公式转换下图的公式: 对于只有2个维度的样本,现在的目标就是:求一个轴的方向w=(w1,w2),使得映射到w方向后,方差最大。 目标函数表示如下: 为求解此问题,需要使用梯度上升算法,梯度的求解公式如下: 3、PCA算法流程: (1)去平均值,即每一位特征减去各自的平均值; (2)计算协方差矩阵; (3)计算协方差矩阵的特征值与特征向量; (4)对特征值从大到小排序; (5)保留最大的个特征向量; (6)将数据转换到个特征向量构建的新空间中。 4、PCA算法实现一般流程: (1)对数据进行归一化处理; (2)计算归一化后的数据集的协方差矩阵; (3)计算协方差矩阵的特征值和特征向量; (4)保留最重要的k个特征(通常k要小于n); (5)找出k个特征值相应的特征向量 (6)将m * n的数据集乘以k个n维的特征向量的特征向量(n * k),得到最后降维的数据。 5、PCA降维准则: (1) 最近重构性:样本集中所有点,重构后的点距离原来的点的误差之和最小。 (2) 最大可分性:样本在低维空间的投影尽可能分开。 6、PCA算法优点: (1)使得数据集更易使用; (2)降低算法的计算开销; (3)去除噪声; (4)使得结果容易理解; (5)完全无参数限制。 7、PCA算法缺点: (1)如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高; (2) 特征值分解有一些局限性,比如变换的矩阵必须是方阵; (3) 在非高斯分布情况下,PCA方法得出的主元可能并不是最优的。 8、PCA算法应用: (1)高维数据集的探索与可视化。 (2)数据压缩。 (3)数据预处理。 (4)图象、语音、通信的分析处理。 (5)降维(最主要),去除数据冗余与噪声。 二、代码实现 1.自己实现的PCA算法(不使用sklearn) import numpy as np import matplotlib.pyplot as plt X=np.empty((100,2)) X[:,0]=np.random.uniform(0,100,size=100) X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100) plt.scatter(X[:,0],X[:,1]) def demean(X): return X-np.mean(X,axis=0) X_demean=demean(X) plt.figure(2) plt.scatter(X_demean[:,0],X_demean[:,1]) #print(np.mean(X[:,0])) #print(np.mean(X_deman[:,0])) #print(np.mean(X_deman[:,1])) def f(w,X): return np.sum((X.dot(w)**2))/len(X) def df_math(w,X): return X.T.dot(X.dot(w))*2/len(X) def direction(w): return w / np.linalg.norm(w) def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8): w = direction(initial_w) cur_iter = 0 while cur_iter n: print("k must lower than feature number") return else: #注意特征向量时列向量。而numpy的二维矩阵(数组)a[m][n]中,a[1]表示第1行值 selectVec = np.matrix(featVec.T[index[:k]]) #所以这里须要进行转置 finalData = data_adjust * selectVec.T reconData = (finalData * selectVec) + average return finalData, reconData #输入文件的每行数据都以\t隔开 def loaddata(datafile): return np.array(pd.read_csv(datafile,sep=" ",header=-1)).astype(np.float) def plotBestFit(data1, data2): dataArr1 = np.array(data1) dataArr2 = np.array(data2) m = np.shape(dataArr1)[0] axis_x1 = [] axis_y1 = [] axis_x2 = [] axis_y2 = [] for i in range(m): axis_x1.append(dataArr1[i,0]) axis_y1.append(dataArr1[i,1]) axis_x2.append(dataArr2[i,0]) axis_y2.append(dataArr2[i,1]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(axis_x1, axis_y1, s=50, c='red', marker='s') ax.scatter(axis_x2, axis_y2, s=50, c='blue') plt.xlabel('x1'); plt.ylabel('x2'); plt.savefig("outfile.png") plt.show() #依据数据集data.txt def main(): datafile = "data.txt" XMat = loaddata(datafile) k = 2 return pca(XMat, k) if __name__ == "__main__": finalData, reconMat = main() plotBestFit(finalData, reconMat)运行结果: |
【本文地址】
今日新闻 |
推荐新闻 |
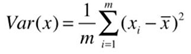
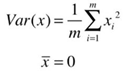 在这里,
在这里,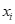 代表已经经过映射后的某样本。
代表已经经过映射后的某样本。