高斯消元法(Gauss Elimination)【超详解&模板】 |
您所在的位置:网站首页 › 稀疏矩阵的逆矩阵例题 › 高斯消元法(Gauss Elimination)【超详解&模板】 |
高斯消元法(Gauss Elimination)【超详解&模板】
|
高斯消元法,是线性代数中的一个算法,可用来求解线性方程组,并可以求出矩阵的秩,以及求出可逆方阵的逆矩阵。高斯消元法的原理是:若用初等行变换将增广矩阵 化为 ,则AX = B与CX = D是同解方程组。 所以我们可以用初等行变换把增广矩阵转换为行阶梯阵,然后回代求出方程的解。 1、线性方程组 1)构造增广矩阵,即系数矩阵A增加上常数向量b(A|b) 2)通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式(triangular form) 注:这里的初等变化可以通过系数矩阵A乘上初等矩阵E来实现 3)从而得到简化的三角方阵组,注意它更容易解 4)这时可以使用向后替换算法(Algorithm for Back Substitution)求解得 z=-4/-4=1, y=4-2z=4-2=2, x= (1-y-z)/2=(1-2-1)/2=-1
总结上面过程,高斯消元法其实就是下面非常简单的过程 原线性方程组 ——> 高斯消元法 ——> 下三角或上三角形式的线性方程组 ——> 前向替换算法求解(对于上三角形式,采用后向替换算法)
补充1: 高斯-若尔当消元法(Gauss-Jordan Elimination)
相对于高斯消元法,高斯-若尔当消元法最后的得到线性方程组更容易求解,它得到的是简化行列式。其转化后的增高矩阵形式如下,因此它可以直接求出方程的解,而无需使用替换算法。但是,此算法的效率较低。
例子如下:
个人感觉区别就是对每行进行了归一化处理 补充2: 介绍了最基本的高斯消元法,现在看看应用于实际问题的实用算法 因为实际应用中,我们总是利用计算机来分析线性系统,而计算机中以有限的数来近似无限的实数,因此产生舍入误差(roundoff error),进而对解线性系统产生很多影响。
一个t位(即精度为t)以 例1:对2位以10为基的浮点算法, 例2:同样考虑
以下面系统为例,看看在高斯消元中采用浮点算法会产生什么效果。 当以精确解法时,通过将第一行乘以m=89/47,并从第二行中减去得到 当以3位以10为基的浮点算法时,乘子变为
尽管无法消除近似误差的影响,可以采用一些技术来尽量减小这类机器误差。部分主元消元法在高斯消元的每一步,都选择列上最大值为轴(通过行变换将其移动)。 下面给出列主元消去的代码(所谓列主元消去法是在系数矩阵中按列选取元素绝对值得最大值作为主元素,然后交换所在行与主元素所在行的位置,再按顺序消去法进行消元。) 1 列选主元消元法 2 /* 3 *Gauss.cpp 4 *功能:列选主元消元法 5 */ 6 #include 7 #include"Gass.h" 8 9 //高斯消元法(列选主元) 10 void Gauss (double a[][MAXNUM],int n) 11 { 12 int i,j; 13 SelectColE(a,n); //列选主元并消元成上三角 14 //回代求解 15 printf("上三角的结果\n"); 16 printM(a,3); 17 for(i=n;i>=1;i--) 18 { 19 for(j=i+1;j matrix[i][j]; 27 } 28 } 29 30 bool inverse ( double ** matrix1, double ** matrix2, const int n ) 31 { 32 int i, j; 33 for ( i = 0; i < n; ++ i )//初始化一个单位矩阵 34 { 35 for ( j = 0; j < n; ++ j ) 36 { 37 if ( i == j ) 38 matrix2[i][j] = 1; 39 else 40 matrix2[i][j] = 0; 41 } 42 } 43 for ( i = 0; i < n; ++i ) 44 { 45 int rowmaxpos = i; 46 for ( j = i + 1; j < n; ++j ) 47 { 48 if ( matrix1[i][j] > matrix1[i][rowmaxpos] ) 49 rowmaxpos = j; 50 } 51 for ( j = i; j < n; ++ j )//按从大到小的顺序排列矩阵 52 { 53 swap( matrix1[j][rowmaxpos], matrix1[j][i]); 54 swap( matrix2[j][rowmaxpos], matrix2[j][i]); 55 } 56 if ( !is_zero(matrix1[i][i]) ) 57 { 58 int divisor = matrix1[i][i]; 59 for ( j = i; j < n; ++ j )//归一化矩阵 60 { 61 matrix1[i][j] /= divisor; 62 matrix2[i][j] /= divisor; 63 } 64 for ( j = i + 1; j < n; ++ j )//高斯消元法处理行列式 65 { 66 int multiple = matrix1[j][i]; 67 for ( int k = i; k < n; ++ k ) 68 { 69 matrix1[i][j] -= matrix1[i][k] * multiple; 70 matrix2[i][j] -= matrix2[i][k] * multiple; 71 } 72 } 73 } 74 else 75 return false; 76 } 77 return true; 78 } 79 80 void output( double ** matrix, const int n ) 81 { 82 for ( int i = 0; i < n; ++i ) 83 { 84 for ( int j = 0; j < n; ++ j ) 85 cout |
【本文地址】
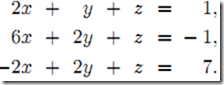


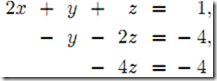


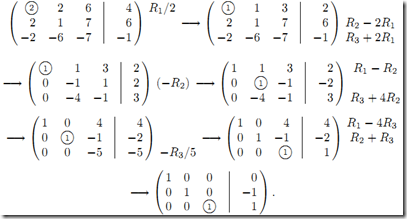 解为
解为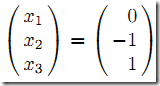
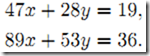
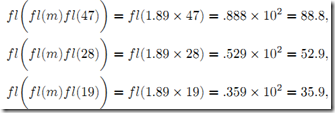 ,因此第一步高斯消元后得
,因此第一步高斯消元后得 。此时,因为不能将第2行第1列位置变为0,所以不能将其三角化。从而,我们只能接受将这个位置值赋为0,而不管其实际浮点值。因此,3位浮点高斯消元的结果为
。此时,因为不能将第2行第1列位置变为0,所以不能将其三角化。从而,我们只能接受将这个位置值赋为0,而不管其实际浮点值。因此,3位浮点高斯消元的结果为 ,后向算法计算结果为
,后向算法计算结果为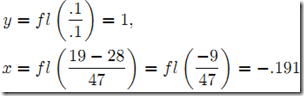 。
。