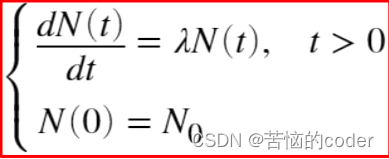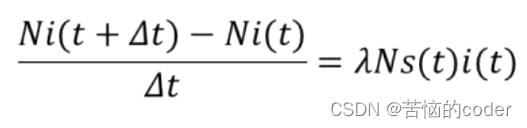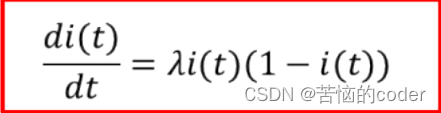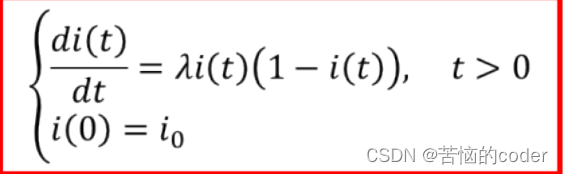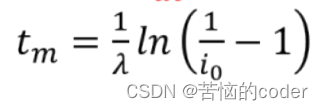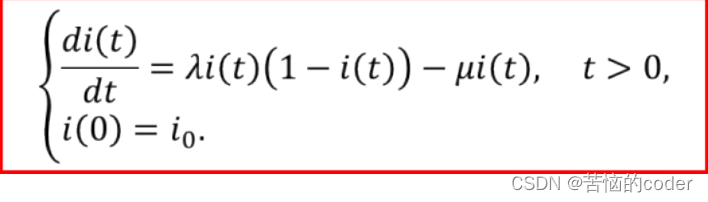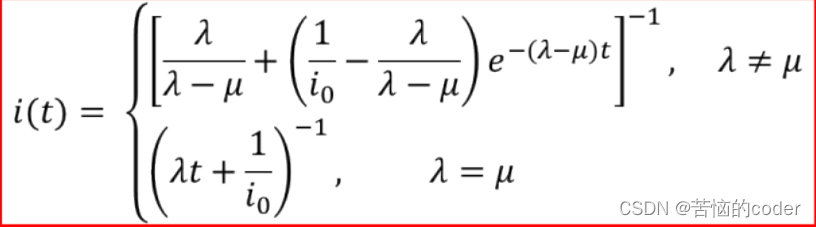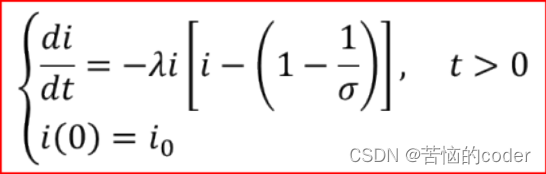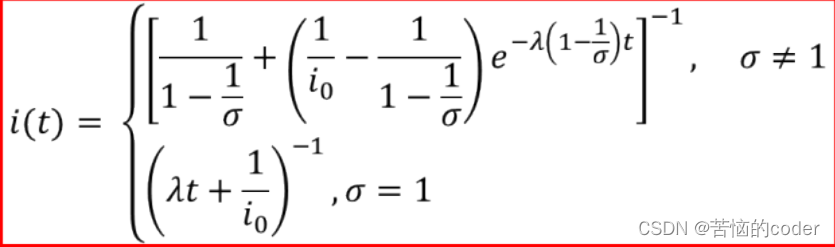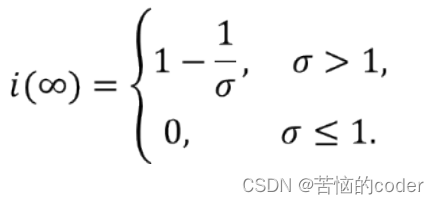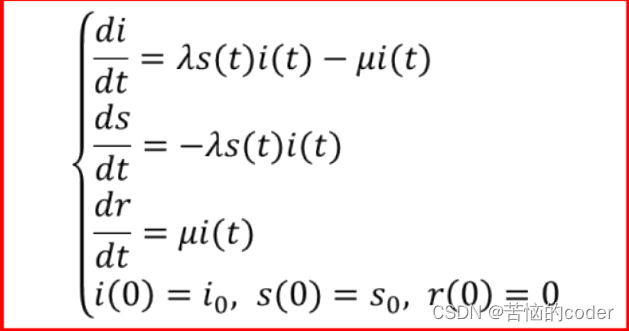|
一、模型简介
传染病预测问题
不同类型的传染病的发病机理和传播途径各有特点有的传染病,在得过一次后可获得免疫力,但有的则不会有的传染病具有潜伏期,有的则没有需要对不同类型的传染病建立相应合适的预测模型
本篇介绍4个不同情况的模型:指数传播模型、SI模型、SIS模型、SIR模型
本篇重点:模型假设与模型改进的思想
二、模型分析
1.指数传播模型
①模型假设
假设所研究的区域是封闭区域,在一定时期内人口总量不变,不考虑迁入和迁出在t时刻患病人数N(t)是随时间连续变化的、可微的函数每个病人在单位时间内会传染到的人数为大于0的常数λ
②模型建立
设N(t)为t时刻患病人数,则t+△t时刻的患病人数为N(t+△t)则从t→t+△t时间内,净增的患病人数为N(t+△t) - N(t)根据假设3(每个病人在单位时间内会传染到的人数为大于0的常数λ),有:N(t+△t) - N(t) = λN(t)△t注意,λ在模型中始终是常数
③微分方程
基于假设2,在N(t+△t) - N(t) = λN(t)△t等号两边同时除以△t,并令△t→0可得微分方程
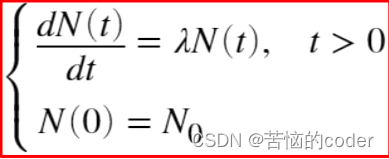
可求得该模型的解析解

④结果分析
该模型显示,患病人数是指数型增长的该模型一般适用于传染病爆发初期因为在初期,传染源和传染途径往往未知,难以防范但是按照模型,t→∞时N(t)→∞,这显然是不符合实际的
⑤模型改进
封闭区域内人数有限,当患病人数越来越多时,健康人群的数量也就越来越少那么单位时间内新增的人数(N(t)的导数)也会减少,毕竟没多少人可以被感染了基于以上分析,对模型进行改进,建立SI模型
2.SI模型
①模型假设
人口总数:所研究的区域内人口总数为常数N,既不考虑生死,也不考虑迁移两类人群:人群分为易感染者(susceptible)和已感染者(infective),设t时刻两类人群在总人口中所占的比例分别为s(t)和i(t),显然s(t) + i(t) = 1日感染率:每个病人在单位时间(每天)内接触的平均人数为常数λ,称为日感染率;当病人所接触的是健康者时,会将其感染成病人不考虑治愈:每个病人得病后会在传染期内无法治愈,且不会死亡
注意事项
现实中,地区人数并不会真的为常数,总有出生率、死亡率、迁入和迁出率等但如果把这些因素考虑进模型,模型会非常复杂;而本题的重心是传染病再次强调模型假设的目的:简化问题
②模型建立和微分方程
细节:假设3中λ是1个病人单位时间接触的平均人数,接触的人中既有病人也有健康者则1个病人单位时间内可使λs(t)个健康者变为病人在t时刻病人总数Ni(t),△t时间内会新增λs(t)Ni(t)△t个病人,则单位时间内新增病人数为
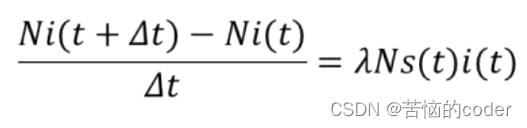
令△t→0,得微分方程

根据假设2,由于s(t) + i(t) = 1,所以可写作
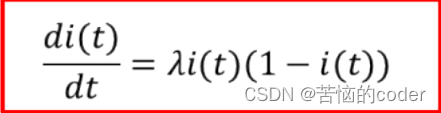
设t = 0时,患病人数占总人口的比例为i(0) = i0,则SI模型:
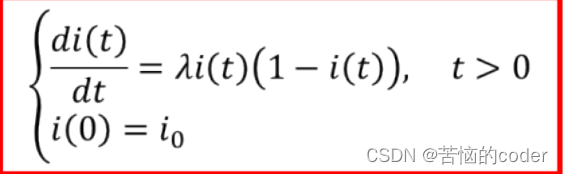
求解该微分方程,得

该模型其实就是Logistic模型,i(t)是病人占总人口的比例,最大值为1,即当t→∞时,区域内所有人都被感染
③结果分析
医学上称di(t)/dt为传染病曲线,表示传染病人增加率与时间的关系,如下图所示
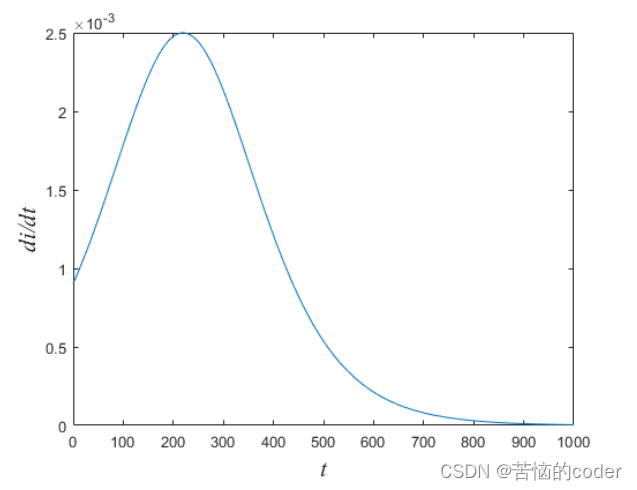
预测结果如下图所示,随着时间的推移,病人比例接近100%当病人总量占总人口比值达到50%,即i = 0.5时,di/dt达到最大值,此时为传染高峰期根据i(t)的表达式,可得高峰期对应时刻
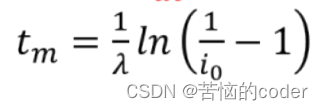
高峰期对应时刻在医学上具有重要意义提前预防:若已知日接触率λ(统计调查等),可预测高峰期到来的时间,做好应对准备由于高峰期时刻与λ成反比,若能减小λ(隔离、戴口罩等),则高峰期时刻将变大也就意味着传染病高峰期来得越晚,现实中可能在高峰期到来之前就彻底解决了该传染病注意:比赛时需要根据数学结果,分析求解结果的现实意义,写进论文
④模型改进
但SI模型中未考虑病人得病后可以治愈,t→∞是i(t)→1,即最后所有人都被感染问题源自模型假设中只有健康者变为病人,但病人不会变为健康者,显然不合理进一步分析问题,可建立SIS模型
3.SIS模型
①模型假设
SIS模型在SI模型假设的基础上,进一步假设
治愈比例:每天被治愈的病人人数占病人总数的比例为μ,且1/μ 为该传染病的平均传染期,即从患病到治愈的天数无免疫性:病人被治愈后成为仍可被感染的健康者
②模型建立和微分方程
由假设可得SIS模型:
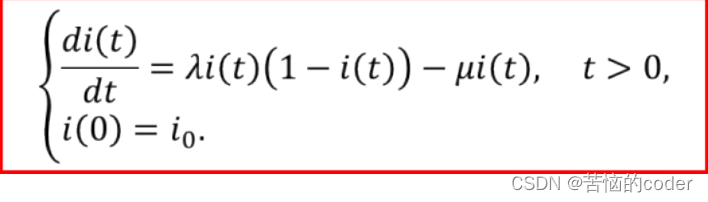
该模型的解析解为:
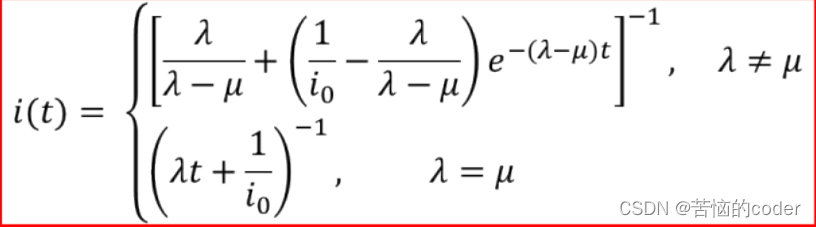
令σ = λ / μ为传染强度,代表的是每个患病者在整个传染期 1/μ 天内,有效接触的易感者人数,即接触数,带入上面的公式,得微分方程和解析解:
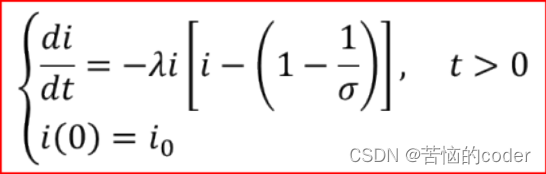
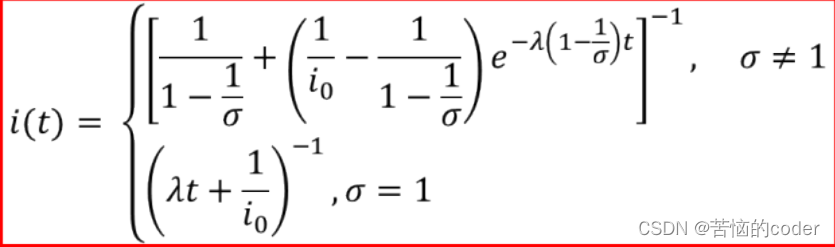
③结果分析
根据解析解,当t→∞时,可得:
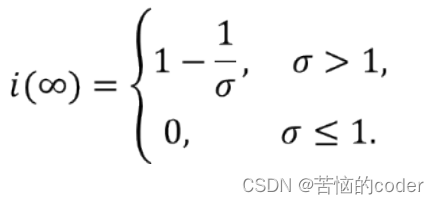
④模型改进
SIS分析是建立在假设“无免疫性:病人被治愈后成为仍可被感染的健康者”的基础上进一步考虑现实中天花、麻疹、流感、肝炎等疾病经治愈后均有很强的免疫力病愈后的人因已具有免疫力,既非易感染者也非病人(已感染者),即这部分人已退出感染系统,再也不会被感染成患者因此,考虑免疫性,改进为SIR模型
4.SIR模型
①模型假设
人群分易感者(susceptible)、病人(infective)和病愈后有免疫力而退出系统的移除者(removal)设任意时刻t,这三类人群占总人口的比例分别为s(t),i(t)和r(t)病人的日接触率为λ,日治愈率为μ人口总数N为固定常数,既不考虑生死,也不考虑迁移
②模型建立
对于全体人群:s(t) + i(t) + r(t) = 1对于移除者:Ndr/dt = μNi(t)对于患者:Ndi/dt = λNs(t)i(t) - μNi(t)对于健康者:Nds/dt = -λNs(t)i(t)
则有
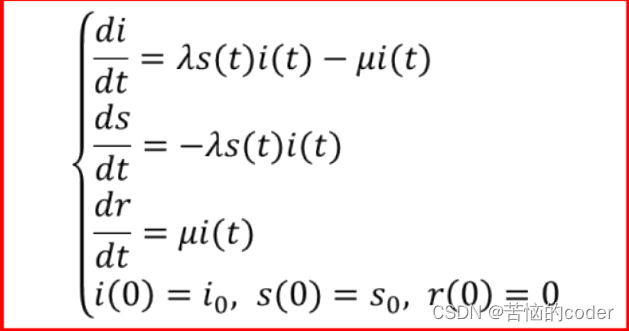
③模型分析
SIR模型形式是多个相互关联的系统变量之间的常微分方程组,属于典型的系统动力学模型更复杂的情况,考虑有些传染病具有潜伏期,考虑一类人为潜伏者,建立SEIR模型类似的问题:河流各类污染物质的耗氧、复氧、吸附、沉降等该类问题往往难以求得精确的解析解,可以使用MATLAB求数值解
|