一文看懂测量的误差与估读 |
您所在的位置:网站首页 › 电表读数估读方法视频教程 › 一文看懂测量的误差与估读 |
一文看懂测量的误差与估读
|
为什么实验仪器吭哧吭哧测量出来的数据要估读?为什么对象被同一个实验仪器多次测量取其平均值就会靠谱一些?该死的估读到底怎么弄?问题三连!!!
一、误差 把测量值与被测对象的真实值的差值称为测量的误差。 误差测量值真实值 估读的原因想必大家都知道,任何测量都有误差。因为你想测量就得借助测量工具,首先工具的制作就允许存在一定的误差;而使用工具的人、使用工具时的环境与条件都不可避免地带来误差。可以这么说,很多真实值你是压根没法知道的,测出来的永远都是不准确的值。即使有些真实值你知道,比如平面上的圆周角是360度,可是你的量角器是无法避免误差的。所以,就算天王老子来了,误差还是如影随形,相伴如故。与其纠结得不到真实值,不如把精力花在如何减小误差上。在高中物理的实验里,会遇到两种类型的误差,也就是熟知的系统误差和随机误差。系统误差就是相同条件的多次测量下,你的测量值相比真实值总是偏大(小)或者按某种规律变化。比如一把没校准的枪按照正常的瞄准姿势射击,弹着点肯定是偏向目标的某一侧,这就是系统误差。而随机误差就是相同条件的多次测量下,你的测量值与真实值的差值没有规律的变化。数理统计里有个著名的‘随机游走’例子,说的就是一个醉汉在广场上完全无意识的行走,他的下一步往哪个方向走你根本没法预料。
这就是一个典型的随机误差的例子 其实这两类误差也不是泾渭分明的,在一定条件下两者是可以转换的。比如你拿着一把尺子量长度,要是事先知道这把尺子有问题,那么测量出来的结果你肯定会归为系统误差;如果你以为这是一把标准尺子,那么测量结果你就会认为是随机误差(反正结果都偏大(小),你也不知道嘛)。 在高中物理的实验里,排除仪器自身的问题外,出现系统误差的原因主要就是实验方案了,比如探究力、加速度和质量关系的方案,电表的内外接法,伏安法测电源的电动势与内阻等,这种情况通过更换实验方案可以解决。这里只说随机误差怎么处理。 二、算术平均值靠谱? 想必大家都知道对同一对象多次测量取其算术平均值就能很好的减小随机误差。不过在历史上这个观念可曾备受质疑,为啥呢?这得从误差的认识说起。 据悉是伽利略首次提出了观测误差(就是随机误差的意思),他在其著作《关于两个主要世界体系的对话——哥白尼与托勒密的》中就写道:1、所以观测都会有误差,其来源归因于观测者、仪器和观测条件。2、观测误差对称的分布在0的两侧(从这里就能看出他指的是随机误差)。3、小误差比大误差出现得更频繁。 虽然人们认识到了误差,那么观测结果怎么取呢?在伽利略时代,天文观测进行得如火如荼,那些天文界的大佬们觉得应该‘谨慎的选择观察值’——即‘择优选择’。因为他们担心那些不好的观察数据会影响好的观察结果,就好比和稀泥一样。但是这种做法也备受质疑——设备不同、观测人员的素质不同、观测条件不同,谁才是翘楚呢? 另外,随机误差是不是真的有这样的分布特点?对于这些疑问,后续有的是数学家在接力研究,直到大boss高斯给其盖棺定论了。
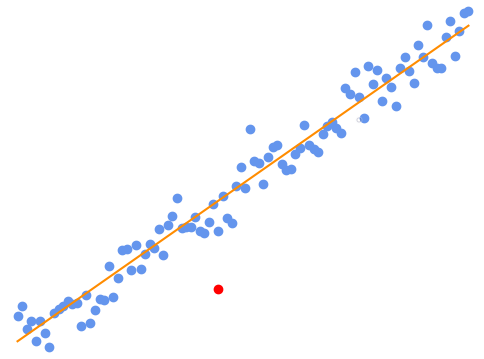
这就从数学上证明了对多次测量结果取算术平均值的效果要好。 到这里,我们只是找到了一种衡量办法(最小二乘法)发现了算术平均值的优点。而高斯的贡献就在于他把随机误差的常见分布特点给找出来——大名鼎鼎的正态分布!顺带着还给上述的衡量办法以正名,给予了它名正言顺的统计意义。有了理论武器做保证,对于测量数据的处理也更上一个台阶了。线性回归就是一个重要的工具。当大量测量数据如下图所示分布时,可以找到一条最优的倾斜直线来拟合数据分布的特点。一旦获得了这条倾斜直线的信息,也就揭开了测量数据的神秘面纱。
是不是想起了被描点作图支配的恐惧? 取平均值虽好,但是万一测量结果里有些刺头儿怎么办?比如上图里的这个红点就明显不合群,要是直接把它拿去和其他结果求平均值,结果肯定会有很大的偏差。这就好比把富豪的收入与我的收入求平均,我立马就财富自由了。喂,醒醒,继续码字啦...遇到这种情况时,若发现是数据记录有误或者实验条件发生了变化等,意味着这个数据偏离了群众路线,革它的命就是了。否则就得仔细分析一下是不是有啥新发现。三、怎么估读呢? 根据误差理论,读数的表示方式为: 读数且读数的最后一位要与仪器误差 的出现位对齐,即仪器误差出现在哪一位,那么就估读到哪一位。 在高中范围内使用的常见各种仪器,一般按照其最小分度值的一半作为最大仪器误差。刻度尺
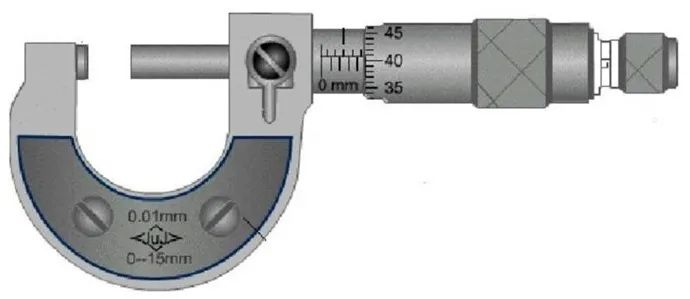
螺旋测微器
螺旋部分的最小分度是0.01mm。按照‘半格误差’来算,则仪器误差为0.005mm,所以仪器误差出现的位置为0.001mm。显然它也是十分法估读。读数的结果就是小数后面取三位(以mm为单位)。比如2.225mm,5.640mm。最后一位小数都是估读的,也是有效的。 弹簧秤
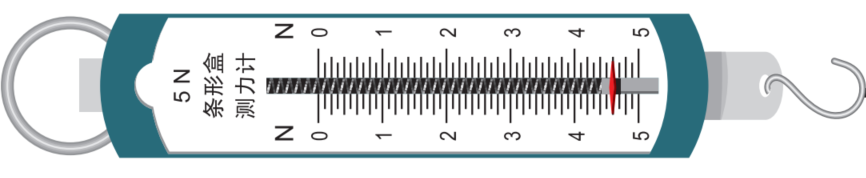
这个弹簧秤的最小分度是0.05N。按照‘半格误差’来算,则仪器误差为0.025N,由于误差值只取一位有效数字,所以仪器误差出现的位置为0.01N。由于误差位数为最小分度的五分之一,故称为五分法估读。读数的结果就是小数后面取两位(以N为单位)。比如0.32N,1.15N。最后一位小数都是估读的,也是有效的。
这个弹簧秤的最小分度是0.1N。按照‘半格误差’来算,则仪器误差为0.05N,所以仪器误差出现的位置为0.01N。这种情况下是十分法估读。读数的结果就是小数后面取两位(以N为单位)。比如0.32N,1.15N。最后一位小数都是估读的,也是有效的。 对比这两个弹簧秤的读数,同样是1.15N,上面这个弹簧秤的5要更准确,因为有对应的刻度。而对于下面的弹簧秤来说,5就是人为大致判断的。
电流表
电压表
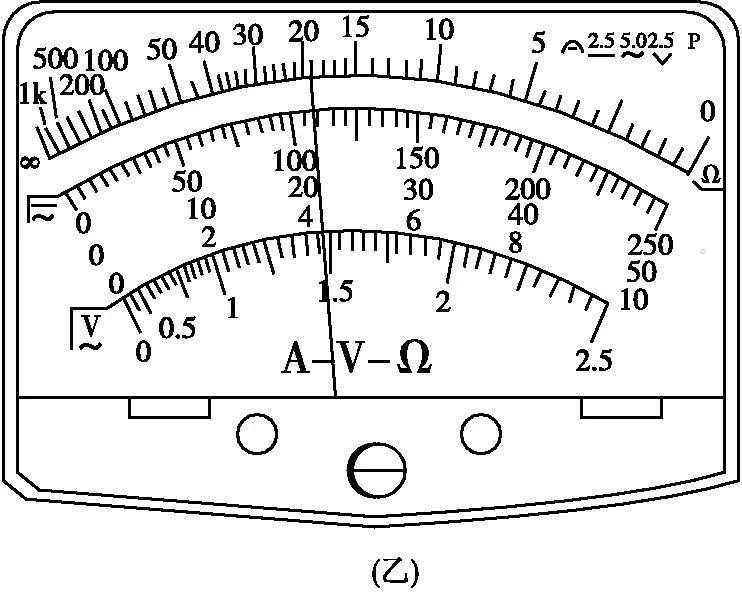
多用电表欧姆档
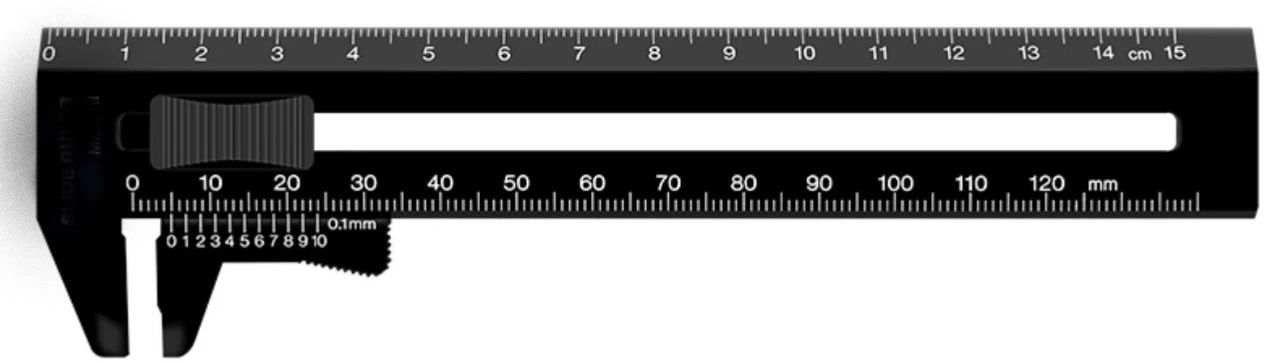
欧姆表(多用电表的欧姆档)的原理决定了其刻度是不均匀的,根据表盘刻度的分布特点,选择分段判断其仪器误差出现的位数,从而采取对于的估读办法。(该法同样参见文末给出的论文) 0—5Ω的刻度范围,最小分度值为0.5Ω。仪器误差为0.25Ω,只取一位有效数字,所以仪器误差出现的位置为0.1Ω,故此段刻度范围内用五分法估读。读数的结果就是小数后面取一位(以Ω为单位)。比如3.1Ω,2.5Ω。5—20Ω的刻度范围内,最小分度值为1Ω,仪器误差为0.5Ω,仪器误差出现的位置为0.1Ω,故此段刻度范围内用十分法估读。读数的结果就是小数后面取一位(以Ω为单位)。比如6.4Ω,12.8Ω。20~40Ω的刻度范围内,最小分度值为2Ω,仪器误差为1Ω,仪器误差出现的位置为1Ω,故此段刻度范围内用二分法估读。读数的结果就是不取小数(以Ω为单位)。比如24Ω,36Ω。再往后,最小分度值越来越大,也意味着读数的精度越来越低,所以需要换挡测量了。最后再来看看游标卡尺,它算是一个异类,其仪器误差不是最小分度值的一半。常见的分度值为0.1mm、0.05mm和0.02mm,根据国家标准,不同分度值对应的仪器误差分别为0.1mm、0.05mm和0.02mm。即仪器误差出现的位置分别为0.1mm、0.01mm和0.01mm,分度值与与仪器误差出现的位数相同。
所以游标卡尺的估读采取就近读刻度的原则——哪怕游标尺上没有任何一条刻度与主尺刻度完全对齐,也应该选择游标尺上与主尺刻度靠得最近的那条刻度来读数。由于游标卡尺的读数规则是:主尺的准确读数+对齐条数*最小分度值,而对齐条数没有按照前面常见仪器那样估读,所以就造成了游标卡尺不需要估读的说法。 以上常见仪器都是属于可连续读出数据的情形。对于机械停表和电阻箱来说,它俩是依靠齿轮转动来工作的,不存在转半格齿轮的情况,所以它们的读数本就是不连续的,因此不用估读。如今得益于传感器的普及,各种电子测量仪器随处可见,其显示的数据已经经过了数字电路的处理,也用不着去估读了。四、写在最后或许再经过若干年的发展,现有的学生实验仪器都会普及电子化,读数问题不再上得来台面,就像如今算盘的地位一样。但是对待准确实验数据的态度依旧是起码的物理素养,所以别去幻想可以逃避如何正确地读数哟。 参考文献[1]陈希孺.数理统计学简史[M].长沙:湖南教育出版社,2000.[2]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004.[3]何志强,王笑君.从误差理论看中学常见测量仪器的估读[J].物理教师,2014,35. |
【本文地址】