图神经网络的下游任务1 |
您所在的位置:网站首页 › 用来表示xml中节点的是什么 › 图神经网络的下游任务1 |
图神经网络的下游任务1
|
图神经网络的下游任务1-利用节点特征进行节点分类
引言
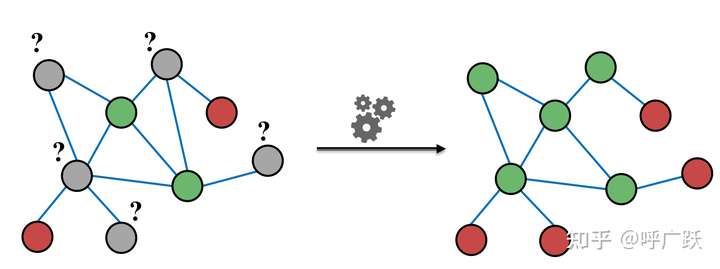
之前提到(先挖个坑,后面补上更详细的关于图神经网络的特点、分类及应用的博客链接)图神经网络根据学习到不同的特征,可以进行不同的下游任务,如下表所示: 图神经网络输出的特征 下游任务 应用 节点特征 节点分类、节点聚类 词向量学习、商品/好友推荐、实体识别...... 连边特征 链路预测 路况预测、商品推荐....... 图级别特征 图分类、图聚类 文本分类、新药物的发现、化合物筛选、蛋白质相互作用点检测......本文就将介绍如何利用图神经网络学习节点特征并进行节点分类任务,看完后应该可以回答以下几个问题: 节点分类任务是什么? 节点分类的基本步骤? 有什么方法可以学习图中的节点特征? 如何利用图神经网络学习图中的节点特征? 如何利用图神经网络学习到的节点特征进行节点分类任务? 节点分类任务&步骤 节点分类定义根据节点的属性(可以是类别型、也可以是数值型)、边的信息、边的属性(如果有的话)、已知的节点预测标签,对未知标签的节点做类别预测。
图中节点特征的学习时图嵌入任务的一个部分。图嵌入(Graph Embedding/Network Embedding,GE)的概念,这里直接摘抄引用知乎大佬(@苘郁蓁)的回答:一文读懂图卷积GCN: 图嵌入(Graph Embedding/Network Embedding,GE),属于表示学习的范畴,也可以叫做网络嵌入,图表示学习,网络表示学习等等。通常有两个层次的含义: 将图中的节点表示成低维、实值、稠密的向量形式,使得得到的向量形式可以在向量空间中具有表示以及推理的能力,这样的向量可以用于下游的具体任务中。例如用户社交网络得到节点表示就是每个用户的表示向量,再用于节点分类等; 将整个图表示成低维、实值、稠密的向量形式,用来对整个图结构进行分类;图嵌入的方式主要有三种: 矩阵分解:基于矩阵分解的方法是将节点间的关系用矩阵的形式加以表达,然后分解该矩阵以得到嵌入向量。通常用于表示节点关系的矩阵包括邻接矩阵,拉普拉斯矩阵,节点转移概率矩阵,节点属性矩阵等。根据矩阵性质的不同适用于不同的分解策略。 DeepWalk:DeepWalk 是基于 word2vec 词向量提出来的。word2vec 在训练词向量时,将语料作为输入数据,而图嵌入输入的是整张图,两者看似没有任何关联。但是 DeepWalk 的作者发现,预料中词语出现的次数与在图上随机游走节点被访问到底的次数都服从幂律分布。因此 DeepWalk 把节点当做单词,把随机游走得到的节点序列当做句子,然后将其直接作为 word2vec 的输入可以节点的嵌入表示,同时利用节点的嵌入表示作为下游任务的初始化参数可以很好的优化下游任务的效果,也催生了很多相关的工作; Graph Neural Network:图结合deep learning方法搭建的网络统称为图神经网络GNN,也就是下一小节的主要内容,因此图神经网络GNN可以应用于图嵌入来得到图或图节点的向量表示;其中矩阵分解和DeepWalk都是无监督的图嵌入方式。 上述内容很好地表述了图嵌入和图神经网络的关系。 此外,在利用数据进行图神经网络时,其中一个输入参数为节点特征,也就是节点的初始特征。如果节点初始特征未知的话,我们可以依靠以上的知识推测,至少有两种方案获取节点初始特征: 基于矩阵分解:分解节点邻接矩阵获取节点初始特征; 基于DeepWalk+word2vec:利用图进行deep walk,再输入word2vec生成节点初始特征; 此外,深度学习新星 | 图卷积神经网络(GCN)有多强大? 中提到,还可以: 将节点数量大小的单位矩阵作为节点的初始特征。 利用图神经网络进行节点分类任务根据之前博客[GNN环境配置和PyG库的使用 | 冬于的博客 (ifwind.github.io)]中提到的最简单的图神经网络构建流程,在这篇博客中先总结如何用PyG提供的封装好的接口设计网络学习节点特征的和进行节点分类,具体每个封装层的原理暂时不深究。 同时,让我们利用PyG自带的数据集进行实验,也就是说,我们也暂时跳过了“继承Data类设计数据加载类”这一步,只设计了下图中红色方框中的代码。  最简单的GNN构建流程图
数据集介绍 最简单的GNN构建流程图
数据集介绍
PyG内置了大量常用的基准数据集,以PyG内置的Planetoid数据集为例。Planetoid数据集类的官方文档为torch_geometric.datasets.Planetoid。 我们在这里使用的是其中的Cora 数据,数据加载代码如下: PS.若出现下载连接超时的情况可以参考《Planetoid无法直接下载Cora等数据集的3个解决方式》进行解决。 加载数据 from torch_geometric.datasets import Planetoiddataset = Planetoid(root='dataset/Cora', name='Cora')#包括数据集的下载,若root路径存在数据集则直接加载数据集data = dataset[0] #该数据集只有一个图len(dataset):1# Data(edge_index=[2, 10556], test_mask=[2708],# train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])该数据包含 2708 篇科学出版物(节点),总共分为7类。引文网络由 5429 个引用链接(边)组成。数据集中的每个出版物都由一个 0/1 值的词向量描述,指示字典中相应词的缺失/存在。该词典由 1433 个独特的词组成,相对于一个one hot编码的词袋向量,此向量为节点的初始特征向量(data.x,维度为[2708,1433])。训练数据为120个带类别标签的节点,测试数据为1000个未标记的节点。 实验前面提到,节点分类任务是根据已知类别标签的节点和节点特征的映射,对未知类别标签节点进行类别标签标注。事实上仅仅利用Cora数据中节点的初始特征向量信息,将它们扔进分类器就可以进行节点分类了。 设计了3个模型(多层感知机、基于GCNConv的图卷积神经网络GCN、基于TransformerConv的模型)分别进行对比,其中多层感知机只利用了节点特征,而GCN利用了节点自身属性与周围邻居节点的属性,基于TransformerConv的模型考虑了不同邻居对节点自身属性的不同影响。 设计Net MLP多层感知机设计这个MLP为两个线性(Linear)层、一个ReLU非线性层和一个dropout操作。第一个Linear层将1433维的特征向量嵌入(embedding)到低维空间中(hidden_channels=16),经过ReLU层激活,再经过dropout操作,输入第二个Linear层——将低维节点表征嵌入到类别空间中(num_classes=7)。 import torchfrom torch.nn import Linearimport torch.nn.functional as F#设计Netclass MLP(torch.nn.Module): def __init__(self, hidden_channels): super(MLP, self).__init__() torch.manual_seed(12345) #设定随机种子,可省略 self.lin1 = Linear(dataset.num_features, hidden_channels) self.lin2 = Linear(hidden_channels, dataset.num_classes) def forward(self, x): x = self.lin1(x) x = x.relu() x = F.dropout(x, p=0.5, training=self.training) x = self.lin2(x) return xmodel = MLP(hidden_channels=16)print(model)#MLP(# (lin1): Linear(in_features=1433, out_features=16, bias=True)# (lin2): Linear(in_features=16, out_features=7, bias=True)#) 基于GCNConv的模型设计这个GCN网络为两个GCNConv层、一个ReLU非线性层和一个dropout操作。第一个GCNConv层将1433维的特征向量嵌入(embedding)到低维空间中(hidden_channels=16),经过ReLU层激活,再经过dropout操作,输入第二个GCNConv层——将低维节点表征嵌入到类别空间中(num_classes=7)。 值得注意的是,在forward()函数中输出的是节点特征,维度为[2708,7],而不是输出经softmax层的分类概率。 import torchfrom torch_geometric.datasets import Planetoidimport torch.nn.functional as Ffrom torch_geometric.nn import GCNConv#设计Netclass GCN(torch.nn.Module): #初始化 def __init__(self, hidden_channels): super(GCN, self).__init__() torch.manual_seed(12345) self.conv1 = GCNConv(dataset.num_features, hidden_channels) self.conv2 = GCNConv(hidden_channels, dataset.num_classes) #前向传播 def forward(self, x, edge_index): x = self.conv1(x, edge_index) x = x.relu() x = F.dropout(x, p=0.5, training=self.training) x = self.conv2(x, edge_index) #注意这里输出的是节点的特征,维度为[节点数,类别数] return x#实例化模型model = GCN(hidden_channels=16)print(model)#GCN(# (conv1): GCNConv(1433, 16)# (conv2): GCNConv(16, 7)#) 基于TransformerConv的模型特别地,通过更换卷积层,我们可以得到基于其他卷积层的模型,卷积层API可参考:torch_geometric.nn-convolutional-layers
比如将GCNConv更换为TransformerConv,来实现基于TransformerConv的图节点分类神经网络。不同卷积层的输入参数不同,详见各卷积层API。 class Transformer(torch.nn.Module): #初始化 def __init__(self, hidden_channels): super(Transformer, self).__init__() torch.manual_seed(12345) self.conv1 = TransformerConv(dataset.num_features, hidden_channels,dropout=0.5) #GCNConv更换为TransformerConv self.conv2 = TransformerConv(hidden_channels, dataset.num_classes,dropout=0.5)#GCNConv更换为TransformerConv #前向传播 def forward(self, x, edge_index): x = self.conv1(x, edge_index) x = x.relu() x = F.dropout(x, p=0.5, training=self.training) x = self.conv2(x, edge_index) #注意这里输出的是节点的特征,维度为[节点数,类别数] return x 选择优化器我们这里选择Adam优化器,如何选择优化器可以参考: 机器学习:各种优化器Optimizer的总结与比较 优化器怎么选?一文教你选择适合不同ML项目的优化器 机器学习项目中该如何选择优化器 pytorch中的优化器,可参考torch.optim。 将该模型中可优化的参数model.parameters()注册到优化器中,lr为学习率,weight_decay为学习率衰减系数。之后在训练过程中利用optimizer.step()更新参数。 #选择优化器optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4) 选择loss function我们选择交叉熵(CrossEntropy)作为loss function,其他loss function见torch.nn-loss function,如何选择loss function参考深度学习中常见的激活函数与损失函数的选择与介绍: criterion = torch.nn.CrossEntropyLoss()因为CrossEntropyLoss()中做了softmax相关操作,所以在设计网络时,只需要直接输出节点的特征。 torch.nn.CrossEntropyLoss()源码截取: #....return nll_loss(log_softmax(input, 1), target, weight, None, ignore_index, None, reduction)将模型输出的维度设计成节点类别的个数,在利用loss function引导模型进行节点特征学习时,正确标签的的概率越大,loss越小。 训练模型model.train()开启模型的训练模式,由于数据集较小,没有分batch训练(直接作为1个batch),经: 梯度置零 模型前向传播 计算loss 反向传播 优化器梯度下降完成一个epoch的训练。 关于Epoch, Batch, Iteration的区别可以参考:深度学习 | 三个概念:Epoch, Batch, Iteration #训练函数def train(model,data,optimizer,criterion): model.train() optimizer.zero_grad() # 梯度置零 out = model(data.x, data.edge_index) # 模型前向传播 loss = criterion(out[data.train_mask],data.y[data.train_mask]) # 计算loss loss.backward() # 反向传播 optimizer.step() # 优化器梯度下降 return loss#训练for epoch in range(1, 201): loss = train(model,data,optimizer,criterion) print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}') 测试model.eval()开启模型的测试模式,利用训练好模型中的各层权重矩阵聚合各层邻居节点的消息,预测目标结点的特征。 #测试函数def test(model,data): model.eval() out = model(data.x, data.edge_index) pred = out.argmax(dim=1) # 使用最大概率的类别作为预测结果 test_correct = pred[data.test_mask] == data.y[data.test_mask] # 获取正确标记的节点 test_acc = int(test_correct.sum()) / int(data.test_mask.sum()) # 计算正确率 return test_acc#精度评价test_acc = test(model,data)print(f'Test Accuracy: {test_acc:.4f}') 可视化我们可以直接利用模型输出的节点特征降维进行可视化,用TSNE降维方法将节点特征降至2维,在坐标系中可视化。 import matplotlib.pyplot as pltfrom sklearn.manifold import TSNE#可视化def visualize(out, color): z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy()) plt.figure(figsize=(10,10)) plt.xticks([]) plt.yticks([]) plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2") plt.show() model.eval()out = model(data.x, data.edge_index)visualize(out, color=data.y) 实验结果 分类精度&可视化结果 模型 精度 MLP 0.5900 基于GCNConv的模型
0.8140
基于GCNConv的模型
0.8140
 基于TransformerConv的模型
0.7900
基于TransformerConv的模型
0.7900

由前述代码的实验结果可以发现节点分类精度:MLP模型 |
【本文地址】
今日新闻 |
推荐新闻 |