在物理学里，理想刚体（rigid body） 是一种有限尺寸，可以忽略形变的固体。不论是否感受到外力，在刚体内部，质点与质点之间的距离都不会改变[1]^{[1]}[1]。

对于刚体来说，总共有 666 个自由度，其中 333 个为平动自由度，333 个为转动自由度。一般的刚体运动就对应这六个自由度。如果对这些自由度再进行一些限制，那么会得到一些特殊的运动模式。

按照自由度的数目，我们分为：

其中最基本的操作是刚体的转动与平动。

平动可以用质心位移 (x,y,c)(x,y,c)(x,y,c) 来描述，对于转动来说。我们可以通过固定在刚体上的坐标系（本体坐标系）的转动来描写[2]^{[2]}[2]。考虑本体坐标系的三个正交基矢为 {i,j,k}\{\bm{i},\bm{j},\bm{k}\}{i,j,k}，通过转动操作后，基矢变为 {i′,j′,k′}\{\bm{i}',\bm{j}',\bm{k}'\}{i′,j′,k′}，这可以用下列式子表示：

(i′j′k′)=U(ijk)(1)\begin{pmatrix} \bm{i}'\\ \bm{j}'\\ \bm{k}'\\ \end{pmatrix} = U \begin{pmatrix} \bm{i}\\ \bm{j}\\ \bm{k}\\ \end{pmatrix}\tag{1} ⎝⎛​i′j′k′​⎠⎞​=U⎝⎛​ijk​⎠⎞​(1)

其中 UUU 为一个正交矩阵。由此，我们可以使用 UUU 去表征这个转动操作。一个3×33\times 33×3 的正交矩阵只有 333 个独立变量，正好对应 333 个转动自由度。反过来，任意一个 3×33\times 33×3正交矩阵必定对应一个转动操作。这意味着多个连续进行的转动操作 UiU_iUi​ 都可以使用一个转动操作 U=Un⋯U1U = U_n\cdots U_1U=Un​⋯U1​ 代替：

UTU=(Un⋯U1)TUn⋯U1=U1T⋯UnTUn⋯U1=1(2)\begin{aligned} U^T U &= (U_n\cdots U_1)^TU_n\cdots U_1\\ & = U_1^T\cdots U_n^TU_n \cdots U_1\\ & = 1 \end{aligned}\tag{2} UTU​=(Un​⋯U1​)TUn​⋯U1​=U1T​⋯UnT​Un​⋯U1​=1​(2)

欧拉转动定理 告诉我们，对于任意一个转动操作 UUU，均存在一根轴 n^\hat{\bm{n}}n^ 使得：

Un^=n^(3)U \hat{\bm{n}} = \hat{\bm{n}}\tag{3} Un^=n^(3)

此时 n^\hat{\bm{n}}n^ 就是 UUU 的本征值为 111 的本征向量。为此我们只要证明 111 是 UUU 的一个本征值，那么 (3)(3)(3) 式自然得证。我们有：

det⁡(U−I)=det⁡(U−UUT)=det⁡Udet⁡(I−UT)=det⁡(I−U)T=det⁡(I−U)=(−1)3det⁡(U−I)\begin{aligned} \det (U-I) & =\det (U-UU^T)\\ & = \det{U}\det(I-U^T)\\ & = \det (I-U)^T\\ & = \det (I-U) \\ & = (-1)^3 \det(U-I) \end{aligned} det(U−I)​=det(U−UUT)=detUdet(I−UT)=det(I−U)T=det(I−U)=(−1)3det(U−I)​

于是得到：

det⁡(U−I)=0\det (U-I) = 0 det(U−I)=0

得证

因此，任意一个转动操作都可以看作绕一根轴 n^\hat{\bm{n}}n^ 转动一定角度 ϕ\phiϕ 完成。

从这个角度来看转动的自由度（不考虑质心的平动，因此选取的转轴总经过质心）：轴（取向）选取的自由度为 222，绕轴转动的自由度为 111。

平面运动 指存在一平面，使得刚体上任一点到该平面的垂直距离始终不变。此时转轴的取向不改变，转动自由度为 111，由于任意一点都被限制在一个平面上，对应的平动自由度为 222，总自由度为 333。

对于有限转动，若已知转轴 n^\hat{\bm{n}}n^，转动角度 ϕ\phiϕ，我们可以给出任意一点 r\bm{r}r 转动后对应的位置 r′\bm{r}'r′：

r′=(r⋅n^)n^+(r−(r⋅n^)n^)cos⁡ϕ+n^×rsin⁡ϕ(4)\bm{r}' = (\bm{r}\cdot\hat{\bm{n}})\hat{\bm{n}} + (\bm{r}-(\bm{r}\cdot\hat{\bm{n}})\hat{\bm{n}}) \cos\phi + \hat{\bm{n}}\times\bm{r}\sin\phi \tag{4} r′=(r⋅n^)n^+(r−(r⋅n^)n^)cosϕ+n^×rsinϕ(4)

考虑无限小转动，根据 (4)(4)(4) 得到：

r′=r+n^×rδϕ\bm{r'} = \bm{r} +\hat{\bm{n}}\times\bm{r} \delta\phi r′=r+n^×rδϕ

有：

δr=r−r′=n^×rδϕ(5)\delta \bm{r} = \bm{r} - \bm{r}' = \hat{\bm{n}}\times\bm{r} \delta\phi\tag{5} δr=r−r′=n^×rδϕ(5)

转动速度可写为：

v=ϕ˙n^×r=ω×r(6)\begin{aligned} \bm{v} &= \dot{\phi} \hat{\bm{n}} \times \bm{r}\\ & = \bm{\omega}\times\bm{r} \end{aligned}\tag{6} v​=ϕ˙​n^×r=ω×r​(6)

ω=ωn^\bm{\omega} = \omega \hat{\bm{n}}ω=ωn^ 为角速度矢量。

注意无穷小转动是可以交换的，因此对应的角速度是一个矢量，而角位移无法定义为一个矢量。

对于刚体上的任意点 PPP，其速度可以利用刚体角速度 ω\omegaω 与一给定点 AAA 速度 vAv_AvA​ 表出：

vP=vA+ω×(rP−rA)(7)\bm{v}_P = \bm{v}_A + \omega \times (\bm{r}_P - \bm{r}_A) \tag{7} vP​=vA​+ω×(rP​−rA​)(7)

利用式 (7)(7)(7) 可以给出刚体角动量的表达式。考虑刚体由 iii 个质量为 mim_imi​，位矢为 ri\bm{r}_iri​ 的质点构成。其角动量可以写为（以原点为参考点）：

L=∑imiri×[vA+ω×(ri−rA)]=MR×vA+M[(R⋅ω)rA−(R⋅rA)ω]+∑imi[ri2ω−(ri⋅ω)ri](8)\begin{aligned} \bm{L} &= \sum_i m_i\bm{r}_i \times [\bm{v}_A + \omega\times(\bm{r}_i - \bm{r}_A)]\\ &= M\bm{R}\times\bm{v}_A + M[(\bm{R}\cdot\bm{\omega})\bm{r}_A-(\bm{R}\cdot\bm{r}_A)\bm{\omega}] + \sum_i m_i[\bm{r}_i^2\bm{\omega}-(\bm{r}_i\cdot\bm{\omega})\bm{r}_i] \tag{8} \end{aligned} L​=i∑​mi​ri​×[vA​+ω×(ri​−rA​)]=MR×vA​+M[(R⋅ω)rA​−(R⋅rA​)ω]+i∑​mi​[ri2​ω−(ri​⋅ω)ri​]​(8)

我们来考虑表达式 (8)(8)(8) 各项的物理意义，第一项为所选取的参考点的平动所带来的角动量。若选取一固定点考察角动量，即 vA=0\bm{v}_A = 0vA​=0，那么第一项为零；第二项为质心的整体运动对应的角动量，若选取质心为参考点，即 rA=R\bm{r}_A = \bm{R}rA​=R，那么第二项恰好是刚体质心运动绕原点的角动量；第三项描述组成刚体的各个质点对应的角动量（扣除了整体平动部分），其与系统的质量分布密切相关。

其中第三项写出分量形式为：

Lμ=∑ν∑imi(ri2δμν−riμriν)ων=Iμνων=IμνωνL_{\mu} = \sum_{\nu}\sum_{i}m_i(r_i^2\delta_{\mu\nu}-r_{i\mu}r_{i\nu})\omega_{\nu} = I_{\mu\nu}\omega_{\nu} = I_{\mu\nu}\omega_{\nu} Lμ​=ν∑​i∑​mi​(ri2​δμν​−riμ​riν​)ων​=Iμν​ων​=Iμν​ων​

这里定义了惯量矩阵：

I=∑imi(ri2δμν−riμriν)(9)I = \sum_i m_i(r_i^2\delta_{\mu\nu}-r_{i\mu}r_{i\nu}) \tag{9} I=i∑​mi​(ri2​δμν​−riμ​riν​)(9)

于是有：

Lμ=Iμνων(10)L_{\mu} = I_{\mu\nu}\omega_{\nu} \tag{10} Lμ​=Iμν​ων​(10)

写为矩阵形式：

Iμν=∑imi(yi2+zi2−xiyi−xizi−xiyixi2+zi2−yizi−xizi−yizixi2+yi2)I_{\mu\nu} = \sum_i m_i\begin{pmatrix} y_i^2+z_i^2 & -x_iy_i & -x_iz_i \\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2+y_i^2 \\ \end{pmatrix} Iμν​=i∑​mi​⎝⎛​yi2​+zi2​−xi​yi​−xi​zi​​−xi​yi​xi2​+zi2​−yi​zi​​−xi​zi​−yi​zi​xi2​+yi2​​⎠⎞​

对于质量连续分布的系统，求和很自然的转变为积分。

分别选取原点、质心为参考点，利用 (8)(8)(8) 给出两种情况下的转动惯量：

I(A=O)=I(A=CM)+M[(R⋅R)ω−(R⋅ω)R]I(A=O)=I(A=CM) + M[(\bm{R}\cdot\bm{R})\bm{\omega} - (\bm{R}\cdot\bm{\omega})\bm{R}] I(A=O)=I(A=CM)+M[(R⋅R)ω−(R⋅ω)R]

此即 平行轴定理。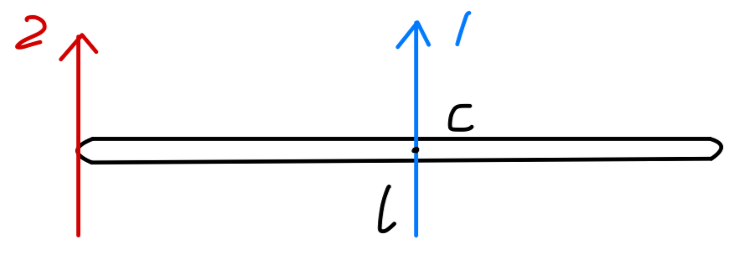

Fig1：匀质杆

绕轴 111:

I1=∫x2dm=∫−l2l2x2λdx=112λl3=112ml2\begin{aligned} I_1 &= \int x^2dm\\ &= \int_{-\frac{l}{2}}^{\frac{l}{2}} x^2\lambda dx\\ &= \frac{1}{12}\lambda l^3 = \frac{1}{12}ml^2\\ \end{aligned} I1​​=∫x2dm=∫−2l​2l​​x2λdx=121​λl3=121​ml2​

绕轴 222:

I2=∫x2dm=∫0lx2λdx=13λl3=13ml2\begin{aligned} I_2 &= \int x^2dm\\ &= \int_{0}^{l} x^2\lambda dx\\ &= \frac{1}{3}\lambda l^3 = \frac{1}{3}ml^2\\ \end{aligned} I2​​=∫x2dm=∫0l​x2λdx=31​λl3=31​ml2​

以上结果可以根据平行轴定理得到：

I2=I1+m(12l)2I_2 = I_1 + m(\frac{1}{2}l)^2 I2​=I1​+m(21​l)2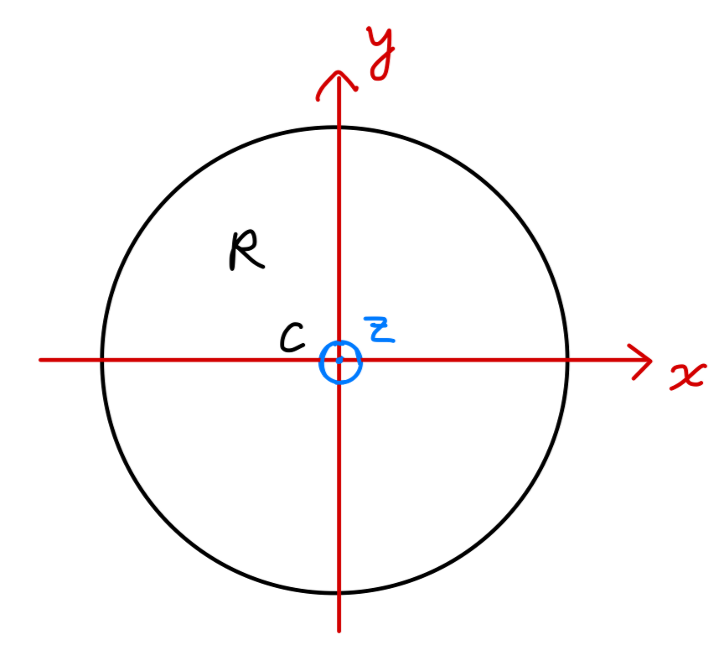

Fig2：圆盘

绕 zzz 轴：

Iz=∫ρ2dm=∬ρ2σρdρdθ=σ∫02πdθ∫0Rρ3dρ=π2σR4=12mR2\begin{aligned} I_{z} &= \int \rho^2 dm \\ &= \iint \rho^2 \sigma \rho d\rho d\theta\\ &= \sigma \int_{0}^{2\pi}d\theta \int_{0}^{R}\rho^3d\rho \\ &= \frac{\pi}{2}\sigma R^4 = \frac{1}{2}mR^2\\ \end{aligned} Iz​​=∫ρ2dm=∬ρ2σρdρdθ=σ∫02π​dθ∫0R​ρ3dρ=2π​σR4=21​mR2​

绕 xxx 轴（或绕 yyy 轴）：

Ix=∫ρ2dm=∬y2σdxdy=σ∫−RRdx∫−R2−x2R2−x2y2dy=σ∫−RR23(R2−x2)32dx=14mR2\begin{aligned} I_{x} &= \int \rho^2 dm \\ &= \iint y^2 \sigma dx dy\\ &= \sigma \int_{-R}^{R}dx \int_{-\sqrt{R^2-x^2}}^{\sqrt{R^2-x^2}}y^2dy \\ &= \sigma \int_{-R}^{R}\frac{2}{3}(R^2-x^2)^{\frac{3}{2}}dx\\ &= \frac{1}{4}mR^2\\ \end{aligned} Ix​​=∫ρ2dm=∬y2σdxdy=σ∫−RR​dx∫−R2−x2​R2−x2​​y2dy=σ∫−RR​32​(R2−x2)23​dx=41​mR2​

对于平面质量分布的系统，将有：

Iz=Ix+IyI_z = I_x + I_y Iz​=Ix​+Iy​

其中 zzz 轴为垂直于该平面的惯量主轴。

以上两种情形的惯性张量都是对角的，现在来看惯性张量非对角的情况。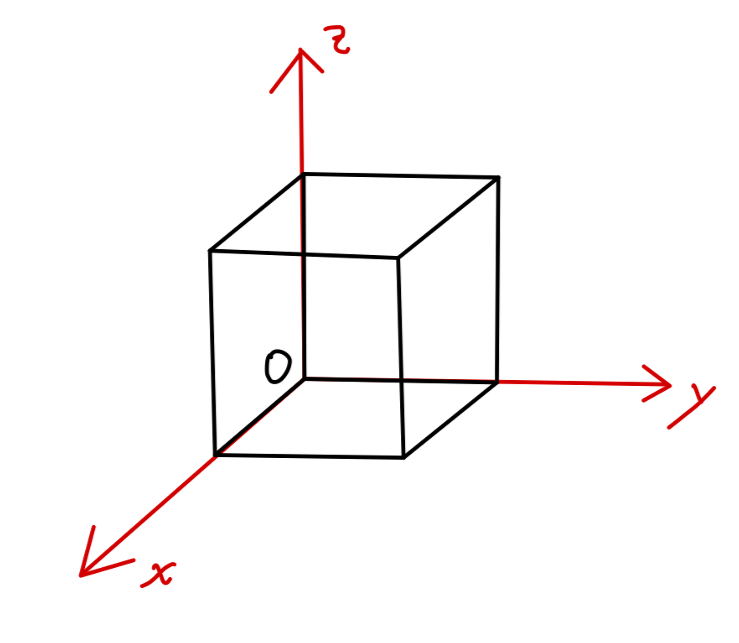

Fig3：立方体

计算绕着一个顶点的惯性张量：

I11=I22=I33=∭dxdydz(x2+y2)=23ma2I12=I13=I23=∭dxdydz(−xy)=−14ma2\begin{aligned} &I_{11} = I_{22} = I_{33} = \iiint dxdydz (x^2+y^2) = \frac{2}{3}ma^2\\ &I_{12} = I_{13} = I_{23} = \iiint dxdydz (-xy) = -\frac{1}{4}ma^2\\ \end{aligned} ​I11​=I22​=I33​=∭dxdydz(x2+y2)=32​ma2I12​=I13​=I23​=∭dxdydz(−xy)=−41​ma2​

于是其绕顶点的惯性张量矩阵为：

I=ma2(23−14−14−1423−14−14−1423)I = ma^2 \begin{pmatrix} \frac{2}{3} & -\frac{1}{4} & -\frac{1}{4}\\ -\frac{1}{4} & \frac{2}{3} & -\frac{1}{4}\\ -\frac{1}{4} & -\frac{1}{4} & \frac{2}{3}\\ \end{pmatrix} I=ma2⎝⎛​32​−41​−41​​−41​32​−41​​−41​−41​32​​⎠⎞​

一般来说，刚体的角动量 L\bm{L}L 与角速度 ω\bm{\omega}ω 并不同向。若角速度 ω\omegaω 沿着 III 的本征矢方向时，有：

Iωi=IiωiI\omega_i = I_i\omega_i Iωi​=Ii​ωi​

如此惯性张量的三个本征矢成为三个 惯量主轴，绕对应主轴的转动惯量为 主转动惯量。

例如将立方体绕顶点的转动惯量的本征值、本征矢量为：

I1=I2=1112ma2,I3=16ma2\begin{aligned} I_1 = I_2 = \frac{11}{12}ma^2,\quad I_3=\frac{1}{6}ma^2\\ \end{aligned} I1​=I2​=1211​ma2,I3​=61​ma2​

u1=(1−10)u2=(11−2)u3=(111)u_1 = \begin{pmatrix} 1\\ -1\\ 0\\ \end{pmatrix}\quad u_2 = \begin{pmatrix} 1\\ 1\\ -2\\ \end{pmatrix}\quad u_3 = \begin{pmatrix} 1\\ 1\\ 1\\ \end{pmatrix} u1​=⎝⎛​1−10​⎠⎞​u2​=⎝⎛​11−2​⎠⎞​u3​=⎝⎛​111​⎠⎞​

其中 u1,u2u_1,u_2u1​,u2​ 张成一个二维简并空间。惯性主轴可以取在这一平面中的任意方向。

刚体的动能写为：

T=∑i12mivi2=∑i12mivi⋅[vA+ω×(ri−rA)]=12MV⋅(vA−ω×rA)+12∑iω⋅(ri×mivi)=12MV⋅(vA−ω×rA)+12ω⋅L\begin{aligned} T &= \sum_{i}\frac{1}{2}m_i\bm{v}_i^2\\ &= \sum_{i}\frac{1}{2}m_i\bm{v}_i\cdot[\bm{v}_A + \bm{\omega}\times(\bm{r}_i - \bm{r}_A)]\\ &= \frac{1}{2}M\bm{V}\cdot(\bm{v}_A-\bm{\omega}\times\bm{r}_A) + \frac{1}{2}\sum_i\bm{\omega}\cdot(\bm{r}_i\times m_i\bm{v}_i)\\ &= \frac{1}{2}M\bm{V}\cdot(\bm{v}_A-\bm{\omega}\times\bm{r}_A) + \frac{1}{2}\bm{\omega}\cdot\bm{L}\\ \end{aligned} T​=i∑​21​mi​vi2​=i∑​21​mi​vi​⋅[vA​+ω×(ri​−rA​)]=21​MV⋅(vA​−ω×rA​)+21​i∑​ω⋅(ri​×mi​vi​)=21​MV⋅(vA​−ω×rA​)+21​ω⋅L​

其中第三项为刚体相对于质心的转动动能：

T=12Iμνωμων(11)T = \frac{1}{2}I_{\mu\nu}\omega_{\mu}\omega_{\nu} \tag{11} T=21​Iμν​ωμ​ων​(11)

考虑角速度沿着任意方向的情况，考虑沿着该方向作定轴转动的转动惯量为 InI_nIn​，那么转动的动能可以写为：

T=12Inω2=12Iijωiωj=12Iijcos⁡αicos⁡αjω2\begin{aligned} T &= \frac{1}{2}I_{n}\omega^2\\ &= \frac{1}{2}I_{ij}\omega_i\omega_j\\ &= \frac{1}{2}I_{ij}\cos\alpha_i\cos\alpha_j \omega^2 \\ \end{aligned} T​=21​In​ω2=21​Iij​ωi​ωj​=21​Iij​cosαi​cosαj​ω2​

如此得到：

In=Iijcos⁡αicos⁡αj(12)I_n = I_{ij}\cos\alpha_i\cos\alpha_j \tag{12} In​=Iij​cosαi​cosαj​(12)

令：xi=cos⁡αiInx_i = \frac{\cos\alpha_i}{\sqrt{I_n}}xi​=In​​cosαi​​，如此式 (12)(12)(12) 成为一个二次方程：

Iijxixj=1I_{ij}x_ix_j = 1 Iij​xi​xj​=1

这将对应一个椭球方程（因为惯性张量的三个本征值是正的，对应的动能是一个正定二次型），称为 惯量椭球。

惯量椭球具有如下性质：

∑ixi2=∑icos⁡2αi/In=1/In\sum_i x_i^2 = \sum_i \cos^2\alpha_i/I_n = 1/I_n i∑​xi2​=i∑​cos2αi​/In​=1/In​

∇if=2Iijxj=2Iijcos⁡αjIn=2IijωjωIn=2LiωIn\begin{aligned} \nabla_i f &= 2I_{ij}x_j\\ &= 2I_{ij}\frac{\cos\alpha_j}{\sqrt{I_n}}\\ &= \frac{2I_{ij}\omega_j}{\omega\sqrt{I_n}}\\ &= \frac{2L_i}{\omega\sqrt{I_n}}\\ \end{aligned} ∇i​f​=2Iij​xj​=2Iij​In​​cosαj​​=ωIn​​2Iij​ωj​​=ωIn​​2Li​​​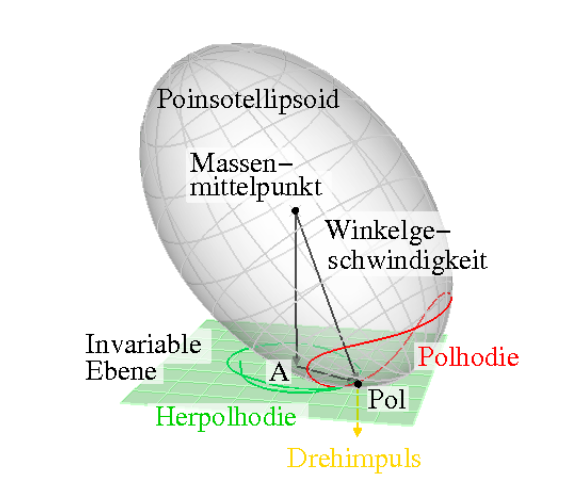

Fig4：潘索构造

潘索构造了一个利用几何方式可视化研究自由刚体运动的方法。称为 潘索构造。对于上图，我们注意到：

OA=OPω⋅LωL=2TIpωL=2TL\begin{aligned} OA &= OP \frac{\bm{\omega}\cdot\bm{L}}{\omega L}\\ &= \frac{2T}{\sqrt{I_p}\omega L}\\ &= \frac{\sqrt{2T}}{L}\\ \end{aligned} OA​=OPωLω⋅L​=Ip​​ωL2T​=L2T​​​

对于自由刚体来说，角动量与动能是守恒的。如此 OAOAOA 成为一个定值。因此刚体的运动可以等价为固定高度的惯量椭球在平面上的滚动，这将给出角速度的运动轨迹。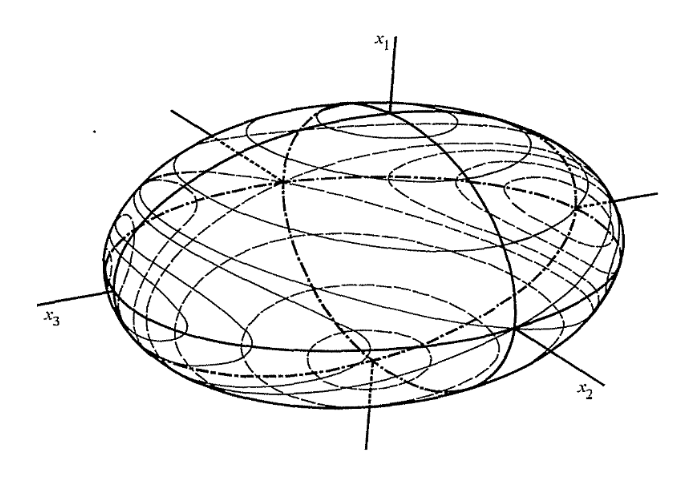

Fig5：比内椭球

给出能量与角动量为：

T=L122I1+L222I2+L322I3L2=L12+L22+L32(13)\begin{aligned} T &= \frac{L_1^2}{2I_1} + \frac{L_2^2}{2I_2} + \frac{L_3^2}{2I_3}\\ L^2 &= L_1^2 + L_2^2 + L_3^2\\ \end{aligned}\tag{13} TL2​=2I1​L12​​+2I2​L22​​+2I3​L32​​=L12​+L22​+L32​​(13)

自由刚体在运动中角动量与能量守恒，式 (13)(13)(13) 给出的椭圆与球的交线将给出角动量在本体坐标系中的运动轨迹。

通过潘索构造与比内椭球我们可以发现：只有绕着最小和最大的主转动惯量的主轴方向的转动才是稳定的。