有效质量和电导有效质量以及状态密度有效质量之间有什么关系？能够分别解释以及互相对比一下吗？

您所在的位置：网站首页 › 状态密度表达式 › 有效质量和电导有效质量以及状态密度有效质量之间有什么关系？能够分别解释以及互相对比一下吗？

有效质量和电导有效质量以及状态密度有效质量之间有什么关系？能够分别解释以及互相对比一下吗？

2024-03-15 02:02| 来源: 网络整理| 查看: 265

引入有效质量这个概念能够使半导体中的各种计算模型大大简化~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~电导有效质量和态密度有效质量的关系：同出一源，但又花开两朵各表一枝。

相同点：数学上来说，两者都来源于晶体EK关系（或者叫色散关系、能带）的二阶泰勒展开项系数矩阵，由该系数矩阵可导出张量形式的有效质量（注意：张量形式的有效质量并未区分电导有效质量和态密度有效质量）。在各向同性的情况下，两种有效质量等价。

不同点：在各项异性的情况下，为了简化问题，需要对各个方向有效质量进行平均，两种有效质量的平均方法不同。电导有效质量，采用调和平均： $\frac{1}{m^{*}} =\frac{1}{3}(\frac{1}{m_{x}^{*}}+\frac{1}{m_{y}^{*}}+\frac{1}{m_{z}^{*}} )$ 态密度有效质量，采用几何平均： $m^{*}=\sqrt[3]{m_{x}^{*}m_{y}^{*}m_{z}^{*}}$ 从用途上看，顾名思义，电导有效质量描述的是材料的导电性能，是在经典模型下（把电子当做实物粒子）的物理量，最常用的地方就是计算载流子迁移率。态密度有效质量，通常用来研究材料中有关电子统计的各种问题，如跃迁过程（光子吸收、光子辐射、以及各种散射过程）、金属电子的热容量、半导体电子的热激发等等。~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~下面详细展开：想要了解两者的渊源，得从EK关系开始谈起

1.EK关系—描述晶体中电子特性的基本框架

在量子力学的视角下，我们不再以实物粒子的身份看待晶体中的电子，而是用波函数来描述。求解周期性势场中的薛定谔方程，可以得到电子在晶体中一组完备的本征态和能量本征值，完备的含义是电子的任意一个状态都可以由这样一组本征解展开，接着我们可以建立能量本征值E和波函数波矢K的关系，即所谓的EK关系。至此，有了EK关系和对应的波函数，描述晶体中电子特性的基本框架就已经搭好了。各位看官且看如何玩转这EK关系，架起从微观到宏观的桥梁，从而得到材料的电学性能以及光学性能（一不小心暴露了出身）。

为了给大家留点印象，先来看看啥是EK关系。体材料中，由于k空间是三维空间，直观起见，我们通常只画出高对称点连线的EK关系，下图分别是体材料Si和Ge的EK关系：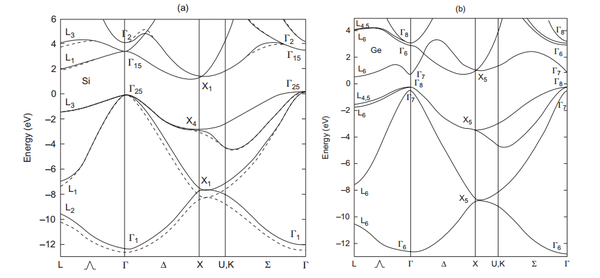

但应当意识到，EK关系是三维空间的函数E（kx，ky，kz）还有一种用等能面表示三维EK关系的方法：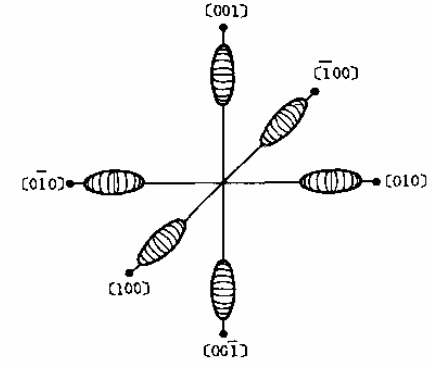

由于EK曲面在各个方向上弯曲程度（有效质量）不一样，所以等能面是椭球面。

2.波包—量子力学与经典力学的桥梁

材料的导电性能，是在经典力学范畴的概念，这个时候需要将电子看做实物粒子，引入质量、速度等物理量。然而，描述电子状态是在量子力学的框架内完成的，所以问题就变成了如何将电子的波函数形式描述转移到经典力学中来。这个时候，需要引入波包的模型。所谓波包，是一系列本征态的叠加，波包的运动在一定的限度内可以与经典粒子的运动相对应。在晶体中，与量子态K0对应的波包是把K0与k0附近k'范围内的状态叠加所得。经过推导（以下引自黄昆《固体物理》），波包函数的模方为：

$\left| \psi \left( r,t \right) \right| ^{2}=\left| u_{k0}(r) \right|^{2}\left| \frac{sin(\Delta u/2)}{\Delta u/2} \right| ^{2} \left| \frac{sin(\Delta v/2)}{\Delta v/2} \right| ^{2} \left| \frac{sin(\Delta w/2)}{\Delta w/2} \right| ^{2} \Delta ^{6}$

其中，u,v,w为：

$u=x-\frac{1}{hbar} (\frac{\partial E}{\partial k_{x}} )_{k_{0}}\cdot t$ $v=y-\frac{1}{hbar} (\frac{\partial E}{\partial k_{y}} )_{k_{0}}\cdot t$ $w=z-\frac{1}{hbar} (\frac{\partial E}{\partial k_{z}} )_{k_{0}}\cdot t$

波包具有如下图所示的形状：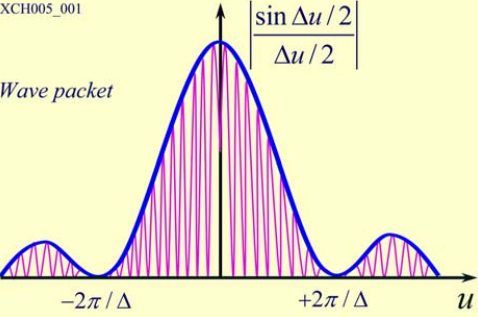

上面的表达式中的u，v，w说明波包中心位置随着时间变化在移动，如果将波包看做一个准粒子，则其速度为：

$v_{k0} =\frac{1}{hbar} (\frac{\partial E}{\partial kx} e_{x}+\frac{\partial E}{\partial ky}e_{y}+\frac{\partial E}{\partial kz}e_{z})_{k0}$

其中， $e_{x},e_{y},e_{z}$ 分别为x，y，z方向上的单位矢量。

为了引入质量，对速度做时间微分，得到加速度：

$\frac{dv_{k0}}{dt} =\frac{d}{dt} (\frac{1}{hbar} (\frac{\partial E}{\partial kx}e_{x} +\frac{\partial E}{\partial ky}e_{y}+\frac{\partial E}{\partial kz}e_{z})_{k0})$

利用链式法则：

$\frac{dv_{k0}}{dt} =\frac{1}{hbar}\sum_{a}^{}{\frac{dk_{a}}{dt} } \frac{\partial }{\partial k_{a}} (\frac{\partial E}{\partial kx} e_{x}+\frac{\partial E}{\partial ky}e_{y}+\frac{\partial E}{\partial kz}e_{z})_{k0}$

然后，将加速度写成矩阵形式：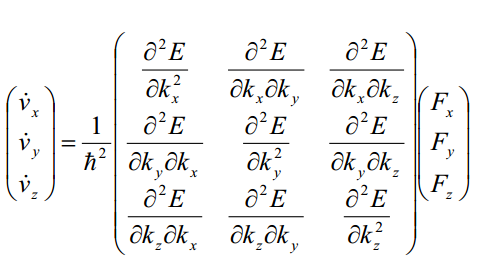

与牛顿定律对比：

$\frac{dv}{dt} =\frac{1}{m}F$

不难发现F的系数矩阵就是倒过来的质量，经过主轴变换总可以找到一组基使得非对角元为零,此时的有效质量张量形式简洁：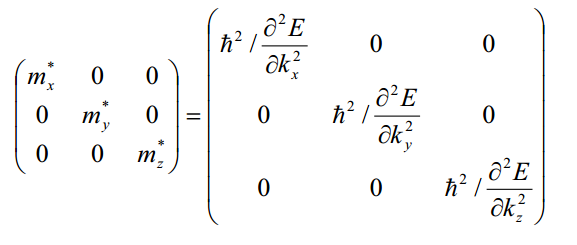

这里出现了三个独立分量mx，my，mz，如果这三者不相等，则表示存在各向异性。至此，我们有了有效质量的概念，从几何上来看有效质量与曲面的弯曲程度直接相关，曲面越弯曲则有效质量越小，相反越平坦则有效质量越大。接下来看什么是电导有效质量。

3.电导有效质量

电导率是描述导电性能的一个重要参数，其定义为：

$\sigma =ne\mu$

其中 $\mu$ 为电子迁移率，表征单位电场下载流子的迁移速度：

$\mu =e\tau /m^{*}$

$m^{*}$ 即为电导有效质量，如果EK关系是各向同性，非常好办，电导有效质量张量直接退化成标量。

如果EK关系各项异性，即mx，my，mz三者不相等。那么有效质量为张量。但是张量形式的方程对于实际应用太过复杂。比如欧姆定律就要写成：

$J_{x}=ne^{2}\tau \frac{1}{3}(\frac{1}{m_{xx}} +\frac{1}{m_{xy}} +\frac{1}{m_{xz}} ) E_{x}$ $J_{y}=ne^{2}\tau \frac{1}{3}(\frac{1}{m_{yx}} +\frac{1}{m_{yy}} +\frac{1}{m_{yz}} ) E_{y}$ $J_{z}=ne^{2}\tau \frac{1}{3}(\frac{1}{m_{zx}} +\frac{1}{m_{zy}} +\frac{1}{m_{zz}} ) E_{z}$

为了避免使用张量方程，人们想了一个偷懒的办法，对有效质量做平均，注意到m位置是在分母上，所以平均的形式应当为（调和平均）：

$\frac{1}{m^{*}} =\frac{1}{3}(\frac{1}{m_{x}^{*}}+\frac{1}{m_{y}^{*}}+\frac{1}{m_{z}^{*}} )$

至此，我们已经清楚了电导有效质量的含义。

4.态密度有效质量

在研究半导体中电子的特性时，我们用统计物理中的费米-狄拉克分布来描述电子的分布状态，那么就会引入有关费米-狄拉克函数的积分。为了数学计算的方便，我们常常对半导体的EK关系采用抛物带近似（自由电子近似），将EK关系展开到二阶项，这里的mx，my，mz与电导有效质量中的mx，my，mz一致：

$E(k)=E_{0}+\frac{hbar^{2}}{2} (\frac{k_{x}^{2}}{m_{x}^{*}}+\frac{k_{y}^{2}}{m_{y}^{*}}+\frac{k_{z}^{2}}{m_{z}^{*}} )$

该式的物理含义是将周期性势场对电子的散射作用归结到电子质量的改变上。

若mx，my，mz不相等，意味着存在各项异性。为了进一步简化计算，我们同样需要对mx，my，mz做平均。但其平均的方法与电导有效质量有所不同，原因稍后解释:

$m^{*}=\sqrt[3]{m_{x}^{*}m_{y}^{*}m_{z}^{*}}$

通过有效质量的平均，EK关系近似为：

$E(k)=E_{0}+\frac{hbar^{2}}{2m^{*}} (k_{x}^{2}+k_{y}^{2}+k_{z}^{2})$

这里的 $m^{*}$ 即态密度有效质量

5.为何叫态密度有效质量？

我们知道，半导体中的能带实际上是由无数个分立的准连续状态所组成。如下图所示：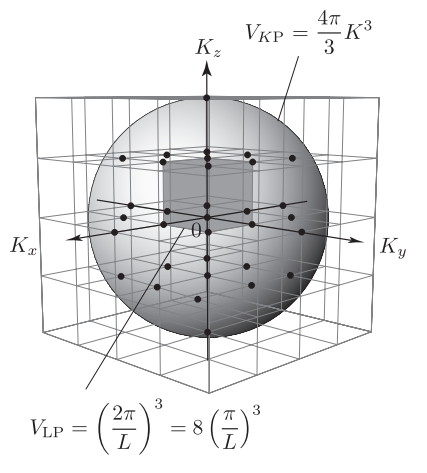

然而，我们进行理论分析的时候通常是把K空间当成连续地来处理，因为这样可以将求和运算转变为积分运算。态密度的作用就是将离散的求和与连续的积分联系起来。

如计算载流子浓度的公式：

$N=\frac{1}{8\pi ^{3}} \int_{}^{} d^{3}k f(E_{k})$

其中 $f(E_{k})=\frac{1}{1+exp((E_{k}-E_{F})/K_{b}T)}$ ，为费米狄拉克分布函数

注意到，这里积分域是三维的k空间，将离散的k空间近似为连续的k空间，所以需要乘以一个离散K空间到连续K空间的态密度系数。然而，人们觉得三重积分算起来太麻烦，于是对它做进一步处理，从K空间变换到E空间，最终将一个三维各项异性的K空间转变为一维的E空间，大大简化了计算。

$N= \int_{}^{} dE f(E)g(E)$

由于这种方法在抛物带近似成立的情况下其误差尚可接受，且计算方法较为简单，所以被广泛采用。其中g（E）即为E空间的态密度，其含义是单位能量间隔的状态数。

对于体材料，g（E）的表达式为：

$g(E)=4\pi (\frac{2m^{*}}{h^2} ) ^{\frac{3}{2} }\sqrt{E}$

至此，可以看出态密度有效质量的物理含义。态密度有效质量越大，单位能量间隔电子的状态数越多，反之状态数越少。

接下来，简单讨论下为什么态密度有效质量的平均方式是这样的：

$m^{*}=\sqrt[3]{m_{x}^{*}m_{y}^{*}m_{z}^{*}}$

我们知道，dE与dK的关系为：

$g(E)dE=dk_{x}dk_{y}dk_{z}$

两边做立方

$g(E)^{3}d^{3}E=d^{3}k_{x}d^{3}k_{y}d^{3}k_{z}=g_{x}(E)g_{y}(E)g_{z}(E)d^{3}E$

得到

$g(E)=\sqrt[3]{g_{x}(E)g_{y}(E)g_{z}(E)}$ 将g(E)表达式代入，不难发现具有几何平均的形式： $m^{*}=\sqrt[3]{m_{x}^{*}m_{y}^{*}m_{z}^{*}}$ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~以上是我个人理解，难免有失偏颇，欢迎大家批评指正

修改说明（2020年1月24日）：波包的群速度 $v_{k0}$ 应为矢量，上一版本中遗漏了 $e_{x},e_{y},e_{z}$ 方向矢量，已改正。感谢 @费米能级指出。~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~有兴趣可参考：[1] 电子的准经典运动、波包：黄昆《固体物理》[2] 电导有效质量和态密度有质量的平均方法：《LASER DIODES AND THEIR APPLICATIONS TO COMMUNICATIONS ANDINFORMATION PROCESSING》 P381~384wikipedia：Effective mass (solid-state physics)

【本文地址】

有效质量和电导有效质量以及状态密度有效质量之间有什么关系？能够分别解释以及互相对比一下吗？

有效质量和电导有效质量以及状态密度有效质量之间有什么关系？能够分别解释以及互相对比一下吗？

今日新闻

推荐新闻