【最优化笔记2】线性规划 |
您所在的位置:网站首页 › 求解线性规划问题的有效方法有哪些 › 【最优化笔记2】线性规划 |
【最优化笔记2】线性规划
|
线性规划(LP)就是由目标函数为决策变量的线性函数和约束条件为线性等式或线性不等式所组成的数学规划。 文章目录 1.线性规划的标准形式2.求解前的理论准备2.1 基本可行解(1)定义(2)性质 2.2 线性规划基本定理(1)先行理论(2)线性规划基本定理 1.线性规划的标准形式这里直接给出线性规划的矩阵标准形式,这是接下来讨论的基础。 { m i n c T x s . t . A x = b , x ≥ 0 (1) \begin{cases}min c^Tx \\ s.t. Ax=b,& \text{$x\geq0 $ } \end{cases} \tag{1} {mincTxs.t.Ax=b,x≥0 (1) 其中 x = ( x 1 , x 2 , . . . , x n ) T x=(x_1,x_2,...,x_n)^T x=(x1,x2,...,xn)T,为决策变量 A = ( a i j ) m × n , r a n k ( A ) = m ≤ n A=(a_{ij})_{m \times n}, rank(A)=m \leq n A=(aij)m×n,rank(A)=m≤n,为约束方程系数。 c = ( c 1 , c 2 , . . . , c n ) T c=(c_1,c_2,...,c_n)^T c=(c1,c2,...,cn)T,为目标函数系数。 b = ( b 1 , b 2 , . . . , b m ) 并 且 b i ≥ 0 , i = 1 , 2 , . . . , m b=(b_1,b_2,...,b_m) 并且b_i\geq0,i=1,2,...,m b=(b1,b2,...,bm)并且bi≥0,i=1,2,...,m,为约束条件右端常数。 通过 1.引入松弛变量和剩余变量,将线性不等式化约束为等式约束约束。 2.设 x p x_p xp为自由变量,即 x p ∈ R x_p \in R xp∈R,令 x p = u 1 − u 2 , u 1 , u 2 ≥ 0 x_p=u_1-u_2,u_1,u_2 \geq 0 xp=u1−u2,u1,u2≥0,或者通过约束等式将 x p x_p xp替换掉将自由变量处理为符号条件( ≥ 0 \geq0 ≥0)的变量即可。 将线性规划非标准型化为标准型将是求解的第一步。 2.求解前的理论准备为了进行下一步的求解,我们这里首先介绍几个重要的概念和定律。 从A的n列中选出m列,使它们相信无关,不妨设A的前m列线性无关,即
a
j
=
(
a
1
j
,
a
2
j
,
.
.
.
,
a
n
j
)
,
j
=
1
,
2
,
.
.
.
m
a_j=(a_{1j},a_{2j},...,a_{nj}),j=1,2,...m
aj=(a1j,a2j,...,anj),j=1,2,...m是线性无关的。令 显然,一个m阶n维的线性规划问题,其基本可行解个数不超过 C n m C_n^m Cnm,这保证了线性规划的基本可行解个数是有限的。 2.2 线性规划基本定理 (1)先行理论1.闭半空间:称 H + = H^+= H+={ x ∣ x ∈ R n , c T x ≥ b x|x\in R^n,c^Tx\geq b x∣x∈Rn,cTx≥b}为正闭半空间, H − = H^-= H−={ x ∣ x ∈ R n , c T x ≤ b x|x\in R^n,c^Tx\leq b x∣x∈Rn,cTx≤b}为负闭半空间, H + H^+ H+和 H − H^- H−统称为闭半空间。 易证闭半空间为凸集。 2.多面凸集 S S S:有限个闭半空间的交集称为多面凸集,亦即集合 S S S={ x ∣ A x ≤ b x| Ax\leq b x∣Ax≤b},(其中 A = ( a i j ) m × n A=(a_{ij})_{m \times n} A=(aij)m×n)。 由凸集的性质(有限个凸集的交集仍为凸集)知S为凸集。 下面的内容很重要 |
【本文地址】
今日新闻 |
推荐新闻 |

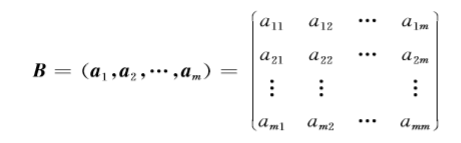 显然B是满秩的,因此方程组
B
x
=
b
Bx=b
Bx=b 有唯一的解
x
B
=
B
−
1
b
,
x_B=B^{-1}b,
xB=B−1b,令
x
=
(
x
B
T
,
0
T
)
x=(x_B^T,0^T)
x=(xBT,0T),x即前m个分量等于
x
B
,
x_B,
xB,后n-m个分量赋为0,则得到约束方程组的一个解。 称B为基\基底,称这样得到的解矢量
x
x
x为约束方程组关于基底B的基本解。而与B相对应的
x
x
x的分量
x
i
x_i
xi成为基本变量。当基本解中有一个或一个以上的基本变量
x
i
x_i
xi为0时,则称这个解为退化的基本解。当一个可行解
x
x
x又是基本解时(满足约束条件同时分量
x
i
x_i
xi都是非负值),则称它是基本可行解。若它是退化的,则称它是退化的基本可行解。
显然B是满秩的,因此方程组
B
x
=
b
Bx=b
Bx=b 有唯一的解
x
B
=
B
−
1
b
,
x_B=B^{-1}b,
xB=B−1b,令
x
=
(
x
B
T
,
0
T
)
x=(x_B^T,0^T)
x=(xBT,0T),x即前m个分量等于
x
B
,
x_B,
xB,后n-m个分量赋为0,则得到约束方程组的一个解。 称B为基\基底,称这样得到的解矢量
x
x
x为约束方程组关于基底B的基本解。而与B相对应的
x
x
x的分量
x
i
x_i
xi成为基本变量。当基本解中有一个或一个以上的基本变量
x
i
x_i
xi为0时,则称这个解为退化的基本解。当一个可行解
x
x
x又是基本解时(满足约束条件同时分量
x
i
x_i
xi都是非负值),则称它是基本可行解。若它是退化的,则称它是退化的基本可行解。 3.凸集S的顶点(极点):
x
∈
S
,
x\in S,
x∈S,若找不到
x
1
,
x
2
∈
S
(
x
1
≠
x
2
)
,
x_1,x_2\in S(x_1\not=x_2),
x1,x2∈S(x1=x2),使得
x
=
a
x
1
+
(
1
−
a
)
x
2
(
0
<
a
<
1
)
x=ax_1+(1-a)x_2(0
3.凸集S的顶点(极点):
x
∈
S
,
x\in S,
x∈S,若找不到
x
1
,
x
2
∈
S
(
x
1
≠
x
2
)
,
x_1,x_2\in S(x_1\not=x_2),
x1,x2∈S(x1=x2),使得
x
=
a
x
1
+
(
1
−
a
)
x
2
(
0
<
a
<
1
)
x=ax_1+(1-a)x_2(0