矩阵求导常用公式(避坑)+矩阵的模和矩阵的绝对值的求导 |
您所在的位置:网站首页 › 求矩阵的绝对值公式 › 矩阵求导常用公式(避坑)+矩阵的模和矩阵的绝对值的求导 |
矩阵求导常用公式(避坑)+矩阵的模和矩阵的绝对值的求导
|
目录
矩阵求导常用公式1.分母布局与分子布局2.分母布局与分子布局的矩阵求导公式(1)向量对向量求导(2)、标量对向量求导(3)、向量对标量求导3.验证求导结果矩阵的模和矩阵的绝对值的求导1,矩阵的绝对值求导(1)f是一个标量(2)f是一个矢量2,矩阵的模求导
矩阵求导常用公式
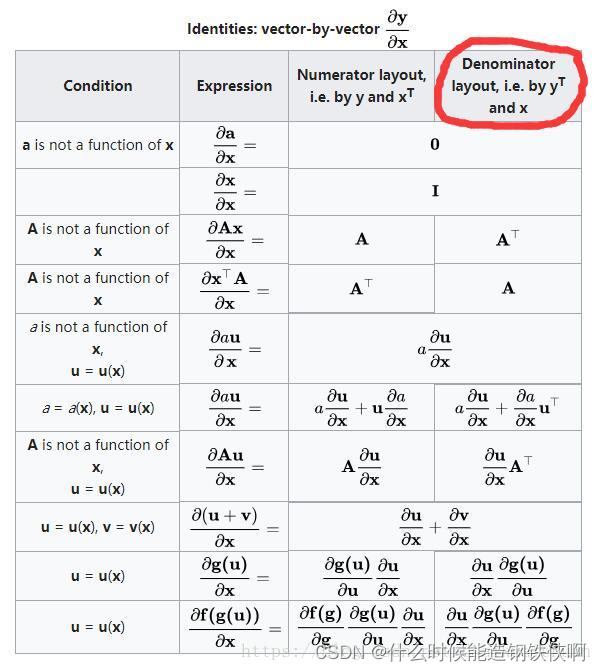
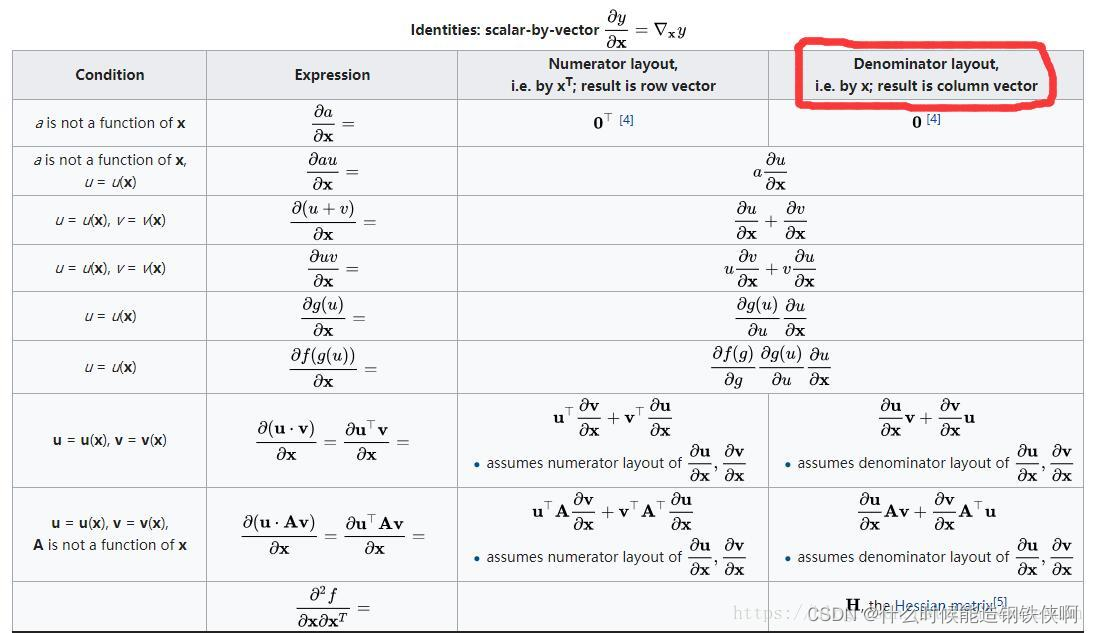
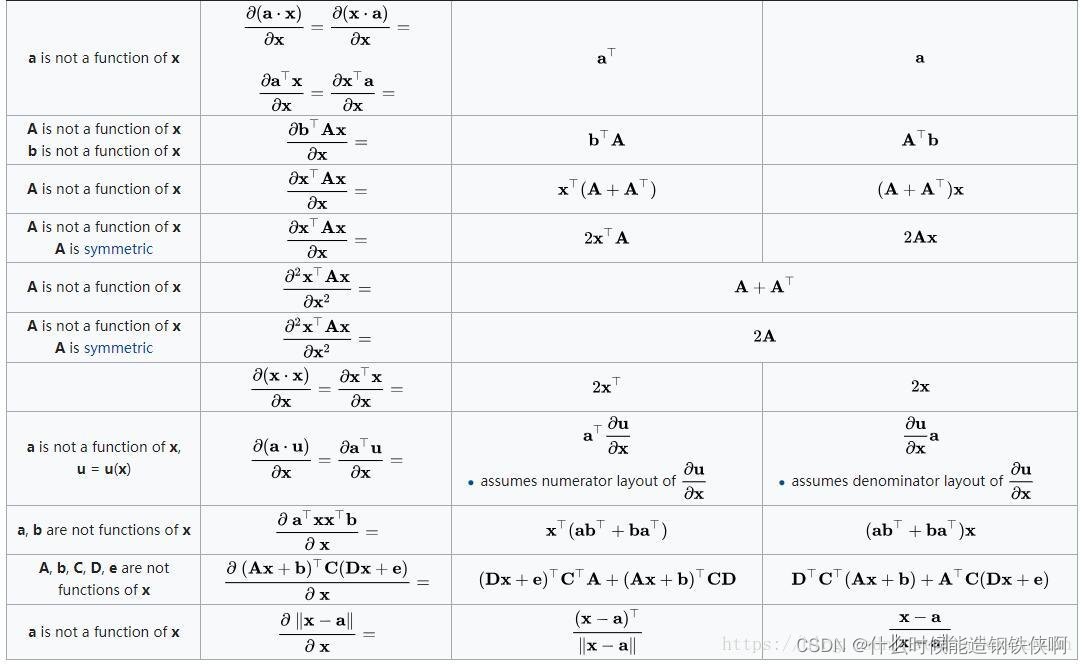
1.分母布局与分子布局
(1) 前提: 1.分子分母都是向量,且一个是行向量,另一个是列向量 2.分子分母一个是标量,另一个是行向量或列向量 当满足1或2时,讨论分母布局/分子布局才有意义。 (2). 结论:谁是列向量就是什么布局。 分母是列向量,就是分母布局;分子是列向量,就是分子布局。 (3). 一个例子:定义一般的列向量 x = ( x 1 , x 2 , ⋯ , x n ) T x=(x_1,x_2,\cdots,x_n)^\mathrm{T} x=(x1,x2,⋯,xn)T 的矩阵函数 a ( x ) = [ a 1 ( x ) , a 2 ( x ) , ⋯ , a s ( x ) ] T a(x)=[a_1(x),a_2(x),\cdots ,a_s(x)]^\mathrm{T} a(x)=[a1(x),a2(x),⋯,as(x)]T a a a对 x T x^\mathrm{T} xT的导数为 d a d x T = [ ∂ a 1 ∂ x 1 ∂ a 1 ∂ x 2 ⋯ ∂ a 1 ∂ x n ⋯ ⋯ ⋯ ⋯ ∂ a s ∂ x 1 ∂ a s ∂ x 2 ⋯ ∂ a s ∂ x n ] \dfrac{da}{dx^\mathrm{T}}=\begin{bmatrix} \dfrac{\partial a_1}{\partial x_1}&\dfrac{\partial a_1}{\partial x_2}&\cdots&\dfrac{\partial a_1}{\partial x_n}\\ \cdots&\cdots&\cdots&\cdots\\ \dfrac{\partial a_s}{\partial x_1}&\dfrac{\partial a_s}{\partial x_2}&\cdots&\dfrac{\partial a_s}{\partial x_n}\\ \end{bmatrix} dxTda=⎣⎢⎢⎢⎡∂x1∂a1⋯∂x1∂as∂x2∂a1⋯∂x2∂as⋯⋯⋯∂xn∂a1⋯∂xn∂as⎦⎥⎥⎥⎤ 可以看到,此时为分子布局,因为 a a a 是 s × 1 s \times 1 s×1 的列向量, x T x^\mathrm{T} xT是 1 × n 1 \times n 1×n 的行向量,所以结果是 s × n s \times n s×n 的。 而 a T a^\mathrm{T} aT对 x x x 的导数为 d a T d x = [ ∂ a 1 ∂ x 1 ∂ a 2 ∂ x 1 ⋯ ∂ a s ∂ x 1 ⋯ ⋯ ⋯ ⋯ ∂ a 1 ∂ x n ∂ a 2 ∂ x n ⋯ ∂ a s ∂ x n ] \dfrac{da^\mathrm{T}}{dx}=\begin{bmatrix} \dfrac{\partial a_1}{\partial x_1}&\dfrac{\partial a_2}{\partial x_1}&\cdots&\dfrac{\partial a_s}{\partial x_1}\\ \cdots&\cdots&\cdots&\cdots\\ \dfrac{\partial a_1}{\partial x_n}&\dfrac{\partial a_2}{\partial x_n}&\cdots&\dfrac{\partial a_s}{\partial x_n}\\ \end{bmatrix} dxdaT=⎣⎢⎢⎢⎡∂x1∂a1⋯∂xn∂a1∂x1∂a2⋯∂xn∂a2⋯⋯⋯∂x1∂as⋯∂xn∂as⎦⎥⎥⎥⎤ 可以看到,此时为分母布局,因为 x x x是 n × 1 n \times 1 n×1 的列向量, a T a^\mathrm{T} aT 是 1 × s 1 \times s 1×s的行向量,所以结果是 n × s n \times s n×s 的。 (4). 总结:直接去看别人的矩阵公式你得先知道自己的矩阵布局不然都搞错了 2.分母布局与分子布局的矩阵求导公式Denominator layout 是分母布局,Numerator layout是分子布局 常用的是分母布局,图中标红。 (1)向量对向量求导
在这里同时给出一个自动求导的网站链接:链接: link 可以验证你的求导结果。 矩阵的模和矩阵的绝对值的求导最近推导一些公式,对矩阵求导遇到一些问题,在这里纪录一下 1,矩阵的绝对值求导 (1)f是一个标量假设函数 f = f ( x ) f=f(x) f=f(x),对 ∣ f ∣ |f| ∣f∣求导: 结论: ∣ f ∣ ′ = f ∣ f ∣ ⋅ f ′ |f|'=\dfrac{f}{|f|} \cdot f' ∣f∣′=∣f∣f⋅f′ 推导: 向两边平方 ∣ f ∣ 2 = f 2 |f|^2=f^2 ∣f∣2=f2 再两边求导 2 ∣ f ∣ ′ ∣ f ∣ = 2 f ′ f 2|f|'|f|=2f'f 2∣f∣′∣f∣=2f′f ⇒ \Rightarrow ⇒ ∣ f ∣ ′ = f ∣ f ∣ ⋅ f ′ |f|'=\dfrac{f}{|f|} \cdot f' ∣f∣′=∣f∣f⋅f′ (2)f是一个矢量当f是一个矢量仍然有类似的结果 结论: ∣ f ⃗ ∣ ′ = f ⃗ ∣ f ⃗ ∣ ⋅ f ⃗ ′ |\vec f|'=\dfrac{\vec f}{|\vec f|} \cdot \vec f' ∣f ∣′=∣f ∣f ⋅f ′ 推导: 向两边平方 ∣ f ⃗ ∣ 2 = f ⃗ 2 |\vec f|^2=\vec f^2 ∣f ∣2=f 2 再两边求导 2 ∣ f ⃗ ∣ ′ ∣ f ⃗ ∣ = 2 f ⃗ ′ f ⃗ 2|\vec f|'|\vec f|=2\vec f'\vec f 2∣f ∣′∣f ∣=2f ′f ⇒ \Rightarrow ⇒ ∣ f ⃗ ∣ ′ = f ⃗ ∣ f ⃗ ∣ ⋅ f ⃗ ′ |\vec f|'=\dfrac{\vec f}{|\vec f|} \cdot \vec f' ∣f ∣′=∣f ∣f ⋅f ′ 2,矩阵的模求导注意这里是模的导数,不是模的平方的导数!!! 这里是分母布局 ∥ A X ∥ = ( A X ) T ( A X ) = ( X T A T A X ) 1 2 \|AX\|=\sqrt{(AX)^\mathrm{T}(AX)}=(X^\mathrm{T}A^\mathrm{T}AX)^\frac{1}{2} ∥AX∥=(AX)T(AX) =(XTATAX)21 求导 ⇒ \Rightarrow ⇒ 1 2 ( X T A T A X ) − 1 2 ( 2 A T A X ) \dfrac{1}{2}(X^\mathrm{T}A^\mathrm{T}AX)^{-\frac{1}{2}}(2A^\mathrm{T}AX) 21(XTATAX)−21(2ATAX) ⇒ A T A X ∥ A X ∥ \Rightarrow \dfrac{A^\mathrm{T}AX}{\|AX\|} ⇒∥AX∥ATAX 参考: https://blog.csdn.net/daaikuaichuan/article/details/80620518 https://zhuanlan.zhihu.com/p/491935204 https://www.zhihu.com/question/352174717 https://en.wikipedia.org/wiki/Matrix_calculus |
【本文地址】
今日新闻 |
推荐新闻 |