概率论之 |
您所在的位置:网站首页 › 正态分布的方差等于负数吗 › 概率论之 |
概率论之
|
概率论之——高斯分布的乘积
一、前言二、高斯分布(正态分布)标准高斯分布高斯分布的基本性质
三、高斯分布的乘积python示意图
四、多维高斯分布五、共轭分布后记
一、前言
本来我并不想开机器学习这个专栏,因为机器学习与高数线代矩阵论概率论密切相关,我的数学能力没达到这种高度。然而控制理论也会涉及各种数理统计知识,那就不得不开一个数理栏了。 这个栏没有具体的知识路线,写到哪算哪,数学和机器学习相关且不好分类的东西都会往这边放。 二、高斯分布(正态分布)假设随机变量 x 1 x_1 x1服从均值和方差为 μ 1 , σ 1 2 \mu_1, \ \sigma_1^2 μ1, σ12的高斯分布,可记作 x 1 ∼ N ( μ 1 , σ 1 ) x_1 \sim N(\mu_1, \ \sigma_1) x1∼N(μ1, σ1),其概率密度函数为: p ( x 1 ) = 1 2 π σ 1 exp [ − ( x − μ 1 ) 2 2 σ 1 2 ] p(x_1)= \frac {1} {\sqrt {2\pi}\sigma_1} \exp [ - \frac {(x-\mu_1)^2}{2\sigma_1^2}] p(x1)=2π σ11exp[−2σ12(x−μ1)2] 标准高斯分布如果随机变量 x ∼ N ( 0 , 1 ) x \sim N(0, 1) x∼N(0,1),则称 x x x服从标准高斯(正态)分布: p ( x ) = 1 2 π exp ( − x 2 2 ) p(x)=\frac {1}{\sqrt {2\pi}} \exp ( - \frac {x^2}{2}) p(x)=2π 1exp(−2x2) 高斯分布的基本性质假设 x ∼ N ( μ , σ 2 ) x\sim N(\mu, \sigma^2) x∼N(μ,σ2),有: a x + b ∼ N ( a μ + b , a 2 μ 2 ) , a , b ∈ R ax+b \sim N(a\mu+b,a^2\mu^2)\ ,a,b\in R ax+b∼N(aμ+b,a2μ2) ,a,b∈R 假设 x ∼ N ( μ x , σ x 2 ) x\sim N(\mu_x, \sigma_x^2) x∼N(μx,σx2), y ∼ N ( μ y , σ y 2 ) y\sim N(\mu_y, \sigma_y^2) y∼N(μy,σy2), x , y x,y x,y是独立随机变量,有: x + y ∼ N ( μ x + μ y , σ x 2 + σ y 2 ) x+y\sim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2) x+y∼N(μx+μy,σx2+σy2) 三、高斯分布的乘积进入正题。假设两个独立随机变量 x ∼ N ( μ x , σ x 2 ) x\sim N(\mu_x, \sigma_x^2) x∼N(μx,σx2), y ∼ N ( μ y , σ y 2 ) y\sim N(\mu_y, \sigma_y^2) y∼N(μy,σy2),则它们的乘积符合高斯概率密度函数的形式: ( x , y ) ∼ N ( μ y σ x 2 + μ x σ y 2 σ x 2 + σ y 2 , 1 1 / σ x 2 + 1 / σ y 2 ) (x,y)\sim N(\frac {\mu_y\sigma_x^2+\mu_x\sigma_y^2} {\sigma_x^2+\sigma_y^2},\frac{1} {1/\sigma_x^2+1/\sigma_y^2}) (x,y)∼N(σx2+σy2μyσx2+μxσy2,1/σx2+1/σy21) 具体的推导方式,可以通过 p ( x ) p ( y ) p(x)p(y) p(x)p(y)乘积获得: p ( x ) p ( y ) = 1 2 π 2 σ x σ y exp ( − σ y 2 ( x − μ x ) 2 + σ x 2 ( x − μ y ) 2 2 σ x 2 σ y 2 ) p(x)p(y)=\frac {1} {2\pi^2\sigma_x\sigma_y} \exp (-\frac {\sigma_y^2(x-\mu_x)^2 + \sigma_x^2(x-\mu_y)^2} {2\sigma_x^2\sigma_y^2}) p(x)p(y)=2π2σxσy1exp(−2σx2σy2σy2(x−μx)2+σx2(x−μy)2) 通过将 e x p exp exp中的 ( σ x 2 + σ y 2 ) x 2 (\sigma_x^2+\sigma_y^2)x^2 (σx2+σy2)x2和常数项凑平方后,能够得到一个形似 λ 1 2 π σ exp [ − ( x − μ ) 2 2 σ 2 ] \ \lambda \frac {1} {\sqrt {2\pi}\sigma} \exp [ - \frac {(x-\mu)^2}{2\sigma^2}] λ2π σ1exp[−2σ2(x−μ)2],只不过系数 λ \lambda λ的存在使得这个函数的积分不等于1。 具体的证明可以参照这个Blog: 两个高斯分布乘积的理论推导 版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 本文链接:https://blog.csdn.net/chaosir1991/article/details/106910668/ python示意图
如果 X = [ x 1 , x 2 , … , x n ] T X=[x_1,x_2,\dots,x_n]^T X=[x1,x2,…,xn]T是个服从高斯分布的多维随机变量,可以记为 X ∼ N ( μ , Σ ) X\sim N(\mu, \Sigma) X∼N(μ,Σ),其中 μ = [ μ 1 , μ 2 , … , μ n ] T \mu=[\mu_1,\mu_2,\dots,\mu_n]^T μ=[μ1,μ2,…,μn]T, Σ ∈ R n × n \Sigma \in \R^{n\times n} Σ∈Rn×n是各分量的协方差矩阵。 概率密度函数可表示为: p ( X ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − ( X − μ ) T Σ − 1 ( X − μ ) 2 ) p(X)=\frac {1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp (-\frac {(X-\mu)^T\Sigma^{-1}(X-\mu)}{2}) p(X)=(2π)n/2∣Σ∣1/21exp(−2(X−μ)TΣ−1(X−μ)) 多维高斯分布有一个比较重要的性质: 对于多维高斯分布 X ∈ R n X\in \R^n X∈Rn,经过线性变换 A ∈ R k × n A\in \R^{k\times n} A∈Rk×n, Y = A X ∈ R k Y=AX\in \R^k Y=AX∈Rk仍然是一个多维高斯分布,且 Y ∼ N ( A μ , A Σ A T ) Y\sim N(A\mu,A\Sigma A^T) Y∼N(Aμ,AΣAT) 此外,两个多维高斯分布概率密度函数的乘积,仍然具有多维高斯分布概率密度函数的形式。 五、共轭分布贝叶斯定理有: p ( x ∣ z ) = p ( z ∣ x ) p ( x ) p ( z ) ∝ p ( z ∣ x ) p ( x ) p ( x ) i s p r i o r p ( x ∣ z ) i s p o s t e r i o r p ( z ∣ x ) i s l i k e l i h o o d p(x|z)=\frac {p(z|x)p(x)}{p(z)} \propto p(z|x)p(x) \\ p(x)\ is \ prior \\ p(x|z)\ is \ posterior \\ p(z|x)\ is \ likelihood p(x∣z)=p(z)p(z∣x)p(x)∝p(z∣x)p(x)p(x) is priorp(x∣z) is posteriorp(z∣x) is likelihood 如果后验分布和先验分布是同类型的分布,则称先验分布和后验分布是共轭分布,先验分布是似然的共轭先验。 根据高斯分布的特性,如果先验和似然都是高斯分布的形式,那么它们是共轭的。 后记在这里记录一个二维正态分布的充要条件: ( x , y ) (x, y) (x,y)服从二维正态分布,当且仅当 x x x和 y y y的任意线性组合均服从一维正态分布。 |
【本文地址】
今日新闻 |
推荐新闻 |
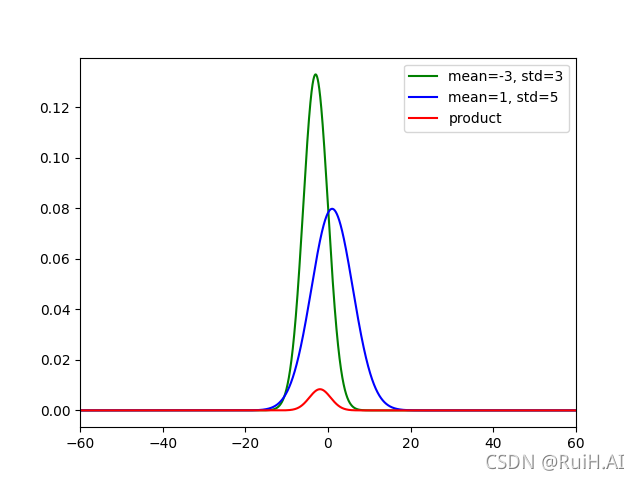 红色函数是蓝绿两个高斯分布的乘积结果,可以看出其形状也是对称的,但与x轴围成的面积少于另外两个高斯分布。
红色函数是蓝绿两个高斯分布的乘积结果,可以看出其形状也是对称的,但与x轴围成的面积少于另外两个高斯分布。