设为首页收藏本站
开启辅助访问

离散数学·欧拉图、哈密顿图、无向树和生成树

 您所在的位置：网站首页 › 欧拉图的画图题 › 离散数学·欧拉图、哈密顿图、无向树和生成树

离散数学·欧拉图、哈密顿图、无向树和生成树

2023-08-28 13:24| 来源: 网络整理| 查看: 265

欧拉图

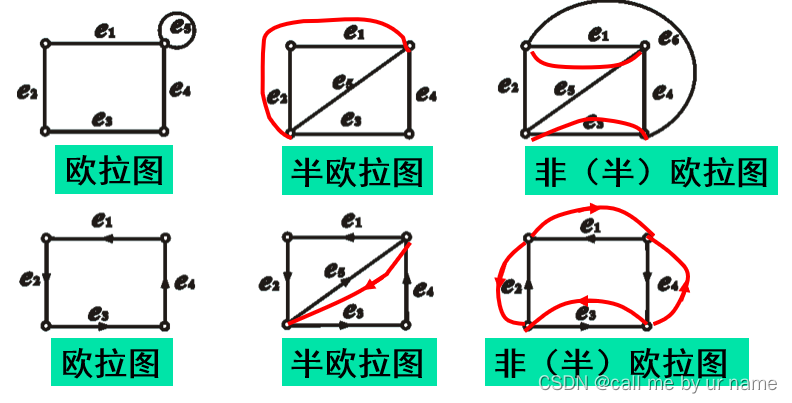在这里插入图片描述 简而言之——欧拉图就是边不能重复（点可以），还要有回路的图（可以类比成能否用一条线画完这个图，且线经过的路是不重复的） 半欧拉图就是非欧拉图（有欧拉通路，但没有欧拉回路：能经过所有的边，但最后回不到起点） 在这里插入图片描述 有向图的话就要注意一下，方向

定理

在这里插入图片描述

欧拉图要求所有顶点都是偶数度，也比较容易明白：当出现奇数度顶点时，没办法抵消掉，所以一定会出现一条边走过2次

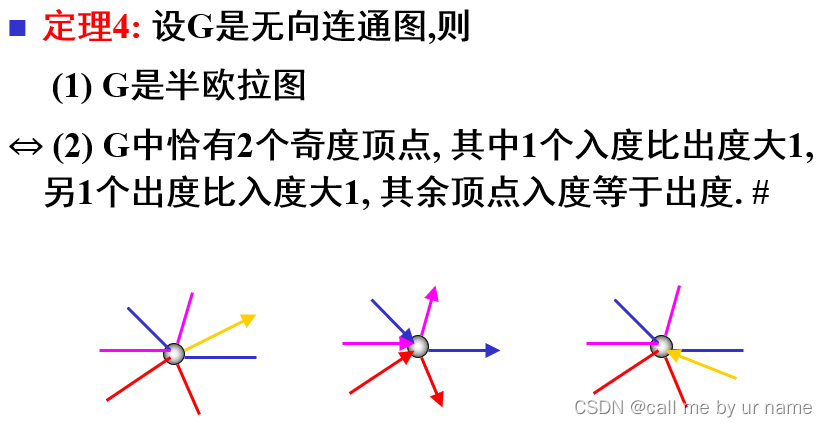
在这里插入图片描述

在这里插入图片描述 在这里插入图片描述

哈密顿图

在这里插入图片描述 经过所有点，并且点不重的回路

定理

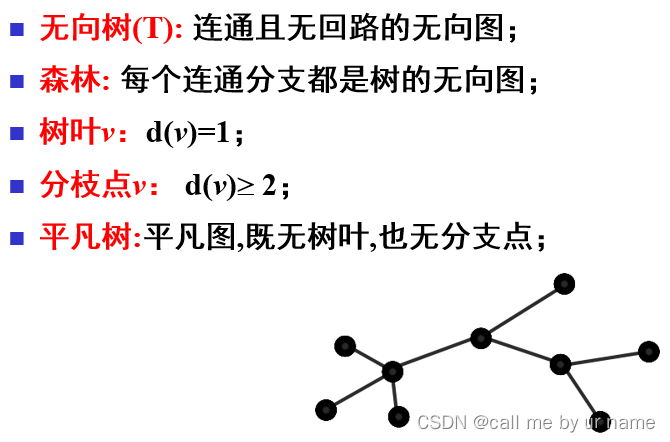在这里插入图片描述 p(G-V’)指连通分支数 这个定理相对来说比较重要一些：用来判定非哈密顿图 看看，理解一下 在这里插入图片描述 这里是半哈密顿图，所以+1 注意以上2个定理都是无向 以上都为必要条件 在这里插入图片描述 充分条件 在这里插入图片描述

例

在这里插入图片描述

无向树

在这里插入图片描述 连通无回路——树

性质

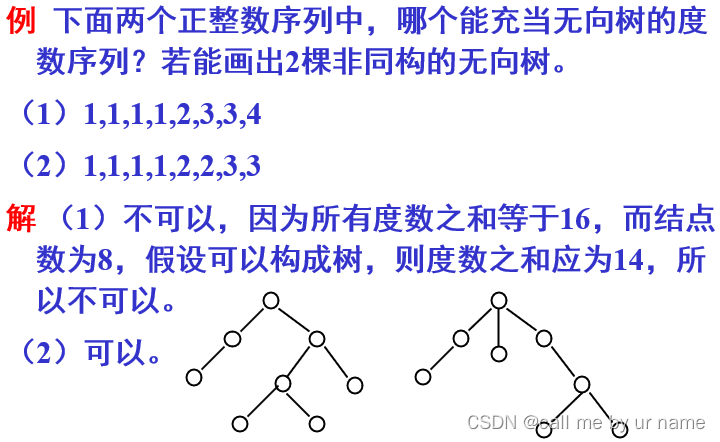在这里插入图片描述

m=n-1

例

在这里插入图片描述 在这里插入图片描述 证明较简单，看看就行了 在这里插入图片描述 握手定理 ∑d(v)=2m=2(n-1)（仅限于树有2(n-1)）

生成树

在这里插入图片描述 生成子图——点集与原来的图点集一样 图G，T是G的生成子图，并且T是树。那么T是生成树2023.2.12复习

定理

在这里插入图片描述

印象中这个定理用得好像还挺多的 无向图G连通当且仅当有生成树

在这里插入图片描述

在这里插入图片描述

这个证明可以浅看一下

在这里插入图片描述

基本回路

在这里插入图片描述 简而言之——生成树+一条弦得到的图中有一个圈（小圈就行不一定需要生成树所有的边 2023.2.12复习），就称为基本回路 基本回路系统数量m-n+1 求基本回路系统时，枚举每条边来求 每条弦对应唯一

基本割集系统

在这里插入图片描述 割集是对G来说的 简而言之——只能有一条树枝，其余全是弦（但不是所有的弦） 基本割集系统数量n-1 每条树枝对应唯一

例

在这里插入图片描述

C表示圈（一部分或者全部树枝+1条弦） S表示割集（一部分或者全部弦+1条树枝）

G的生成树的个数

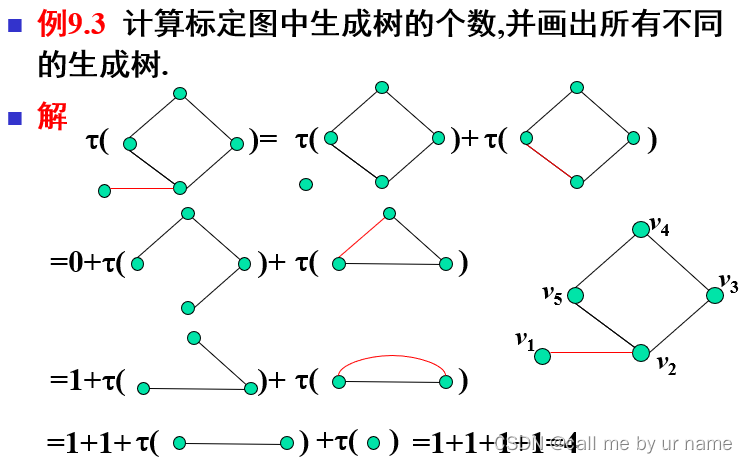在这里插入图片描述 这个符号是生成树个数的意思2023.2.12复习 G\e表示在G中收缩e G-e就是删掉e这条边 在这里插入图片描述 不连通——生成树个数为0 收缩的意思就是将这条边变为透明的，但是其仍然存在。或者说，理解为字面意思“收缩”，将这条边收缩至无法可视，并且边关联的点也因为边的收缩而产生移位、重合 收缩完之后，平行边要保留

练习（作业） 3

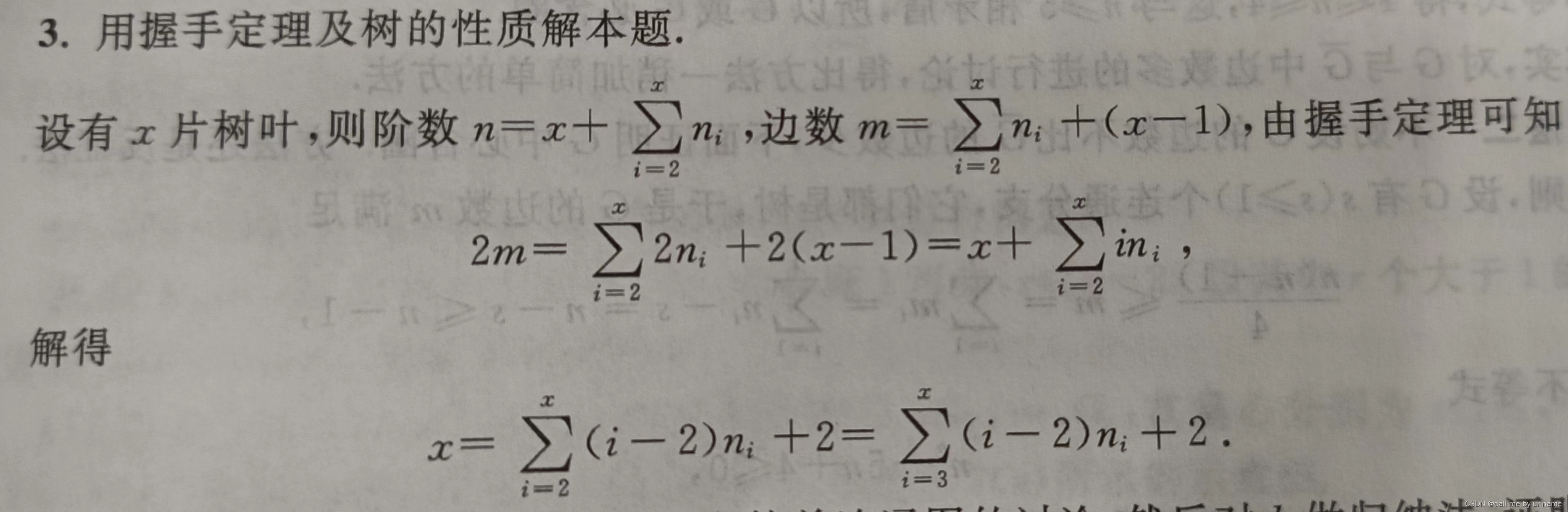在这里插入图片描述 在这里插入图片描述 比较经典的题目，难度不大，但充分利用了握手定理，值得看看

5

在这里插入图片描述 标准答案： 在这里插入图片描述 我的答案： 在这里插入图片描述 没什么好说的，比较正常的一道证明题，难度不大

12

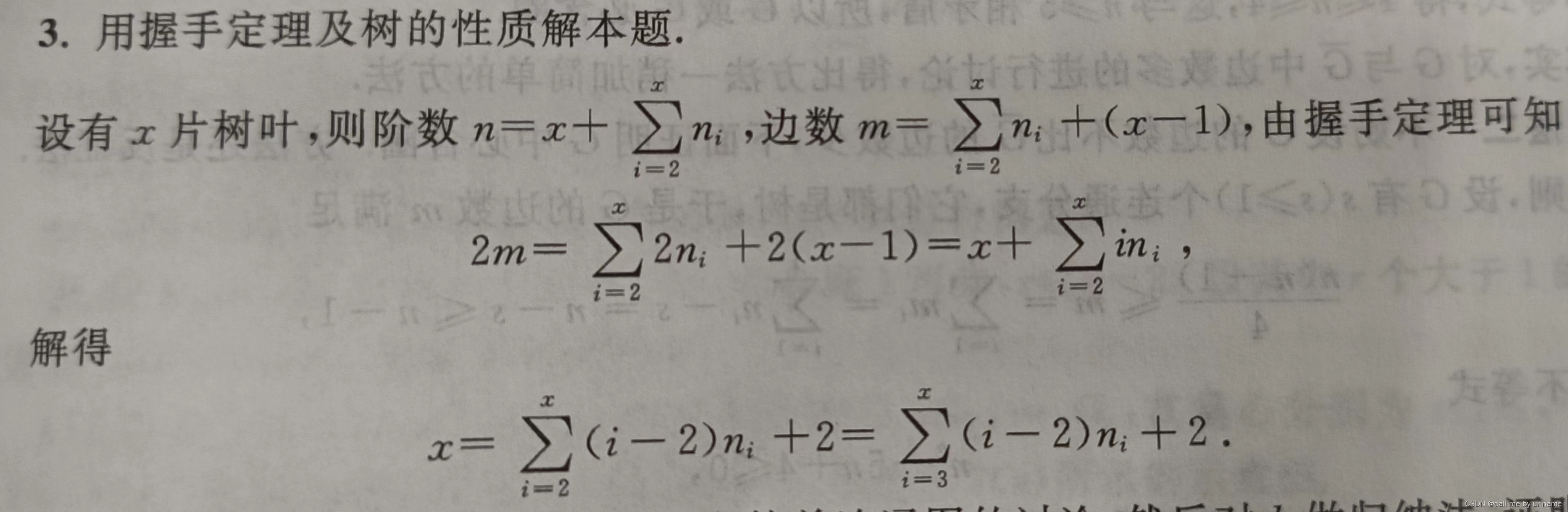在这里插入图片描述 标准答案 在这里插入图片描述 我的答案 在这里插入图片描述 在这里插入图片描述 题目意思也表示很难，但是证明过程值得一看



【本文地址】


今日新闻

推荐新闻

CopyRight 2018-2019 办公设备维修网 版权所有 豫ICP备15022753号-3