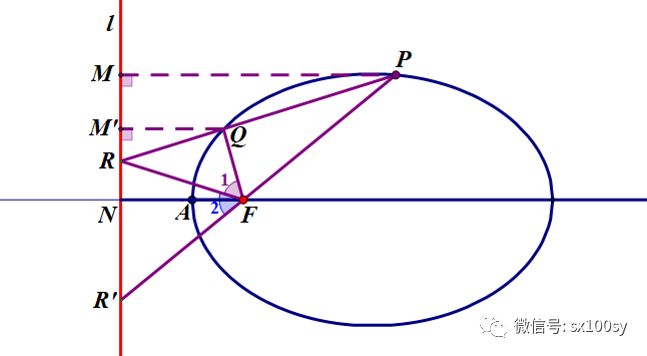
证明：

（1）分别过点P和Q作准线l的垂线，设垂足分别为M和M'。于是，根据椭圆焦点、准线的定义，FQ/M'Q=FP/MP，即FQ/FP= M'Q/MP。又因为三角形RQM'与三角形RPM相似，所以M'Q/MP = RQ/RP。所以由这两个比式，得出：

FQ/ FP = RQ / RP

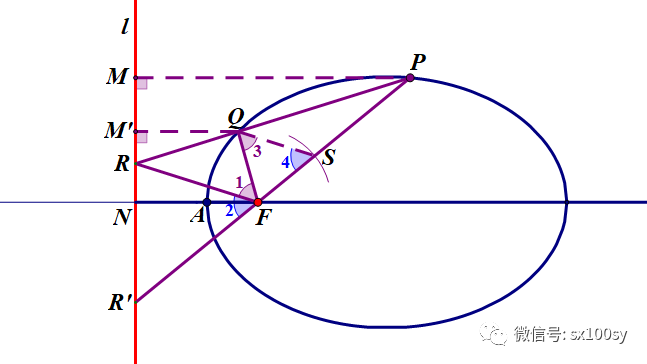
（2）如下图所示。以F为圆以，以FQ为半径作圆，与FP交于点S。连接QS。所以FQ=FS。代入上面所得的比例式，得：

FS / FP = RQ / RP

这说明

三角形PQS 与 三角形PRF 相似

所以

QS ∥ RF

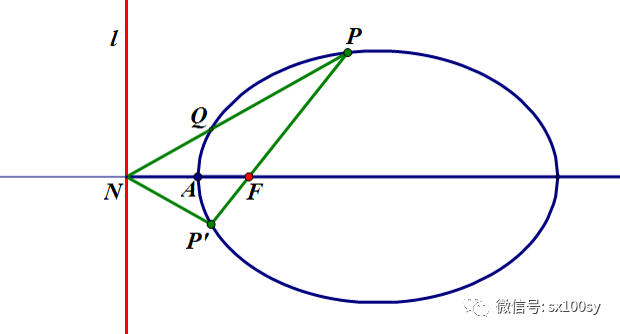
从而有

∠1 = ∠3， ∠2 = ∠4

而三角形FQS为等腰三角形（因为FQ=FS），所以

∠3=∠4

所以

∠1=∠2

即FR平分∠QFR'

（三）焦点弦的相关性质（1）

如下图所示。PP'为椭圆的焦点弦（过焦点的弦）。连接PN和P'N。则轴线平分角PNP'。

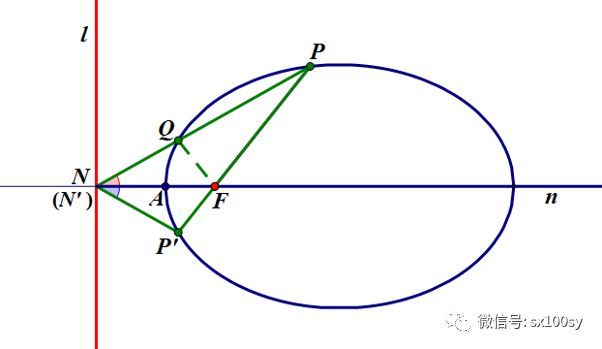
证明：

如下图所示。如果P与P'两点关于轴是对称的点，那么显然角PNP'被轴线所平分。下面不妨设FP>FP'。在椭圆上找到点P'关于轴线对称的点Q。连接PQ，并延长，与准线相交于点N'。那么，由上一条所讲的性质，FN' 平分∠QFP'。因点Q和P'关于轴线对称，所以，过焦点F且平分角QFP'的直线就是轴线。所以，点N'就是点N。PN'就是PN。再次利用点Q与点P'关于轴线对称这一条件，就得到

∠QNF = ∠P'NF（图中红色角=蓝色角）

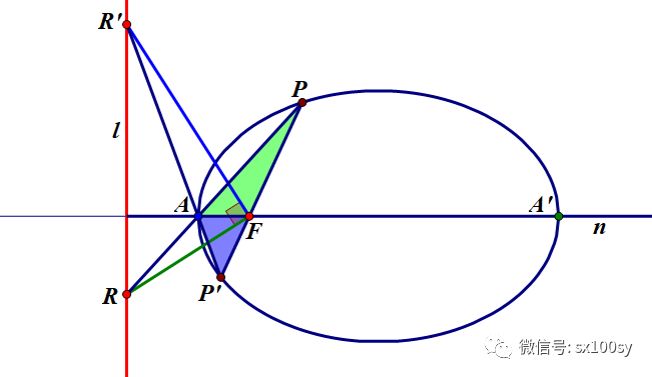
即轴线n平分角PNP'。也就是说，分别连接焦点弦两个端点与点N所得到的两条线段，它们构成的夹角被轴线所平分。即n平分∠QNP' 。也可以说，若把准线设想为一个与椭圆所在面垂直的平面镜，那么，从焦点弦一个端点发出的光，照射到准线与轴线的交点后，经镜面反射，光线一定会照射到焦点弦的另一个端点。

（四）焦点弦的相关性质（2）

PP'为椭圆的焦点弦。焦点为F，椭圆靠近准线的顶点为A。连接PA并延长，与准线交于点R; 连接P'A并延长，与准线交于点R'。连接FR，连接FR'。则三角形RFR'为直角三角形，其中直角位于点F处。

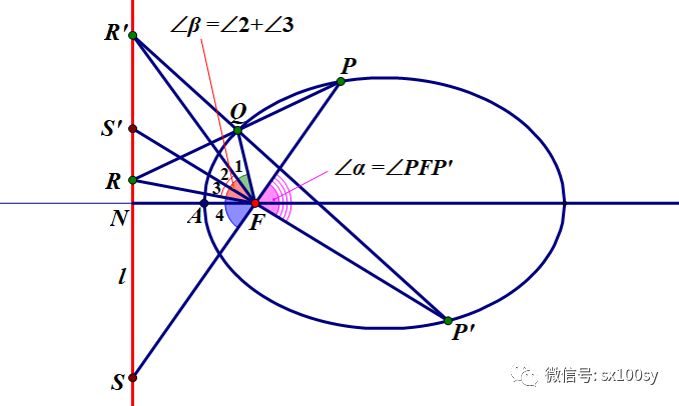
证明不难。仍然是利用前面那个基本性质。用两次。FR和FR'分别是三角形PAF和P'AF在点F处的外角平分线。观察图形，相信您自己应该能看出来的。

另外，观察上图，问您，R'，P，A'这三点共线吧？答案是共线，因为FR'也是三角形FPA'角F处外角的平分线。同理，R，P'，A'这三点也共线。所以，我们有一个推论：焦点弦一端点和椭圆一顶点的连线与焦点弦另一端点和椭圆另一顶点的连线在准线上交汇。

（五）

有椭圆的两条弦PQ和P'Q，它们有一个公共端点Q。分别延长PQ和P'Q，与准线分别交于点R和R'。连接FR，连接FR'。则有下面的角的关系成立：

∠PFP' = 2∠RFR' （∠α = 2∠β）

证明：也很简单。延长PF与准线交于点S；延长P'F与准线交于点S'。于是有

∠α= ∠PFP'

= ∠3 +∠4（对顶角相等）

= ∠3 +（∠1+∠2+∠3 ）（因为FR平分∠QFS）

= 2∠3 +（∠1+∠2 ）

= 2∠3 + 2∠2（因为FR'平分∠QFS'，有∠1=∠2）

=2（∠3 + ∠2）

= 2∠β

相信看到这里的您，一定收获不小！那就给点个“好看“吧。返回搜狐，查看更多