矩阵的极限与马尔科夫链(上) |
您所在的位置:网站首页 › 根据转移概率矩阵求分布概率 › 矩阵的极限与马尔科夫链(上) |
矩阵的极限与马尔科夫链(上)
|
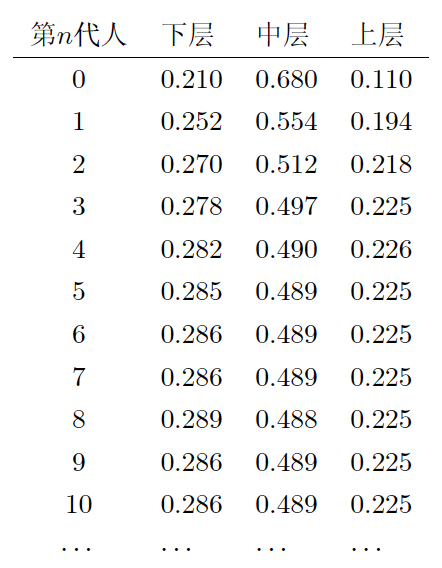
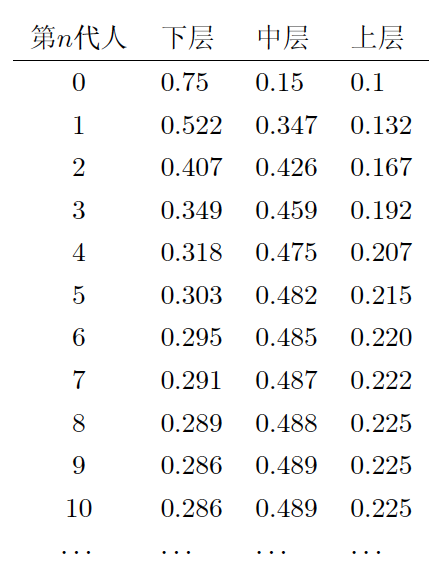
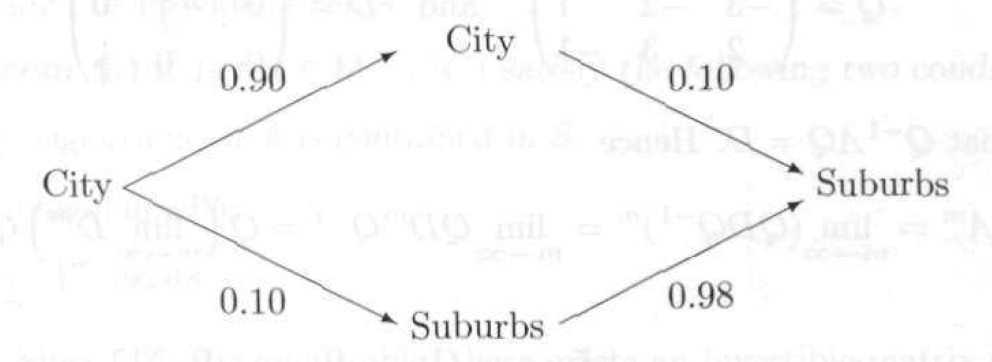
〇、引言 工欲善其事必先利其器。机器学习、数据挖掘、自然语言处理等等学科与数学结合非常紧密,要想真正理解这些课程中的诸多细节,势必要把数学基础打牢。管中窥豹,可见一斑。我们今天就来谈谈和马尔科夫链有关的一些数学知识。 听到“马尔科夫”你会想到机器学习中的什么内容?嗯,或许你会想到HMM(隐马尔科夫模型),又或者MCMC(马尔科夫链蒙特卡洛)。文献【2】中整理了LDA(Latent Dirichlet Allocation)主题词模型中所涉及到的诸多数学问题,其中就谈到了MCMC,而要理解MCMC,首先要知道马尔科夫链以及矩阵的极限这些知识。接下来我们就从数学的源头来一探究竟。 一、Begin with an example 我们先来看一个文献【2】中给出的例子。社会学家经常把人按其经济状况分成3类:下层(lower_class)、中层(middle-class)、上层(upper-class),我们用1,2,3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别,那么他的孩子属于下层收入的概率是0.65,属于中层收入的概率是0.28,属于上层收入的概率 是 0.07。事实上,从父代到子代,收入阶层的变化的转移概率如下 使用矩阵的表示方式,转移概率矩阵记为 假设当前这一代人处在下层、中层、上层的人的比例是概率分布向量π0= [ π0(1),π0(2)。π0(3)],那么他们的子女的分布比例将是π1=π0P,他们的孙子代的分布比例将是π2= π1P=π0P2, …., 第 n 代子孙的收入分布比例将是πn= πn-1P=π0Pn, ….。假设初始概率分布为π0 =[0.21,0.68, 0.11],则我们可以计算前 n 代人的分布状况如下 我们发现从第7代人开始,这个分布就稳定不变了,这个是偶然的吗?我们换一个初始概率分布π0 = [0.75, 0.15, 0.1] 试试看,继续计算前 n 代人的分布状况如下 我们发现,到第9代人的时候,分布又收敛了。最为奇特的是,两次给定不同的初始概率分布,最终都收敛到概率分布π = [0.286,0.489,0.225],也就是说收敛的行为和初始概率分布π0无关。这说明这个收敛行为主要是由概率转移矩阵P决定的。我们计算一下Pn, 我们发现,当n足够大的时候,这个Pn矩阵的每一行都是稳定地收敛到π = [0.286, 0.489, 0.225] 这个概率分布。自然地,这个收敛现象并非是我们这个例子所独有,而是绝大多数“马尔科夫链”的共同行为(后续我们会再来具体说明马尔科夫链的概念)。 二、Another Instance 为了求得一个理论上的结果,我们来看一个更小规模的例子(这将方便我们后续的计算演示),假设在一个区域内,人们要么是住在城市,要么是住在乡村。下面的矩阵告诉我们人口迁移的一些规律(或倾向)。例如,第1行第一列就表示,当前住在城市的人口,明年将会有90%的人选择继续住在城市。 作为一个简单的开始,试着来计算一下现今住在城市的人中2年后会住在乡村的几率有多大。分析可知,当前住在城市的人,1年后,会有90%继续选择住在城市,另外10%的人则会搬去乡村居住。然后又过了1年,上一年中选择留在城市的人中又会有10%的人搬去乡村。而上一年中搬到乡村的人中将会有98%的选择留在乡村。这个分析过程如下图所示,最终可以算出现今住在城市的人中2年后会住在乡村的几率=0.90×0.10+0.10×0.98。 其实你会发现我们的计算过程就是在做矩阵的平方。如下图所示,你会发现结果矩阵中第2行第1列的计算就是在执行上面在处理的操作。在此基础,我们还可以继续计算n年后的情况,也就是计算矩阵A自乘n次后的结果。 如果我们假设最开始的时候,城乡人口的比例为7:3,那么我们可以用一个列向量来表示它 P=[0.7, 0.3]T,我们想知道最终城乡人口的比例为何,则就是要计算 三、Three Concepts 我们来辨析三个概念:随机过程、马尔科夫过程、马尔科夫链。这三个概念中,都涉及到object和它们对应的state这两个要素。在刚刚给出的例子中,研究的object就是人,人的state分为住在城市或者住在乡村两种。 Stochastic process: a process where elements of a set are each classified as being in one of several fixed states that can switch over time by a probability.Markov process: a stochastic process with the property that, given the present state, the present and past states are independent.Markov chain: The Markov process with the finite possible states.最宽泛的概念就是随机过程,限制最多的就是马尔科夫链。对于马尔科夫链,必须满足两个条件:1)当前状态仅跟上一个状态有关;2)总共的状态数是有限的。如果状态数可以是无限多个,那样的问题就称为Markov process。但在Markov process中我们仍然要求,时间是离散的,例如我们的例子是以“年”为单位的。如果时间允许是连续的,那样的问题就称为Stochastic process。本文仅仅讨论马尔科夫链。 在某个时间点上,object的状态为s1,下一个时刻,它的状态以某种概率转换到其他状态(也包含原状态s1),这里所说的“以某种概率转换”最终是通过转移矩阵(或称随机矩阵)的形式来给出的。转移矩阵的定义如下: 此外,a transition matrix is called regular if some power of the matrix contains only positive entries.(其中 “some” 的意思就是 存在一个整数 n 使得 (An)ij>0 for all i, j) 所以从状态转移矩阵中,(结合之前的两个例子)我们可以看出Aij元素给出的信息就是(在一个单位时间间隔内)object从状态 j 转移到状态 i 的概率。Let P=(p0, p1, ..., pn)T be a vector, then P is called a probability vector if pi>=0 for all i and ∑pi=1。所以你可以看出,任意一个转移矩阵中的某一列都是一个概率向量(probability vector)。 四、一个重要的定理 这个定理非常非常奇妙的地方就是它给出了之前困惑我们的问题的答案!我们的问题是:如果假设最开始的时候,城乡人口的比例为7:3,那么我们可以用一个列向量来表示它 P=[0.7, 0.3]T,我们想知道最终城乡人口的比例为何,则就是要计算 在证明这个定理之前,不妨先来用之前给出的例子来验证一下这个定理。注意到如果要计算 于是可知矩阵A的对角化结果如下: 所以有 然后把值带进去就能算出最终结果如下 之前我们已经算过特征值1对应的一个特征向量是[1, 5]T,特征向量乘以一个系数仍然是特征向量(注意我们要求最后的特征向量同时是一个概率向量,所以会得到[1/6, 5/6]T),可见上述计算与定理所揭示的结果是完全一致的。 五、证明定理5.20的一些准备 为了深刻揭示Thm 5.20 所给出之结果的原由,我们还需做几个准备工作。这部分讨论仅对希望深入研究原理的朋友有意义,如果你只是想知道结论,或者至少需要停留在应用层面,你可以跳过这部分内容。 Thm 5.16 (Gerschgorin's Disk Theorem): (注释:这是一个用来对矩阵特征值进行估计的定理。这个定理的意思是,在复平面上造圆,以矩阵对角线上的元素Akk为圆心,半径则是圆心同一行的其他元素的绝对值之和。) If λ is an 特征值 of A , then 下面是应用圆盘定理的一个例子: 除了圆盘定理以外,我们还有如下结论可以用于估计矩阵特征值的上限。 例如: (为避免文章过长,特将其拆解成两个部分。本部分内容到此为止,请关注《矩阵的极限与马尔科夫链(下)》) 本文主要根据台湾交通大学开放课程线性代数(莊重 特聘教授主讲)之授课内容整理,并参考以下文献: 【1】S.H. Friedberg, A.J. Insel, L.E Spence, 4th edition, Linear Algebra, Prentice-Hall, 2003 【2】靳志辉,LDA数学八卦,2013 |
【本文地址】
今日新闻 |
推荐新闻 |
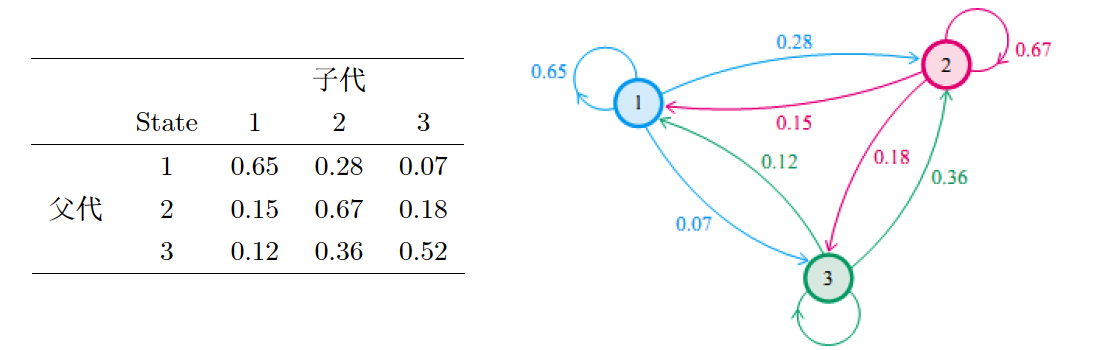
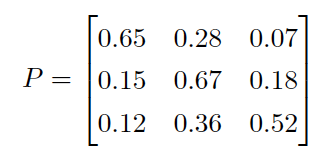
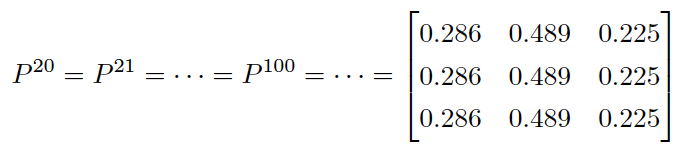



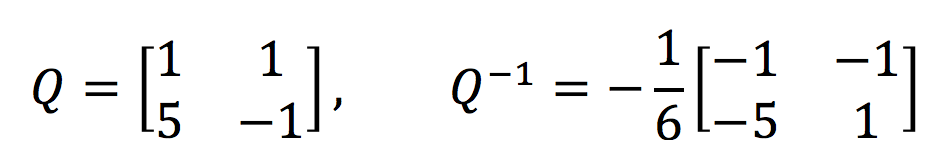
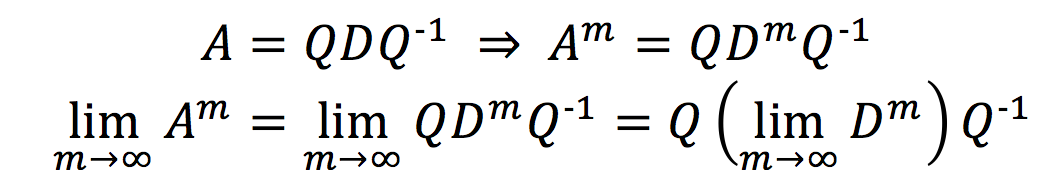
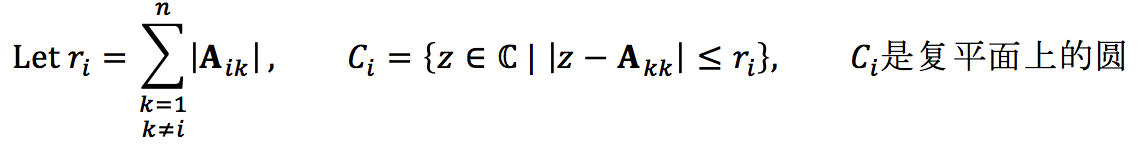
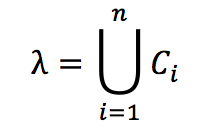 (也就是说,λ一定位于上述几个圆中的某一个里面)
(也就是说,λ一定位于上述几个圆中的某一个里面)