写在最前面：先说清楚，该法由海明大佬@未灬秋色原创，大家若想更加深入了解，可浏览专栏“海明的放缩笔记”

下周一复课，更新量就少了，见谅~

顺便安利一下一位大佬：

@热爱代数的好学生

这个定义是直接从几何直观上得来的。如果在曲线弧上面任意取两点，连接这两点的弦总是在弧段的上方，那么曲线就是（向上）凹的，反之也有可类比的结论。取一个特殊的点，即弦的中点，曲线的凹凸性可以用弦的中点与曲线弧上具有相同坐标的点的位置关系来描述。

不过补充一下，中国数学界关于函数凹凸性定义和国外很多定义是反的。国内教材中的凹凸，是指的函数图像形状，而不是指函数的性质。在国外，图像的凹凸与直观感受一致，却与函数的凹凸性相反。

（这对于数学小白的我当然无关啦~）

我们还需要掌握一个运算更加简便的判定定理：

高中常考的函数便是这两张脸： e^x 和 ln x ，而他们的凹凸性很“显然”。

所以我们需要了解一些相关的图像，便于接下来的转化。

第一个： f(x)=xlnx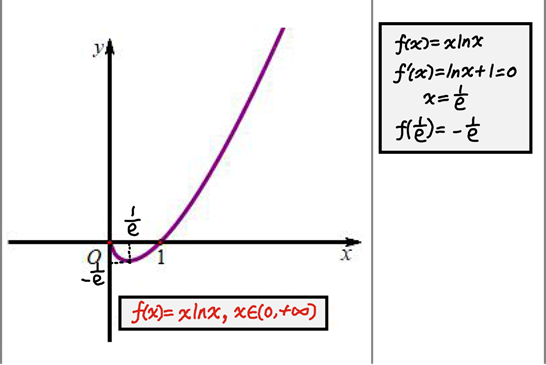

第二个： f(x)=\frac{x}{lnx}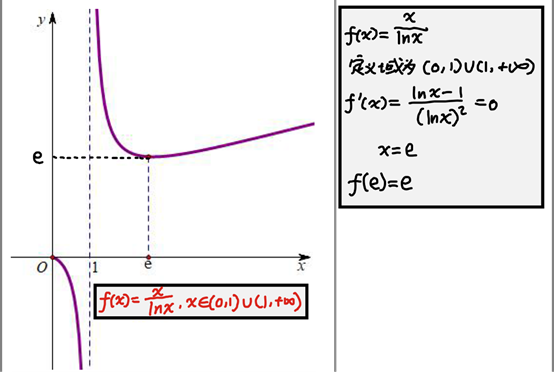

第三个： f(x)=\frac{lnx}{x}

第四个： f(x)=xe^x

第五个： f(x)= \frac{x}{e^x}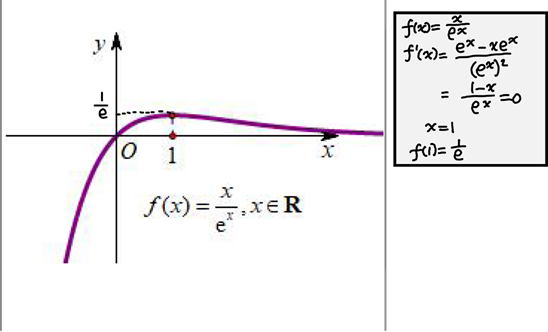

第六个： f(x)= \frac{e^x}{x}

证明不等式问题中有一类不等式形式复杂，由即首先知道两个函数(其中一个常常是对数函数与多项式函数的组合，另一个则是指数函数与多项式函数的组合)组合而成，我们往往指对分离，然后研究函数的图像，两个函数图像凹凸性刚好相反，称凹凸反转，这个名词非常形象的阐述了这类题目的解题思想。