|
matlab编译平面有限元计算(附有完整代码)
完整代码下载链接 点击此处下载哦 下载后运行‘main.m’即可
问题描述 使用完成的代码,解决图1所示的平面应力问题。中心孔半径为A的均匀薄板承受单轴应力。a=0.5 in.,h=3 in.,w=6 in.,E=10(10)6 psi,泊松比=0.3。计算应力分布。 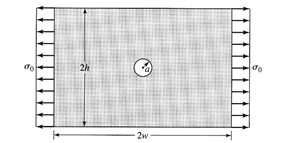 1. 模型绘制与网格划分 此问题第一步需要解决的就是网格的划分,模型绘制可以使用Matlab自带的矩形和圆工具,对于网格的划分,以一种较为简单的方式进行,这样也可以减低一些编程难度,效果如图所示,我全部使用三角形单元,对于中间的圆形孔洞,圆形的网格划分在程序上存在一定难度,我用方形空洞代替,在划分网格的同时,对于节点的编号和坐标将其记录在一个Node_information矩阵中,对于三角形单元的编号和包含的节点保存在Element_information中。(此部分对应的程序为Meshing.m) 1. 模型绘制与网格划分 此问题第一步需要解决的就是网格的划分,模型绘制可以使用Matlab自带的矩形和圆工具,对于网格的划分,以一种较为简单的方式进行,这样也可以减低一些编程难度,效果如图所示,我全部使用三角形单元,对于中间的圆形孔洞,圆形的网格划分在程序上存在一定难度,我用方形空洞代替,在划分网格的同时,对于节点的编号和坐标将其记录在一个Node_information矩阵中,对于三角形单元的编号和包含的节点保存在Element_information中。(此部分对应的程序为Meshing.m)
 2. 单元刚度矩阵的建立与整体刚度矩阵装配 得到单元信息和节点信息之后,下面的操作类似于桁架的有限元分析,需要建立每一个单元对应的刚度矩阵,对于三角形单元来说,课件中有详细的说明,其核心利用到的公式如下: 下面我们将公式转化为代码语言,D矩阵比较容易书写,B矩阵则要利用上步储存的Node_information和Element_information,通过矩阵的索引准确的找到每个三角形单元对应的节点坐标,再通过矩阵乘法则可以得到每个单元的刚度矩阵(66)。 为了利于后续的装配,我们将每个单元的刚度矩阵赋值到一个‘小装配矩阵’,此矩阵含义为把一个(66)矩阵按照公式1规则装配到一个(2*节点总数)的方阵中,此规则不同于桁架结构,因为其刚度矩阵是按照(u1 u2 u3 v1 v2 v3)的顺序来生成的,对应的匹配规则也要得到调整。(完成此部的程序文件对应为Single_triangular.m) 2. 单元刚度矩阵的建立与整体刚度矩阵装配 得到单元信息和节点信息之后,下面的操作类似于桁架的有限元分析,需要建立每一个单元对应的刚度矩阵,对于三角形单元来说,课件中有详细的说明,其核心利用到的公式如下: 下面我们将公式转化为代码语言,D矩阵比较容易书写,B矩阵则要利用上步储存的Node_information和Element_information,通过矩阵的索引准确的找到每个三角形单元对应的节点坐标,再通过矩阵乘法则可以得到每个单元的刚度矩阵(66)。 为了利于后续的装配,我们将每个单元的刚度矩阵赋值到一个‘小装配矩阵’,此矩阵含义为把一个(66)矩阵按照公式1规则装配到一个(2*节点总数)的方阵中,此规则不同于桁架结构,因为其刚度矩阵是按照(u1 u2 u3 v1 v2 v3)的顺序来生成的,对应的匹配规则也要得到调整。(完成此部的程序文件对应为Single_triangular.m)
function [K,B,D]=Single_triangular(Num_node,Node_sum,E,Poisson)
%Node_sum 是3*3表示三角形三个节点坐标 前一个是编号 后两个是坐标
K=zeros(2*Num_node);
A=0.5*abs(det([1 Node_sum(1,2) Node_sum(1,3);...
1 Node_sum(2,2) Node_sum(2,3);1 Node_sum(3,2) Node_sum(3,3)]));
B=(1/(2*A))*[Node_sum(2,3)-Node_sum(3,3) Node_sum(3,3)-Node_sum(1,3) Node_sum(1,3)-Node_sum(2,3) 0 0 0;...
0 0 0 Node_sum(3,2)-Node_sum(2,2) Node_sum(1,2)-Node_sum(3,2) Node_sum(2,2)-Node_sum(1,2);...
Node_sum(2,3)-Node_sum(3,3) Node_sum(3,3)-Node_sum(1,3) Node_sum(1,3)-Node_sum(2,3)...
Node_sum(3,2)-Node_sum(2,2) Node_sum(1,2)-Node_sum(3,2) Node_sum(2,2)-Node_sum(1,2)];
D=(E/(1-Poisson^2))*[1 Poisson 0;Poisson 1 0;0 0 (1-Poisson)/2];
k=A*B'*D*B;
list=[Node_sum(1,1) Node_sum(2,1) Node_sum(3,1) ...
Num_node+Node_sum(1,1) Num_node+Node_sum(2,1) Num_node+Node_sum(3,1)];
for i =1:6
for j =1:6
K(list(i),list(j))=k(i,j);
end
end
end
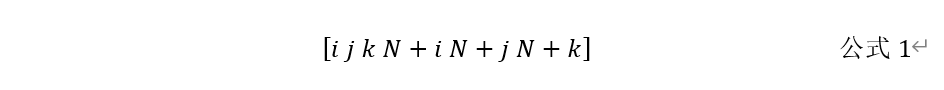 由于得到了‘小装配矩阵’,接下来对每个三角形单元得到的‘小装配矩阵’作累加即可,这里只需要对Element_information遍历即可。完成此部的程序文件对应为Assemble.m) 由于得到了‘小装配矩阵’,接下来对每个三角形单元得到的‘小装配矩阵’作累加即可,这里只需要对Element_information遍历即可。完成此部的程序文件对应为Assemble.m)
function [KK,B,D]=Assemble(Node_information,Element_information,E,Poisson)
Num_node=size(Node_information,1);
Num_element=size(Element_information,1);
KK=zeros(2*Num_node);
B=[];
for i =1:Num_element
Node_sum=[Element_information(i,2) ...
Node_information(Element_information(i,2),2) ...
Node_information(Element_information(i,2),3);...
Element_information(i,3) ...
Node_information(Element_information(i,3),2) ...
Node_information(Element_information(i,3),3);...
Element_information(i,4) ...
Node_information(Element_information(i,4),2) ...
Node_information(Element_information(i,4),3)];
[K,b,D]=Single_triangular(Num_node,Node_sum,E,Poisson);
B=[B;b];
KK=KK+K;
end
end
3. 外载转化至节点 在本题目中,板子两侧受到均布外载,我们需要将其转化到节点上,主要利用对形函数的积分上,其核心如公式2和所示,对于本题而言是均布荷载,简单的笔算可以得到节点的等效力,编程这里就直接给出。(对应程序文件为Load_plane.m)
 4. 求解节点位移 经过上几步的准备工作,已经得到了刚度K矩阵和外载F矩阵,只需要对K求逆再与F相乘就可以得到结果了。但此时存在一个问题,对于刚度矩阵数量较为庞大,很容易出现矩阵接近奇异值的情况,Matlab处理此问题较为强大,提供了四种求逆的方法。如下表所示: 4. 求解节点位移 经过上几步的准备工作,已经得到了刚度K矩阵和外载F矩阵,只需要对K求逆再与F相乘就可以得到结果了。但此时存在一个问题,对于刚度矩阵数量较为庞大,很容易出现矩阵接近奇异值的情况,Matlab处理此问题较为强大,提供了四种求逆的方法。如下表所示:
表1 求逆方法一览表
方法 介绍 Inv(K)*F 直接求逆,对于病态矩阵产生很大错误 Pinv(K)*F 伪逆,较为准确 K\F 高斯消主元,结果误差较大 Lsqminnorm(K,F) 最小范数,最为准确 ————————————————————————
通过最小范数求得的结果较为准确,如表2展示的是四种方法得到的结果(前301个节点x方向位移)。由于计算出的位移非常小,下图是我将位移扩大1000倍展示的位移图,如图3,红色虚线为变形后图形。为了对比保证结果准确性,我们使用Ansys建模分析,得到图4,两者大致一样。(对应程序文件为Output_plane_displacement.m)
表2 不同算法结果
Lsqminnorm(K,F) Inv(K)*F Pinv(K)*F K\F -6.1616E-04 -4.9019E-04 -6.1616E-04 -5.7071E-04 -6.1704E-04 -4.8256E-04 -6.1704E-04 -5.7158E-04 -6.1815E-04 -4.7112E-04 -6.1815E-04 -5.7268E-04 -6.1943E-04 -4.7684E-04 -6.1943E-04 -5.7395E-04 -6.2066E-04 -4.6921E-04 -6.2066E-04 -5.7517E-04 -6.2161E-04 -4.6539E-04 -6.2161E-04 -5.7611E-04 -6.2209E-04 -4.5013E-04 -6.2209E-04 -5.7657E-04 -6.2204E-04 -4.5013E-04 -6.2204E-04 -5.7651E-04 -6.2154E-04 -4.5013E-04 -6.2154E-04 -5.7601E-04 -6.2078E-04 -4.2343E-04 -6.2078E-04 -5.7524E-04 -6.1998E-04 -4.3869E-04 -6.1998E-04 -5.7443E-04 -6.1936E-04 -4.2343E-04 -6.1936E-04 -5.7380E-04 -6.1902E-04 -4.1962E-04 -6.1902E-04 -5.7345E-04 -5.6615E-04 -4.4250E-04 -5.6615E-04 -5.2070E-04 -5.6702E-04 -4.3297E-04 -5.6702E-04 -5.2156E-04 -5.6821E-04 -4.2725E-04 -5.6821E-04 -5.2274E-04 -5.6960E-04 -4.2343E-04 -5.6960E-04 -5.2411E-04 -5.7094E-04 -4.1962E-04 -5.7094E-04 -5.2545E-04 -5.7196E-04 -4.0817E-04 -5.7196E-04 -5.2646E-04 -5.7246E-04 -4.0817E-04 -5.7246E-04 -5.2695E-04 -5.7237E-04 -3.9673E-04 -5.7237E-04 -5.2685E-04 -5.7179E-04 -3.8910E-04 -5.7179E-04 -5.2626E-04 -5.7093E-04 -3.7384E-04 -5.7093E-04 -5.2538E-04 -5.7003E-04 -3.8147E-04 -5.7003E-04 -5.2448E-04 -5.6935E-04 -3.7384E-04 -5.6935E-04 -5.2379E-04 -5.6903E-04 -3.5858E-04 -5.6903E-04 -5.2346E-04 -5.1605E-04 -3.8528E-04 -5.1605E-04 -4.7059E-04 -5.1687E-04 -3.7766E-04 -5.1687E-04 -4.7141E-04 -5.1817E-04 -3.7384E-04 -5.1817E-04 -4.7270E-04 -5.1972E-04 -3.7575E-04 -5.1972E-04 -4.7423E-04 ————————————————————————————  5. 应力分布求解 得到每个三角形位移之后,我需要求解每个单元的应力情况,这里采用公式进行计算,求出的应力就是三角形单元任意一点的应力,这里需要注意的是,相邻三角形单元的应力值是不连续的。为了将这种应力以图的形式直观展示出来,还需要做一些工作,Matlab中含有一个colorbar功能,我们选择jet形式,这和仿真软件得到的结果形式一致,其他的设置在代码中有详细解释,这里不再赘述,最后,得到的应力分布图如下图5、6所示。(对应程序文件为stress.m)通过图像可以看出,Ansys结果更为漂亮,因为其网格有加密,但是两者的变化趋势几乎一致。 5. 应力分布求解 得到每个三角形位移之后,我需要求解每个单元的应力情况,这里采用公式进行计算,求出的应力就是三角形单元任意一点的应力,这里需要注意的是,相邻三角形单元的应力值是不连续的。为了将这种应力以图的形式直观展示出来,还需要做一些工作,Matlab中含有一个colorbar功能,我们选择jet形式,这和仿真软件得到的结果形式一致,其他的设置在代码中有详细解释,这里不再赘述,最后,得到的应力分布图如下图5、6所示。(对应程序文件为stress.m)通过图像可以看出,Ansys结果更为漂亮,因为其网格有加密,但是两者的变化趋势几乎一致。
function [Fx,Fy,Fxy]=stress(B,Node_information,Element_information,D,U)
Num_element=size(Element_information,1);
Num_node=size(Node_information,1);
Fx=[];
Fy=[];
Fxy=[];
for i = 1:Num_element
Node_num=Element_information(i,2:4);
u=[U(Node_num);U(Node_num+Num_node)];
f=D*B(3*i-2:3*i,:)*u;
Fx=[Fx;f(1)];
Fy=[Fy;f(2)];
Fxy=[Fxy;f(3)];
end
end
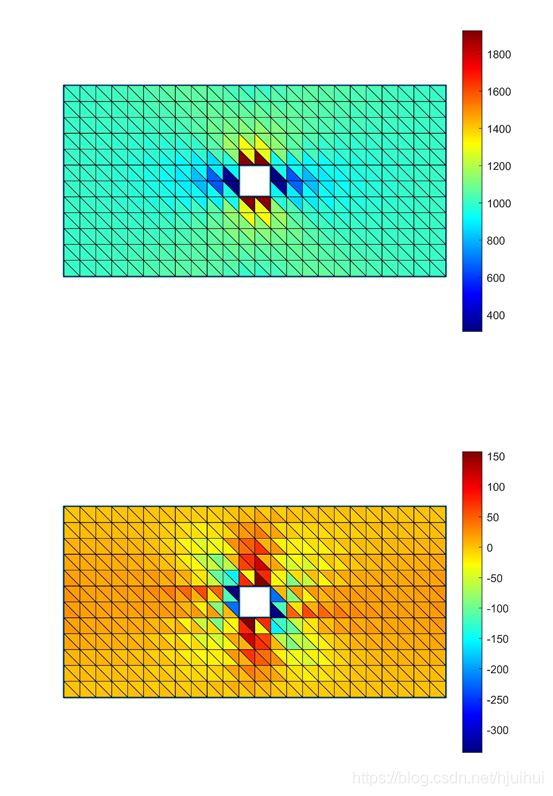 matlab计算 x y 方向应力 matlab计算 x y 方向应力
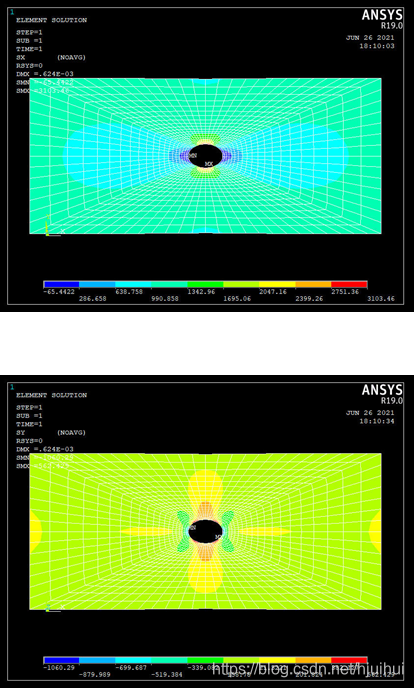 ansys 计算 x y 方向应力 ansys 计算 x y 方向应力
6. 结果分析 凭我自己的直观想象,这个问题的模型对称,荷载对称,得到的应力结果和位移结果都应该是对称的,和我得到的结果显然一致,而且在孔洞处又很明显的应力集中的状态,而且随着网格的加密,其结果会往Ansys得到的结果逼近。所以我编成得到结果很好的和Ansys吻合在了一起。 但是限于自己的水平,代码有的地方比较冗杂繁复,而且计算速度明显低于成熟的商业软件Ansys,我也要继续努力,为了让我们自己的国家也有一套成熟的有限元软件而努力。
|
 1. 模型绘制与网格划分 此问题第一步需要解决的就是网格的划分,模型绘制可以使用Matlab自带的矩形和圆工具,对于网格的划分,以一种较为简单的方式进行,这样也可以减低一些编程难度,效果如图所示,我全部使用三角形单元,对于中间的圆形孔洞,圆形的网格划分在程序上存在一定难度,我用方形空洞代替,在划分网格的同时,对于节点的编号和坐标将其记录在一个Node_information矩阵中,对于三角形单元的编号和包含的节点保存在Element_information中。(此部分对应的程序为Meshing.m)
1. 模型绘制与网格划分 此问题第一步需要解决的就是网格的划分,模型绘制可以使用Matlab自带的矩形和圆工具,对于网格的划分,以一种较为简单的方式进行,这样也可以减低一些编程难度,效果如图所示,我全部使用三角形单元,对于中间的圆形孔洞,圆形的网格划分在程序上存在一定难度,我用方形空洞代替,在划分网格的同时,对于节点的编号和坐标将其记录在一个Node_information矩阵中,对于三角形单元的编号和包含的节点保存在Element_information中。(此部分对应的程序为Meshing.m) 2. 单元刚度矩阵的建立与整体刚度矩阵装配 得到单元信息和节点信息之后,下面的操作类似于桁架的有限元分析,需要建立每一个单元对应的刚度矩阵,对于三角形单元来说,课件中有详细的说明,其核心利用到的公式如下: 下面我们将公式转化为代码语言,D矩阵比较容易书写,B矩阵则要利用上步储存的Node_information和Element_information,通过矩阵的索引准确的找到每个三角形单元对应的节点坐标,再通过矩阵乘法则可以得到每个单元的刚度矩阵(66)。 为了利于后续的装配,我们将每个单元的刚度矩阵赋值到一个‘小装配矩阵’,此矩阵含义为把一个(66)矩阵按照公式1规则装配到一个(2*节点总数)的方阵中,此规则不同于桁架结构,因为其刚度矩阵是按照(u1 u2 u3 v1 v2 v3)的顺序来生成的,对应的匹配规则也要得到调整。(完成此部的程序文件对应为Single_triangular.m)
2. 单元刚度矩阵的建立与整体刚度矩阵装配 得到单元信息和节点信息之后,下面的操作类似于桁架的有限元分析,需要建立每一个单元对应的刚度矩阵,对于三角形单元来说,课件中有详细的说明,其核心利用到的公式如下: 下面我们将公式转化为代码语言,D矩阵比较容易书写,B矩阵则要利用上步储存的Node_information和Element_information,通过矩阵的索引准确的找到每个三角形单元对应的节点坐标,再通过矩阵乘法则可以得到每个单元的刚度矩阵(66)。 为了利于后续的装配,我们将每个单元的刚度矩阵赋值到一个‘小装配矩阵’,此矩阵含义为把一个(66)矩阵按照公式1规则装配到一个(2*节点总数)的方阵中,此规则不同于桁架结构,因为其刚度矩阵是按照(u1 u2 u3 v1 v2 v3)的顺序来生成的,对应的匹配规则也要得到调整。(完成此部的程序文件对应为Single_triangular.m)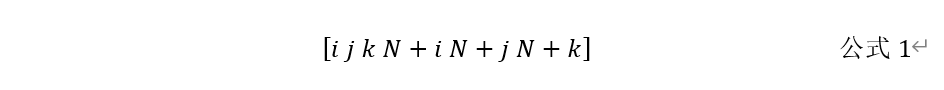 由于得到了‘小装配矩阵’,接下来对每个三角形单元得到的‘小装配矩阵’作累加即可,这里只需要对Element_information遍历即可。完成此部的程序文件对应为Assemble.m)
由于得到了‘小装配矩阵’,接下来对每个三角形单元得到的‘小装配矩阵’作累加即可,这里只需要对Element_information遍历即可。完成此部的程序文件对应为Assemble.m) 4. 求解节点位移 经过上几步的准备工作,已经得到了刚度K矩阵和外载F矩阵,只需要对K求逆再与F相乘就可以得到结果了。但此时存在一个问题,对于刚度矩阵数量较为庞大,很容易出现矩阵接近奇异值的情况,Matlab处理此问题较为强大,提供了四种求逆的方法。如下表所示:
4. 求解节点位移 经过上几步的准备工作,已经得到了刚度K矩阵和外载F矩阵,只需要对K求逆再与F相乘就可以得到结果了。但此时存在一个问题,对于刚度矩阵数量较为庞大,很容易出现矩阵接近奇异值的情况,Matlab处理此问题较为强大,提供了四种求逆的方法。如下表所示: 5. 应力分布求解 得到每个三角形位移之后,我需要求解每个单元的应力情况,这里采用公式进行计算,求出的应力就是三角形单元任意一点的应力,这里需要注意的是,相邻三角形单元的应力值是不连续的。为了将这种应力以图的形式直观展示出来,还需要做一些工作,Matlab中含有一个colorbar功能,我们选择jet形式,这和仿真软件得到的结果形式一致,其他的设置在代码中有详细解释,这里不再赘述,最后,得到的应力分布图如下图5、6所示。(对应程序文件为stress.m)通过图像可以看出,Ansys结果更为漂亮,因为其网格有加密,但是两者的变化趋势几乎一致。
5. 应力分布求解 得到每个三角形位移之后,我需要求解每个单元的应力情况,这里采用公式进行计算,求出的应力就是三角形单元任意一点的应力,这里需要注意的是,相邻三角形单元的应力值是不连续的。为了将这种应力以图的形式直观展示出来,还需要做一些工作,Matlab中含有一个colorbar功能,我们选择jet形式,这和仿真软件得到的结果形式一致,其他的设置在代码中有详细解释,这里不再赘述,最后,得到的应力分布图如下图5、6所示。(对应程序文件为stress.m)通过图像可以看出,Ansys结果更为漂亮,因为其网格有加密,但是两者的变化趋势几乎一致。 matlab计算 x y 方向应力
matlab计算 x y 方向应力 ansys 计算 x y 方向应力
ansys 计算 x y 方向应力